Singular points (or) Singularity of f(z)

SINGULARITIES - RESIDUES RESIDUE THEOREM

(d) Singular points (or) Singularity of f(z)

[A.U. A/M 2011, M/J 2012] [A.U A/M 2019 (R17)]

A point z = z₀ at which a function f (z) fails to be analytic is called a singular point or singularity of f (z).

Example : Consider f (z) = 1 / 2 - 3

Here, z = 3 is a singular point of f (z)

1. Types of singularities

(e) Isolated singularity:

A point z = zo is said to be isolated singularity of f (z)

if (i) f (z) is not analytic at z = z₀

(ii) There exists a neighbourhood of z = z₀ containing no other singularity.

Example : ƒ (z) = 1/z

This function is analytic everywhere except at z = 0

.. z = 0 is an isolated singularity.

Note: If z = zo is an isolated singular point of a function f (z), then the singularity is called

(i) a removable singularity (or)

(ii) a pole (or)

(iii) an essential singularity

according as the Laurent's series about

z = z₀ of f (z), valid in a deleted neighbourhood of z = z₀, has

(i) no negative powers or

 (ii) a finite number of negative powers or

(iii) an infinite number of negative powers

Note 2: Let, z = z₀ be an isolated singular point of the function f (z).

Then, f (z) is analytic inside and on a circle C except at z = z₀

the centre of C and therefore f (z) can be expanded by a Laurent's series.

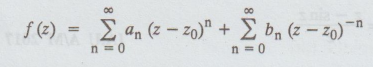
 (f) Removable singularity

If the principal part of f (z) contains no term

i.e., b = 0 for all n, then the singularity z = z₀ is known as the removable singularity of f (z).

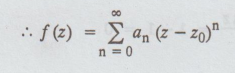
A singular point z = z₀ is called a removable singularity of f (z), if lim(z → z0) f z  exists finitely

Example 4.3.6. (a) What is the nature of the singularity z = 0 of the function f(z) = sin z –z / z³

 [Anna, May 2001, May 1999] [A.U April 2017 R-15, U.D]

Solution:

Given: ƒ (z) = sin z - z / z³

The function f(z) is not defined at z = 0.

But by L' Hospital's rule.

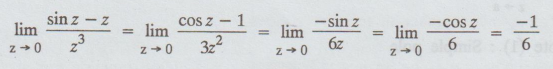
Since, the limit exists and is finite, the singularity at z = 0 is a removable singularity.

Example 4.3.6 (b) Classify the singularities for the functions

f(z) = z  - sin z / z

Solution:

Given:  f(z) = z  - sin z / z

The function f(z) is not defined at z = 0.

But by L'Hospital rule.

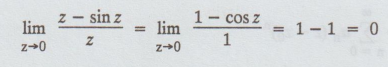
Since, the limit exists and is finite, the singularity at z = 0 is a removable singularity.

Example 4.3.7. Find the nature of the singularity at z = 0 of f (z) = sin z / z

Solution: Given: g (z) = sin z / z

The function f (z) is not defined at z = 0

But by L' Hospital's rule

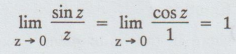
Since, the limit exists and is finite, the singularity at z = 0 is a removable singularity.

(g) Poles

If we can find a positive integer n such that 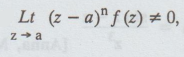then z = a is called a pole of order n for f (z).

 (or)

An analytic function f (z) with a singularity at z = a if

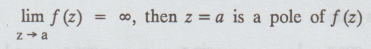
Note (1) : Simple pole

A pole of order one is called a simple pole.

Example: If f (z) = 1 / (z - 4)² (z - 3)³ (z - 1)

Here, z = 1 is a simple pole

z = 3 is a pole of order 3

z = 4 is a pole of order 2

 (h) Essential singularity

[A.U D15/J16 R-08, R-13]

If the principal part contains an infinite number of non zero terms, then z = z₀ is known as an essential singularity.

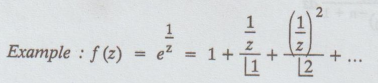
has z = 0 as an essential singularity

Since, f (z) is an infinite series of negative powers of z.

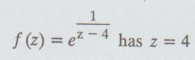 has z = 4 as an essential singularity.

Note: The removable singularity and the poles are isolated singularities. But, the essential singularity is either an isolated or non-isolated singularity.

(i) Entire function (or) Integral function :

A function f (z) which is analytic everywhere in the finite plane (except at infinity) is called an entire function or an integral function.

Example: e^z, sinz, cos z are all entire functions.

(j) Meromorphic function

A function f (z) which is analytic everywhere in the finite plane except at finite number of poles is called a meromorphic function.

Example:

f(z) = z + 3 / (z-1) (z-2)² is called a Meromorphic function, since it fails to be analytic only at poles z = 2 and z = 1.

II Residues

(k) Residues

If z = z₀ is an isolated singular point of f (z), we can find the Laurent's series of f(z) about z = z₀

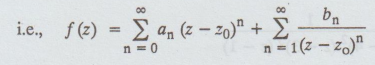
The co-efficient of 1 / z - z₀ in the above expansion is called the residue of f (z) at z = z₀

i.e., b₁ is the residue of f (z) at z = z₀

From the definition of b, given in the theorem of Laurent's series

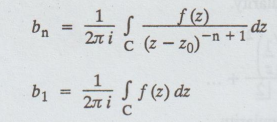
Residue of f (z) at z = z₀ may be denoted by Res [f(z), z₀]

Evaluation of Residues

(i) Residue at a pole of order m.(z) =

If z = z₀ is a pole of order m, a simple formula to determine the residue is given by

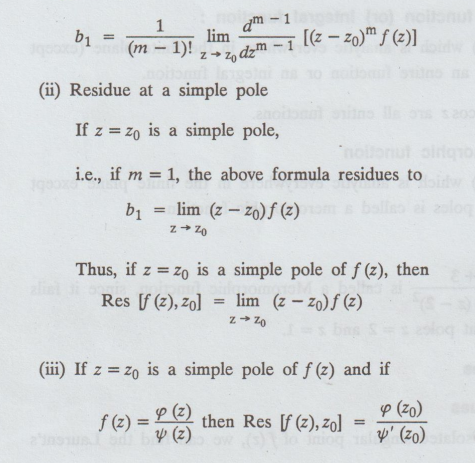
Note :

1. If the singularities are poles, we can use the above formulae to evaluate the residues of f (z). Otherwise, expand the function in Laurent's series and then find the residues.

2. If f (z) has a removable singularity at zo, then Res [f(z), zo]

3. Limit point of poles is a non-isolated essential singularity.

4. Limit point of zero is an isolated essential singularity.