Singularities - residues residue theorem: Solved Example Problems

Example 4.3.8. Find the kind of singularity of the function cot л z / (z - a)²

Solution

 

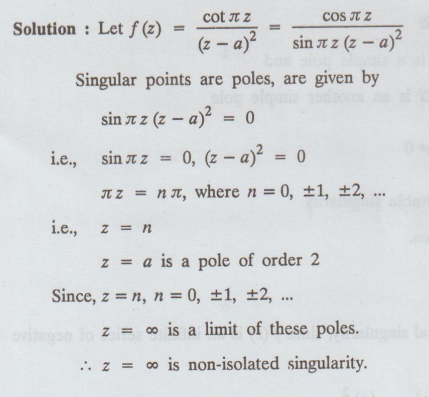
Example 4.3.9. Classify the singularity of f(z) = e^1/z / (z – a)²  [Anna, May 2001]

Solution: Poles f f (z) are obtained by equating the denominator to zero.

i.e., (z - a)² = 0

z = a is a pole of order 2

Now, zeros of f (z)

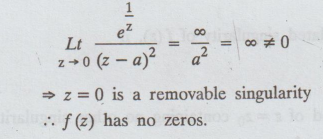
Example 4.3.10. Classify the nature of singularities of the functions e^z / z² + 4 and e^1/z.

 [Anna, May 2001]

Solution:

(i) Let f (z) = e^z / z² + 4

The poles of f (z) are obtained by equating the denominator to zero.

i.e., z² + 4 = 0

z² = -

z =  ±2i

z = 2i is a simple pole and

z = -2i is an another simple pole

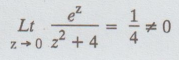
z = 0 is a removable singularity

f (z) has no zeros.

(ii) Let, f (z) = e^1/z

z = 0 as an essential singularity, since f (z) is an infinite series of negative power of z.

 

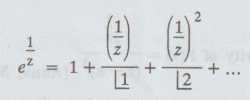
Example 4.3.11. Classify the various types of singularities and give one example for each type.

[Anna, Nov. 1996]

Solution :

(i) Isolated singularity

A point z = z₀ is said to be isolated singularity of f (z), if

(i) f (z) is not analytic at z = z₀

(ii) There exists a neighbourhood of z = z₀ containing no other singularity.

Example : f(z) = 1 / z

This function is analytic everywhere except at z = 0

.z = 0 is an isolated singularity.

(ii) Removable singularity

A singular point z = z₀ is called a removable singularity of f (z), if  exists finitely.

Example: f(z) = sin z / z

(iii) Poles

If we can find a positive integer n such that

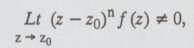 then z = z₀ is called a pole of order n for f (z).

Example : f (z) = 1 / (z - 4)² (z - 3)⁴

Here, z = 4 is a pole of order 2

z = 3 is a pole of order 4

(iv) Essential singularity

[A.U D15/J16 R-13]

If the principal part contains an infinite number of terms, then z = zo is known as an essential singularity.

Example: f(z) = e^1/z

 

Example 4.3.12. (a) Find the singular point of f (z) = sin 1 / z – a.  State the nature of singularity.

Solution: z = a is the only singular point in the finite plane.

sin 1 / z – a = 1 / z – a – 1 / 3!(z - ɑ)³ + 1 / 5!(z - ɑ)⁵ - …

z = ɑ is an essential singularity

It is an isolated singularity

 

Example 4.3.12. (b) Identify the type of singularity of function sin ( 1 / 1 – z) [A.U A/M 2015 R-13]

Solution : z = 1 is the only singular point in the finite plane.

z = 1 is an essential singularity.

It is an isolated singularity.

 

Example 4.3.13. Find the singular points of f (z) = 1 / (sin 1 / z - ɑ) ,state their nature.

 [A.U M/J 2007]

Solution: f (z) has an infinite number of poles which are given by

1 / z - ɑ = nπ , n = ±1, ±2, …

i.e., z - ɑ = 1 / nπ; z = ɑ + 1 / nπ

But, z = ɑ is also a singular point.

It is an essential singularity.

It is a limit point of the poles.

So, it is a non-isolated singularity.

 

Example 4.3.14. Find the singularities of f (z) = sin ( 1 / z + 1 )

Solution: Given: f (z) = sin (1 / z + 1)

z = -1 is an essential singularity of f (z).

 

Example 4.3.15. Find the residue of 1 – e^2z  at z = 0

[A.U. M/J 2013]

Solution:

 

Example 4.3.16(a) Classify the singularity of f (z) = tan z / z

Solution:

 

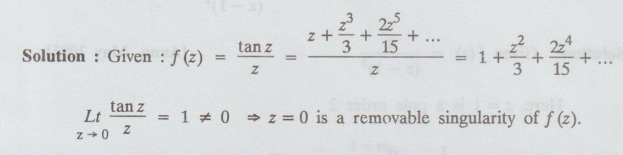
Example 4.3.16(b) Evaluate the residue of f (z) = tan z = at its singularities.  [AU M/J 2016 R-13]

Solution :

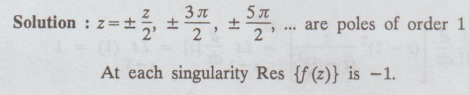
Example 4.3.16 (c) Find the residue of f (z) = tan z at z = π / 2

Solution :

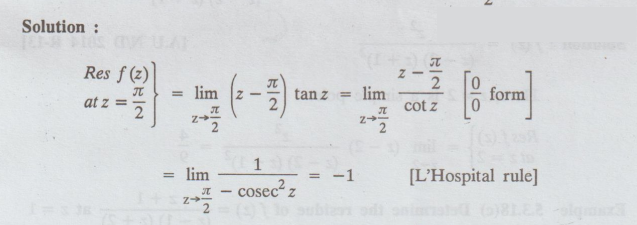
Example 4.3.17. Find the residue of f (z) = 1 - e-^z / z³ at z = 0

Solution:

 

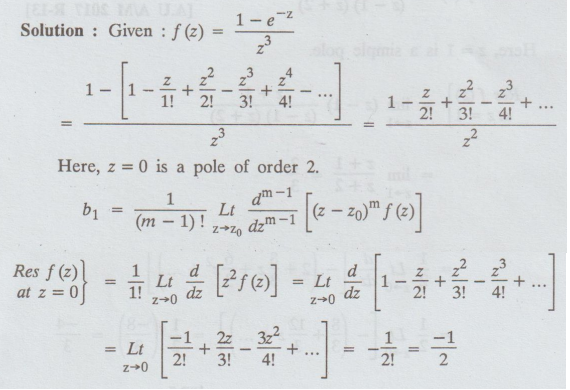
Example 4.3.18(a) Find the residue of f (z) = z / ( z – 1 )² at its pole. [Anna, May 2002]

Solution:

 

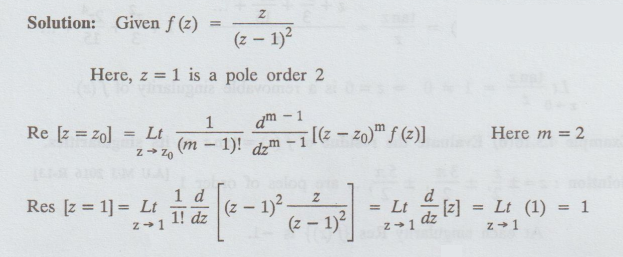
Example 4.3.18(b) Find the residue of ƒ (z) = z² / (z - 2) (z + 1)² at z = 2[A.U N/D 2014 R-13]

Solution :

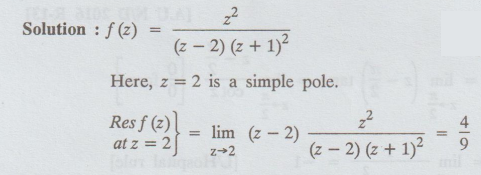
Example 4.3.18(c) Determine the residue of f (z) = z + 1 / ( z- 1) (z + 2) at z = 1

Solution:

 

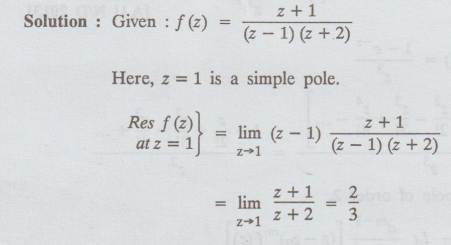
Example 4.3.19. Calculate the residue of f (z) = e^2z / (z+1)² at its pole.

[Anna, May 2001, J/F 2008, N/D 2009, N/D 2011]

Solution :

 

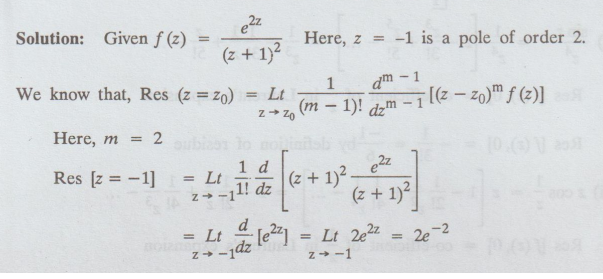
Example 4.3.20. If f (z) = - 1 / z – 1 -2 (1 + (z − 1) + (z - 1)² + ...],  find the residue of f(z) at z = 1. [A.U. M/J 2010, N/D 2010, N/D 2012]

Solution: The residue of f (z) at z = 1 is equal to the co-efficient of 1 / z – 1 in the Laurent's series of f (z) about z = 1 that is equal to -1.

 

Example 4.3.21. Find the residue of cot z at z = 0.

Solution:

 

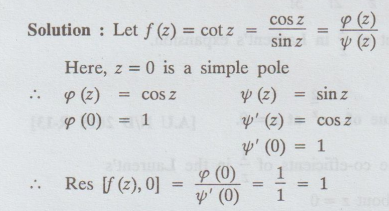
Example 4.3.22. Find the residues at z = 0 of the functions

(i) f (z) = e^l/z (ii) f (z) = sin z / z⁴ [A.U A/M 2004] (iii) f (z) = z cos 1 / z

Solution: The residues are the co-efficients of 1/z in the Laurent's expansions of f (z) about z = 0.

Example 4.3.23. Find the residue of f (z) = 1 / z^e e^z

Solution :

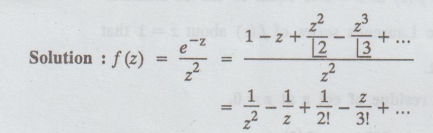
Res [f (z), 0] = co-efficient of 1/z in Laurent's expansion.

Res [f (z), 0] = -1

 

Example 4.3.24. Find the residue of z e^2/z at z = 0.

[A.U N/D 2015 R-13]

Solution: The residues are the co-efficients of 1/z in the Laurent's expansion of f (z) about z = 0

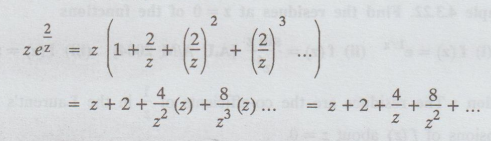
Res [f (2), 0] = Co-efficient of 1/z in Laurent's expansion.

Res [f(z), 0] = 4 by definition of residue.

 

Example 4.3.25. Calculate the residues of the function f(z) = z sin z / (z - π)³ at z = π.

Solution:

 

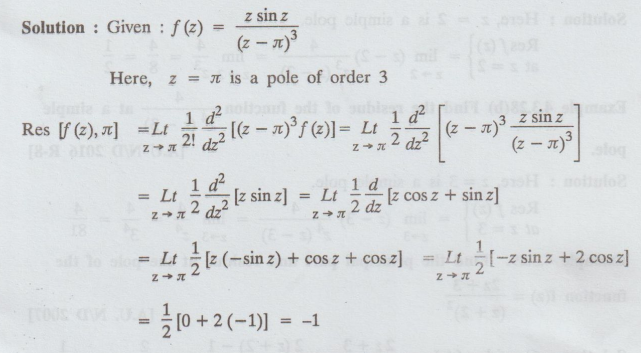
Example 4.3.26. Find the residue of z2 sin (1/z) at z = 0

Solution:

 

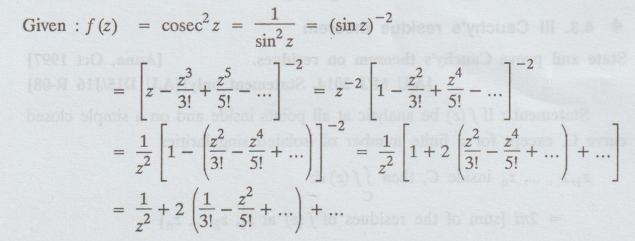
Example 4.3.27. Find the residue of the function f(z) = cosec² z at z = 0.

Solution :

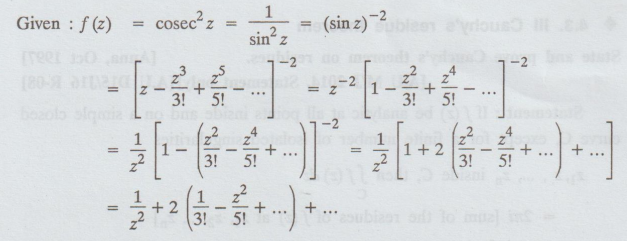
Res [f(z), 0] = co-efficient of 1/z in the Laurent's series expansion = 0

 

Example 4.3.28 (a) Find the residue of the function f(z) = 4 / z³(z – 2) simple pole.

Solution:

 

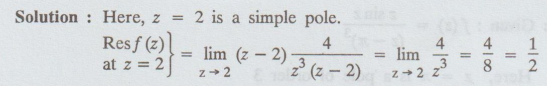
Example 4.3.28(b) Find the residue of the function 4 / z⁴ (z – 3) at a simple pole.

[A.U N/D 2016 R-8]

Solution:

Here, z = 3 is a simple pole.

 

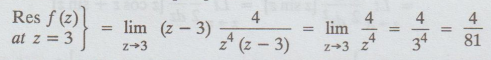
Example 4.3.29. Find the principal part and residue at the pole of the function f(z) = 2z + 3 / (z + 2)²

[A.U. N/D 2007]

Solution

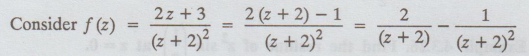
which is the required principal part of f (z)

Residue at the pole z = -2 (double pole) is the coefficient of 1 / z + 2

which is equal to 2.

 

Example 4.3.30. Identify the type of singularities of the following function:

f (z) = e^{(1/(z − 1))} [A.U N/D 2009]

Solution: