Sinusoidal voltages and currents

SINUSOIDAL VOLTAGES AND CURRENTS

Voltages and currents varying as sine functions of time find more practical use. Hence, the rest of this topic will be devoted to the study of AC sinusoidal quantities. It is also well known that any periodic source (with an arbitrary form) can be represented by an equivalent combination of sinusoidal sources (Fourier series).

A sinusoidal voltage and current can be represented as

e = E_m sin at or v = V_m sin wt and

i = I_m sin wt

where e or v and i are instantaneous values and E_m or V_m and I_m are peak values. The symbol of 'w' stands for angular frequency in radians per second.

v = V_m sin (2лf) t

i = I_m sin (2 π f) t

w = 2πf

f = w / 2π = 1 / T

where ‘f’ is the frequency in cycles per second (Hz)

 

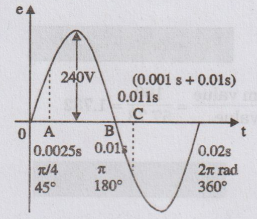
EXAMPLE 17: A sinusoidal voltage of frequency 50 Hz has a maximum value of 240 V. What is its equation? Find the value of the voltage at (a) time t = 0.0025 s after the voltage passes through zero and is increasing and at (b) time t = 0.001 s after the voltage passes through zero and is decreasing.

Solution :

The equation is

v = V_msin 2πft = 240 sin 2π × 50 × t

= 240 sin 314t Volts

(a) At time t = 0.0025 s after the voltage passes through zero and is increasing means the voltage is passing through A.

At A, v = 240 sin (314 × 0.0025)

This value (314 × 0.0025) is converted into degree i.e.,

(314 × 0.0025 × 180 / π = 45° )

v = 240 sin 45°

(b) At time, t = 0.001 s after the voltage passes through zero and is decreasing implies at C (i.e. 0.001 s after B) i.e. at t = 0.011 s.

At C, v = 240 sin (314 × 0.011)

Once again 314 × 0.011 is in radians; the radian value is converted into degree

i.e., 3.454 × 180/ π = 197.8°

U = 240 sin 197.8°

 

EXAMPLE 18: A 50 Hz sinusoidal current wave has a peak amplitude of 10 A. Find the rate of change of current in amperes per second at time t (a) 0.0025 (6) 0.005 and (c) 0.01 s after i=0 and is increasing.

Solution:

 

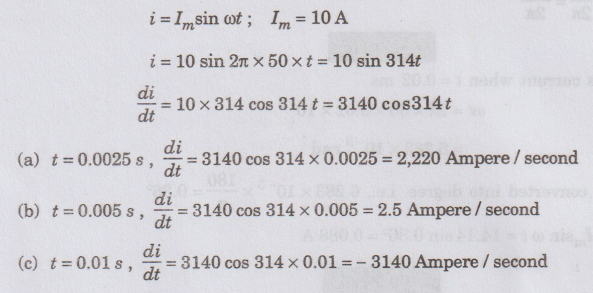
EXAMPLE 19: An alternating current of frequency 60 Hz has a maximum value of 120 A. Write down the equation for its instantaneous value.

Solution:

f = 60 Hz

I_m = 120 A

i = I_m sin wt

w = 2лf = 2π × 60 = 377 rad/s

i = 120 sin 377 t

 

EXAMPLE 20: An alternating current is expressed as i = 14.14 sin 314 t. Determine rms current, frequency and instantaneous current when t = 0.02 ms.

Solution:

i = 14.14 sin 314t

i = I_m sin wt

I_m = 14:14 A

W = 2πf = 314 rad/sec

(i) RMS current I = I_m / √2 = 14.14 / √2

I = 10 A

(ii) Frequency f= ω / 2π = 314 / 2π

f = 50 Hz

(iii) Instantaneous current when t = 0.02 ms

wt = 2π × 50 × 0.02 × 10^-3

= 6.283 × 10^-3 rad

This value is converted into degree. i.e., 6.283 × 10^-3 × 180 / π = 0.36°

i = I_m sin wt = 14.14 sin 0.36° = 0.088 A

i = 0.088 A