Small Signal Parameters of MOSFET

Small Signal Parameters

• The time-varying signal source in Fig. 7.1.1 (a) generates a time-varying component of the gate-to-source voltage.

• The instantaneous gate-to-source voltage is given by,

V_GS = V_GSQ + V_i = V_GSQ + V_gs (7.2.1)

Where V_GSQ is the d.c. component and VgS is the a.c. component.

• The instantaneous drain current is,

I_D =  K(V_GS - V_T)²    ...(7.2.2)

• Substituting equation (7.2.1) into equation (7.2.2) we have,

• The first term in equation (7.2.3(b)) represents the d.c. or quiescent drain current Ipo, the second term represents the time-varying drain current component that is linearly related to the signal vgs, and the third term is proportional to the square of the signal voltage.

• For a sinusoidal input signal, the squared term produces undesirable harmonics, or nonlinear distortion, in the output voltage. To minimize these harmonics, we must have

V_gs << 2 (V_GSQ - V_T) ...(7.2.4)

• Which means that the third term in equation (7.2.3(b)) should be much smaller than the second term. • Equation (7.2.4) represents the small signal condition that must be satisfied for linear amplifiers.

• Neglecting the vas term, we can write equation (7.2.3(b)) as

i_D = I_DQ + i_d

where,

I_DQ == K(V_GSQ - V_T)² … d.c. component and

i_d = 2K (V_GSQ - V_T) V_gs  … a.c. components

•  The small signal drain current is related to the small signal gate-to-source voltage by the transconductance gm. The relationship is given by,

gm = I_d / V_gs = 2K (V_GSQ - V_T) ...(7.2.6)

• The transconductance can also be obtained from the derivative,

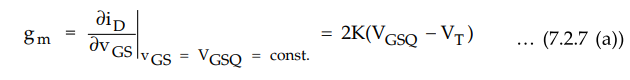
which can be written

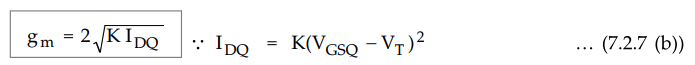
• The transconductance is a ratio of output current to input voltage and hence it represents the gain of the MOSFET.

• The Fig. 7.2.1 shows the drain current versus gate-to-source voltage characteristics for the MOSFET biased in the saturation region.

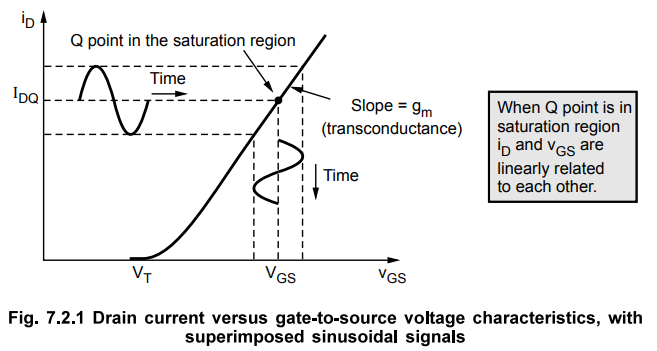
• The transconductance gm is the slope of the curve.

• If the time-varying signal Vgs is sufficiently small, the transconductance g is a constant.

• With the Q-point in the saturation region, the MOSFET operates as a current source that is linearly controlled by VgS.

• If the Q-point moves into the nonsaturation region, the MOSFET no longer operates as a linearly controlled current source.

• As shown in equation 7.2.7  (a), the transconductance is directly proportional to the conduction parameter K, which in turn is a function of the width-to-length ratio. Therefore, increasing the width of the MOSFET increases the transconductance, or gain, of the MOSFET.

Ex. 7.2.1 Calculate the transconductance of a MOSFET having following parameters :      VT = IV, 1/2µ_nC_ox = 30 µA/V² and W/L = 50. Assume the drain current, ID = 1.2 mA.

Sol.:

K = (1/2µ_nC_ox ) (W/L)

= 30 × 50 µA/V² = 1.5 mA/ V²

Assuming MOSFET is biased in the saturation region we have,

g_m = 2 √K I_DQ = 2√(1.5) (1.2)

= 2.68 mA/V

Important Concept

The transconductance of a bipolar transistor is given by gm = ICQ/V_T For I_DQ = 1.2 mA, the gm = 1.2 mA/0.026 V = 46.15 mAJV, which is quite higher in comparison with the transconductance value of MOSFET. In general, transconductance of MOSFET and hence the gain are smaller compared to those of BJTs. This is the disadvantage of MOSFETs over BJTs.

Review Question

1. Explain the small signal parameters of MOSFET.