Solved problems on kirchoff's laws

SOLVED PROBLEMS ON KIRCHOFF'S LAWS

Example 1 Find the current through 3 Ω resistor in the circuit shown.

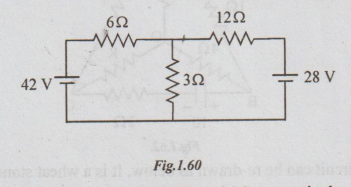
Solution: Let I₁ and I₂ be the currents through 6Ω and 3Ω respectively.

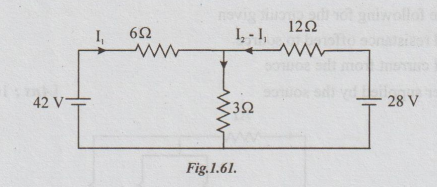
Then, by KCL the current through

12 Ω = I₂ - I₁

Applying KVL to the left loop we get

42-6I₁-3I₂ = 0

⇒ 6I₁ +3I₂ = 42

or 2I₁+ I₂ = I₄... (a)

Similarly applying KVL to the right loop,

12 (I₂-I₁)-28 +3I₂  = 0

=> - 12I₁ + I51₂ = 28

⇒ -2I₁ +2.5 I₂ = 28/6 = 4.67...(b)

Adding (a) and (b)

3.5I₂ = 18.67

 I₂ = -5.33 A

Ans: Current through 3 Ω = 5.33 A

Note: Unless stated otherwise, go round the loop in clockwise direction.

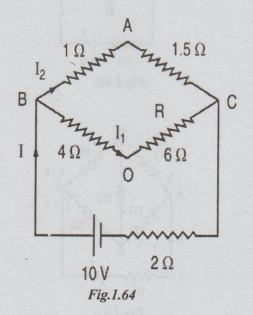
Example 2 Find the value of R and the current flowing through it in the circuit shown when the current in the branch OA is zero. A

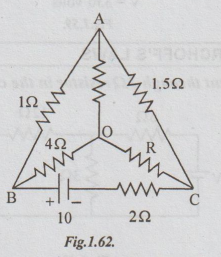
Solution: The given circuit can be re-drawn as below. It is a wheat stone bridge.

As the current through the branch OA is zero, the bridge is said to be under balanced condition. Then product of resistances of opposite arms must be equal.

 1 × R = 4 × 1.5

⇒ R = 6 Ω

When the current through OA is zero, remove OA.

Then the circuit becomes as

2.5 and 10 are in parallel. Total resistance of the circuit

R_T =  2.5 × 10/ 2.5 + 10 + 2 = 2 + 2 = 4 Ω

 Source current I_S = V/R_T = 10/4

I_S = 2.5A

I_S is divided into two paths.

By division of current formula I₁=I_SR₂/R₁+R₂

= 2.5 × 2.5/10 + 2.5 = 0.5A

Current through R = 0.5 A

Ans: R =6 Ω, I₆ = 0.5 A

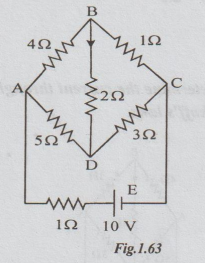
Example 3 In the circuit shown, determine the current through the 2 Ω resistor and the total current delivered by the battery. Use Kirchoff's laws.

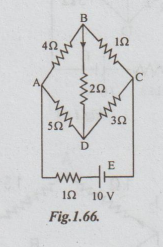
Solution:

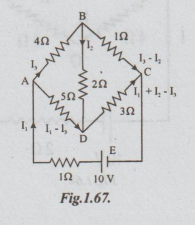
Let  I₁ = current from the battery

I₂ = current through 2 Ω

I₃ = current through 4 Ω

The currents in other resistors are obtained by applying KCL at nodes A, B and C. By applying KCL at D, we can check the expressions.

Applying KVL to the loop ABDA,

Ans: I₁ = 2.49 A, I₂ = 0.281 A from D to B.

Example 4 Obtain the potential difference Vxy in the circuit shown in the fig1.68.

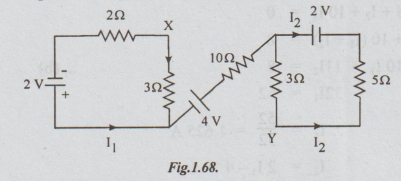
Solution: As 4 V source does not have return path, there is no current from 4 volts. Applying Ohm's law, to left and right loop to get,

I₁= 2/2+3= 0.4

I₂= 2/3+5 = 0.25 A

V_XY = p.d. between X and Y

= 3I₁ + 4-3I₂

= 3 × 0.4 + 4-3 × 0.25 = 5.2-0.75

= 4.45 volts with y + ve

Example 5 Two batteries A and B are connected in parallel and a load of 10 Ω is connected across their terminals. A has an emf of 12 V and internal resistance (I.R) of 2 Ω B has an emf of 8 volts and I.R of 1 Ω Using Kirchoff's laws, determine the values and directions of currents in each of the batteries and in external resistance. Also determine the potential across the external load.

Note: When the statements are given (instead of circuit) the reader must be careful in drawing the circuit correctly.

Batteries are said to be in parallel if terminals of same polarities are joined together.

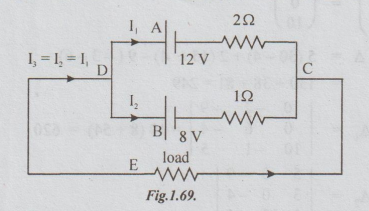
The circuit is shown in the figure 1.69

Let the currents in the batteries be as indicated in the figure.

By KCL, the current through

10 Ω = I₃ = I₁ +I₂

Applying KVL to the loop DACBD.

- 12 + 2I₁ - I₂ + 8 = 0

or 2I₁ - I₂ = 4....(1)

Applying KVL to the loop DBCED, we get

-8 + I₂ + 10 I₃ = 0

⇒ I₂ + 10 (I₁ + I₂) = 8

10 I₁ + 11I₂ = 8....(b)

 (a) × 11+ (b) ⇒ 32I₁ = 52

 I₁ = 52/32 =1.625 A

From equation (a),

I₂ = 2I₁-4

= 2 (1.625)-4 = -0.75 A

I₃ = I₁ + I₂ = 1.625-0.75 = 0.875

p.d. across the load = V₁₀ = I₃ × 10

= 0.875× 10 = 8.75 V

with D at +ve and C at -ve.

Ans: I₁ = 1.625 A; I₂ = -0.75 A; I₃ = 0.875 A; V₁₀ = 8.75 V

Example 6 A network of resistors has a pair of input terminals AB connected to a d.c. supply and a pair of output terminal CD connected to a load resistor of 602 The resistances of the network are AC = BD = 90 Ω, AD = BC = 40 Ω Find the ratio of the current in the load resistor to that taken from supply.

Solution: The network is drawn below. Let V be the supply voltage connected between the input terminals A and B.

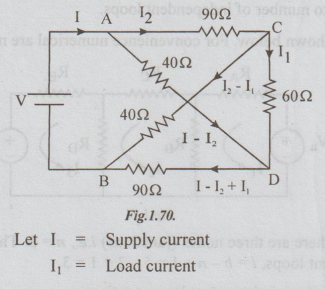
It is required to find I₁/I

Let the current through branch AC be I₂. The other branch currents are expressed by applying KCL.

Applying KVL to the loop ACDA, we get

Minus sign indicates that the direction of I₁ is from the terminal D to C and not from C to D.

I₁/I = 0.2

Or I₁ = 0.21 = 20% of 1