Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Solving AC circuits by loop current methods
Electric Circuit Analysis: Unit I: Basic circuits analysis : Solving AC circuits by loop current methods
Solving AC circuits
by loop current methods
[Very Important Note: The student should be thorough with the conversion of rectangular to polar and vice versa before he solves the problems on A.C. He can refer the introduction pages for help]
Example 6 Apply mesh current method and determine currents through the resistors of the network shown in fig.1.79.
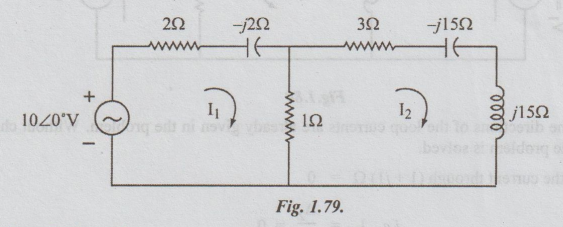
Solution: By inspection,
[Hint: The student is advised to solve the problem by simplification of series parallel combination of impedances.]
Example 7 In the network shown in figure find V2 such that the current in the (1+j1) Ω branch is zero.
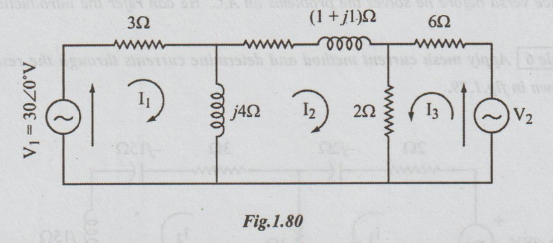
Solution: The directions of the loop currents are already given in the problem. Without changing the directions, the problem is solved.
Given that, the current through (1+j1) Ω = 0
i.e., I2 = ∆2/ ∆ =0
Hence, ∆2 = 0
= 96 < 37° volts In the matrix form, we get the loop
equation as below
Example 8 In the network shown in figure determine V2 such that the current in the 2+ j3 impedance is zero.
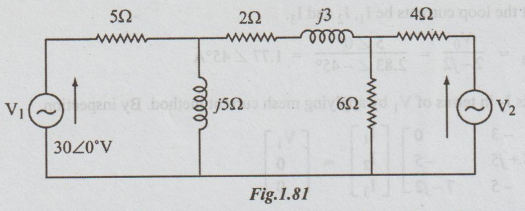
Solution: The directions of the loop currents here are not given. Hence, let us assume that they are all clockwise. Since the current through (2 + j3) is given to be zero, I2 = 0 => ∆2/ ∆=0 Hence the condition
Δ2=0, So, by inspection
Example 9 In the network shown in the figure the source V1 results in a voltage V0 across the (2-j2)Ω impedance. Find the source V1 which corresponds to V0=5<0° volts.
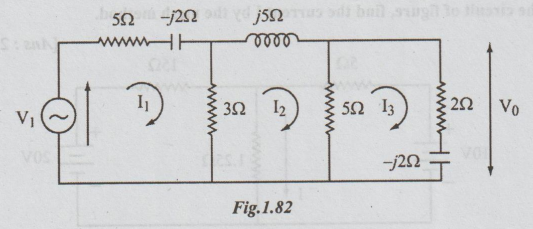
Solution: Let the loop currents be I1, 12 and I3.
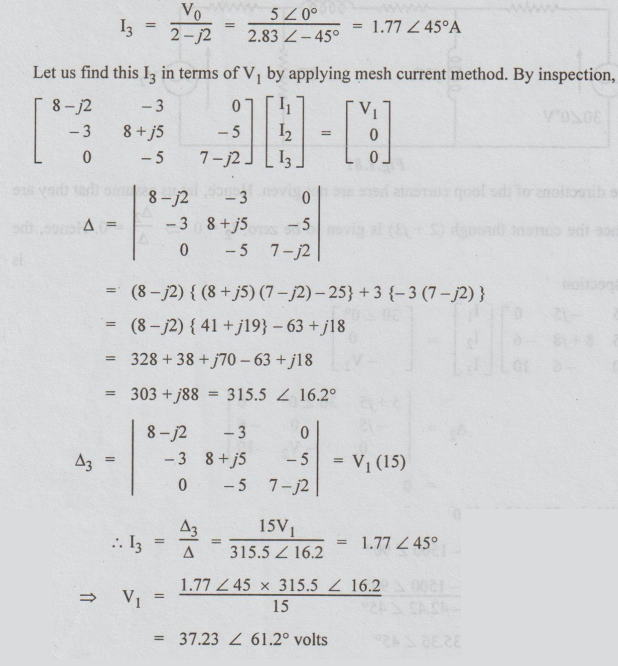
Electric Circuit Analysis: Unit I: b. Basic circuits analysis : Tag: : - Solving AC circuits by loop current methods
Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation