Probability and complex function: Unit I: Probability and random variables
Some important terms of probability
In the study of probability, any process of observation is referred to as an experiment. The results of an observation are called the outcomes of the experiment.
SOME IMPORTANT TERMS OF PROBABILITY
1.
Deterministic experiments
There
are experiments, which always produce the same result, i.e., unique outcome or
unique events, Such experiments are known as deterministic.
2.
Random experiments
The
experiments which do not produce the same result or outcome on every trial are
called Random experiments.
Example
1.
Throw an unbiased die
2.
If we toss a uniform unbiased coin.
Note:
Outcome
In
the study of probability, any process of observation is referred to as an
experiment. The results of an observation are called the outcomes of the
experiment.
3.
Trial and Event
The
performance of a random experiment is called a Trial and the outcome is called
an event.
Example:
Throwing of a coin is a trial and getting H or T is an event.
4.
Sample space
The
totality of the possible outcomes of a random experiment is called the sample
space of the experiment and it will be denoted by 2 (Greek alphabet) or S
(English alphabet)
Each
outcome or element of this sample space is known as the sample point or event
and it is denoted by Greek alphabet ω.
The
number of sample points in a sample space is generally denoted by n (s)
Example
:
1.
Tossing a coin S = {H, T}; n (s) = 2
2.
Tossing two coins simultaneously
S
= {HH, HT, TH, TT}; n (s) = 4
3.
Rolling a die S = {1, 2, 3, 4, 5, 6}; n (s) 6
5.
Finite sample space
If
the set of all possible outcomes of the experiment is finite, then the
associated sample space is a finite sample space.
Example
:
1.
One dimensional sample space

2.
Two dimensional sample space
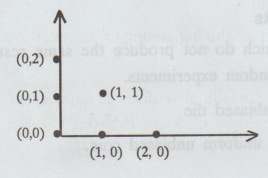
6.
Countably infinite
A
sample space, where the set of all outcomes can be put into a one-to-one
correspondence with the natural numbers, is said to be countably infinite.
7.
Countable or a discrete sample space.
If
a sample space is either finite or countably infinite, we say that it is a
countable or a discrete sample space.
8.
Continuous
If
the elements (points) of a sample space constitute a continuem, such as all the
points on a line, all the points on a line segment, all the points in a plane,
then the sample space is said to be continuous.
9.
Equally likely events
The
possibilities or events are said to be equally likely when we have no reason to
expect any one rather than the other.
Example
In
tossing an unbiased coin, the head or tail are equally likely.
10.
Mutually exclusive events [Disjoint events]
Two
events A and B are said to be mutually exclusive events or disjoint events
provided A ∩ B is the null set.
Note:
If A and B are mutually exclusive, then it is not possible for both events to
occur on the same trial.
Example:
In the throw of a single dice, the events of getting 1, 2, 3,... 6 are mutually
exclusive.
11.
Exhaustive events
Events
are said to be exhaustive when they include all possibilities. on
Example:
In tossing a coin, either the head or tail turns up. There is no other
possiblity and therefore these are the exhaustive events.
12.
Favourable events
The
trials which entail the happening of an event are said to be favourable to the
event.
Example:
In the tossing of a die, the number of favourable events to the appearance of a
multiple of 3 are two (i.e.,) 3 and 6.
14.
Mathematical (or a priori) definition of probability.
If
there are n exhaustive, mutually exclusive and equally likely events,
probability of the happening of A is defined as the ratio m/n, m is favourable
to A.
Thus
probability is a concept which measures numerically the degree of certainty or
uncertainty of the occurrence of an event.
Notation:
p (A) = p = m/n = Favourable number of cases / Exhaustive number of cases
This
gives the numerical measure of probability. Clearly, p is a positive number not
greater than unity.
So
that 0 ≤ p ≤ 1.
Since
the number of cases in which the event A will not happen is n-m, the
probability q that the event A will not happen is given by
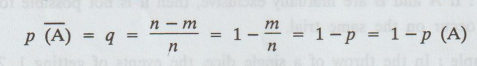
so
that 1, 0 ≤ q ≤ 1.
Note:
An event A is certain to happen if all the trials are favourable to it and then
the probability of its happening is united, while if it is certain not to
happen, its probability is zero. Thus if p = 0, then the event is an
impossible event while if p = 1, the event is certain.
15.
Permutation
Permutation
means selection and arrangement of factors.
Notation:
npr (or) p (n, r) (or) Pn, r (or) prn (or)
(n)r.
The
value of npr is equal to the number of ways of filling places with 'n' things.
npr
= n! / (n − r)!
16.
Permutations with Repetitions
Let
p (n; n1, n2, … nr) denotes the number of
permutations of n objects of which n1 are alike, n2 are
alike, nr are alike,
p
(n: n1 , n2, ..., nr) = n! / n1 ! n2
!... nr!
Example:
The number of permutations of the word 'RADAR' is 5! / 2! 2! = 30
Since
there are five letters of which two are 'R' and the two are 'A'.
17.
Rule of Sum
If
an event can occur in m ways and another event can occur in 'n' ways there are
m + n ways in which exactly one event can occur.
Example:
Consider a box containing 8 red balls and 5 green balls, then are 8+ 5 ways to
choose either red ball or a green ball.
18.
Rule of product
If
there are m outcomes for event E, and n possible outcomes for event E2
then there are mn outcomes for the composite event E1 E2.
Example:
When a pair of dice is thrown once, the number of possible outcomes are 6 × 6 =
36. Since each dice has 6 possible outcomes.
19.
Combination
Combinations
means selection of factors.
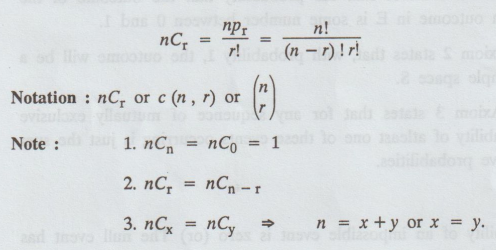
20.
Statistical or Empirical probability
If
in n trials an event E happen m times, then the probability p of the happening
of E is given by
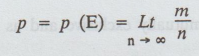
Probability and complex function: Unit I: Probability and random variables : Tag: : - Some important terms of probability
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
