Some standard transformation

Some standard transformation

1. Translation :

The transformation w = C + z, where C is a complex constant, represents a translation.

Let z = x + iy

w = u + iv

 and C = a + ib

Given W = z + C

i.e., u + iv = x + iy + a + ib

u + iv = (x + a) + i(y + b)

Equating the real and imaginary parts, we get

u = x+a, v = y +b

These two equations may be called the transformation equations. vi

Hence the image of any point p (x, y) in the z-plane is mapped onto the point p '(x+a, y + b) in the w-plane. Similarly every point in the z-plane is mapped onto the w plane.

If we assume that the w-plane is super imposed on the z-plane, we observe that the point (x, y) and hence any figure is shifted by a distance |C| = √a2+b2 in the direction of C i.e., translated by the vector representing C.

Hence this transformation transforms a circle into an equal circle. Also the corresponding regions in the z and w planes will have the same shape, size and orientation.

Problems based on w = z + k

Example 3.4.4 What is the region of the w plane into which the rectangular region in the Z plane bounded by the lines x = 0, y = 0, x = 1 and y = 2 is mapped under the transformation w = z + (2 – i )

Solution: Given: w = z + (2 - i)

i.e., u + iv = x + iy + (2 − i) = (x + 2) + i (y - 1)

Equating the real and imaginary parts u = x + 2, v = y - 1

Hence, the lines x = 0, y = 0, x = 1 and y = 2 are mapped into the lines u = 2, v=-1, u = 3 and v = 1 respectively which form a rectangle in the w plane.

Example 3.4.5. Find the image of the circle |z|= 1 by the transformation W = z + 2 + 4i

Solution: Given: w = z + 2 + 4i

i.e, u + iv =  x+ iy + 2 + 4i

= (x + 2) + i (y + 4)

Equating the real and imaginary parts, we get

u = x + 2, v = y + 4

⇒x= u - 2, y = v - 4

Given: | z | = 1

i.e., x2+ y2 = 1

 (u − 2)2 + (v - 4)2 = 1

Hence, the circle x2 + y2=1 is mapped into (u - 2)2 + (v - 4)2 = 1 in w plane which is also a circle with centre (2, 4) and radius 1.

2. Magnification

The transformation w = cz, where c is a real constant, represents magnification

i.c., u + iv = c ( x + iy)

u + iv = (cx + i cy)

u = cx, v =cy

.. The image of the point (x, y) is the point (cx, cy).

Hence, the size of any figure in the z-plane is magnified c times, but there will be no change in the shape and orientation. This transformation also transforms circles into circles.

3. Magnification and Rotation

The transformation w = cz, where c is a complex constant, represents both magnification and rotation.

Thus the point (r, θ) in the z-plane is mapped onto the point (ar, θ + α).

This means that the magnitude of the vector representing z is magnified by a = |c| and its direction is rotated through angle α = amp (c). Hence the transformation consists of a magnification and a rotation.

Clearly circles in the z plane are mapped onto circles by this transformation.

Also, every region in the z plane is mapped onto a similar region by this transformation.

Problems based on w = kz

Example 3.4.6. Determine the region 'D' of the w-plane into which the triangular region D enclosed by the lines x = 0, y = 0, x+y=1 is transformed under the transformation w = 2z.

Solution: Let w = u + iv

z = x + iy

Given: w = 2z

u + iv = 2 (x + iy)

u + iv = 2x + i 2y

u = 2x ⇒ x= u/2 v = 2y ⇒ y = v/2

In the z plane the line x=0 is transformed into u = 0 in the w plane

In the z plane the line y=0 is transformed into v=0 in the w plane

 In the z plane the line x+y=1 is transformed into u + v = 2 in the w plane

Example 3.4.7. Find the image of the circle | z | = λ  under the transformation [Anna, May - 2001]

Solution : Given: w = 5z

| w | = 5 | z |

i.e, | w | = 5 λ  [ | z | = λ ]

Hence, the image of | z | = λ in the z plane is transformed into | w |=5λ in the w plane under the transformation w = 5z.

Example 3.4.8. Find the image of the circle | z | = 3 under the transformation w = 2z  [A.U N/D 2012] [A.U N/D 2016 R-13]

Solution :

Given: w  = 2z, | z | = 3

| w | = (2) | z |

= (2)(3) since | z | = 3

= 6

Hence, the image of | z | = 3 in the z plane is transformed into |w = 6 in the w plane under the transformation w = 2z.

Example 3.4.9. Find the image of the region y > 1 under the transformation w = (1-i) z [Anna, May 1999]

Solution :

w = (1 - i) z

u + iv = (1 - i) (x + iy)

= x + iy - ix + y

= ( x + y ) + i (y - x)

i.e, u  = x + y, v = y - x

u + v = 2y  u –v = 2x

y = u + v / 2 x = u – v /2

Hence, image region y > 1 is u + v / 2 > 1, i.e., u + v > 2 in the w-plane

4. Magnification, Rotation and Translation

In general linear transformation w = az + b where a and b are complex constants, represents magnification, rotation and translation.

The transformation w =  az + b can be considered as the combination w of the two simple transformations

w1 = az and w = w1 + b

w1 = az represents magnification by | a | and rotation through amp (a).

w = w1+b represents translation by the vector representing b.

Thus any figure in the z plane will undergo magnification, rotation and translation by the transformation w = az + b.

In particular, circles will be mapped into circles by this transformation.

5. Inversion and Reflection [A.U D15/J16 R-08]

The transformation w = 1/z represents inversion w.r.to the unit circle | z | = 1, followed by reflection in the real axis.

w = 1/z

(or) z = 1/w

x + iy = 1/ u + iv

x + iy = u - iv / u2 + v2

x = u/ u2 + v2......(1)

y = -v / u2 + v2................(2)

We know that, the general equation of circle in z plane is

x2 + y2 + 2gx + 2fy + c = 0 .......(3)

Substitute, (1) and (2) in (3) we get

i.e., c (u2 + v2) + 2gu − 2 fv + 1 = 0..............(4)

which is the equation of the circle in w plane.

Hence, under the transformation w = 1/z a circle in z plane transforms to another circle in the w plane. When the circle passes through the origin we have c =0 in (3). when c = 0, equation (4) gives a straight line.

Problems based on w = 1/z

Example 3.4.10. Find the image of | z- 2i|= 2 under the transformation w = 1/z [Anna - May 1999, May 2001] [A.U N/D 2016 R-8]  [A.U April 2016 R-15 U.D] [A.U A/M 2018 R-17] [A.U A/M 2019 R-17]  [A.U N/D 2019 R-17]

Solution :

Given : |z - 2i| = 2... (1) is a circle.

Centre = 2i i.e, (0,2)

Radius = 2

Given: w = 1/z ⇒z = 1/w

⇒1 + 4v2 + 4v + 4u2 = 4 (u2 + v2)

⇒ 1+ 4y = 0

⇒ v = - ¼

which is a straight line in w-plane.

Example 3.4.11. Find the image of the circle | z-1| = 1 in the complex plane under the mapping w = 1/z  [A.U N/D 2009] [A.U M/J 2016 R-8]

Solution :

Given :  | z - 1| = 1 ... (1) is a circle.san]

Centre = 1,i.e., (1, 0)

Radius = 1

Given: w = ½ ⇒ z = 1/w

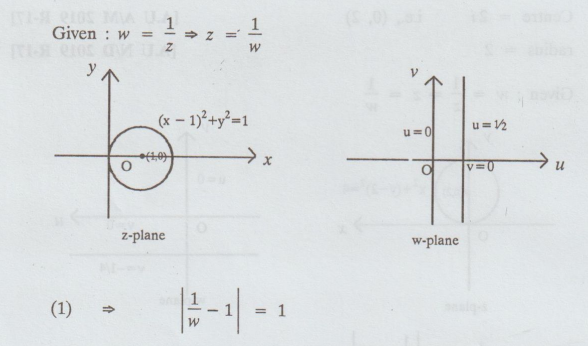
⇒ | 1/w - 1| = 1

⇒ |1 – w | = | w |

 ⇒ | 1- (u + iv) | = | u + iv |

⇒ |1 - u - iv | = | u + iv |

⇒ √(1 − u)² + (-v)² = √ u² + v²

⇒  (1 − u)² + v² = u² + v²

⇒ 1+ u² - 2u + v² = u² + v²

⇒ 2u = 1

⇒ u = 1/2

which is a straight line in the w-plane.

Example 3.4.12. Find the image of the infinite strips  (i)1/4 < y < ½ (ii) 0 < y < ½ under the transformation w = 1/z [A.U Tvli. A/M 2009] [A.U A/M 2017 R8] [A.U A/M 2015 R13, R8]

Solution :

w = 1/z (given)

i.e., z = 1/w

z = 1/u + iv = u – iv/(u + iv) (u - iv) = u – iv / u² + v²

 (i) Given strip is  ¼ < y < 1/2

when  y = 1/4

¼ = iv/u² + v² by (2)

u² + v² = -4v

u² + v² + 4v = 0

u² + (v + 2)² - 4 = 0

u² + (v + 2)² = 4.... (3)

which is a circle se centre is at (0, -2) in the w-plane and radius is 2.

when y = 1/2

½ = -v /u² + v² by (2)

u² + v² = -2v

u² + v² + 2v = 0

u² + (v + 1)² − 1 = 0

u² + (v + 1)² = 1............ (4)

which is a circle whose centre is at (0, -1) in the w-plane and unit radius.

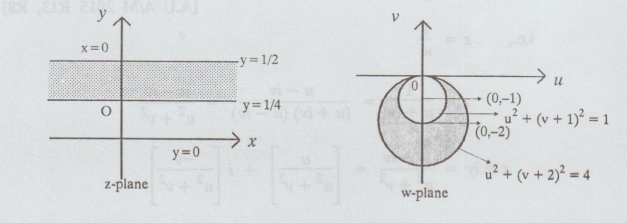
Hence the infinite strip ¼ < y < ½ is transformed into the region in between circles u² + (v + 1)² = 1 and u² + (v + 2)² = 4 in the w-plane.

(ii) Given strip is 0 < y < 1/2

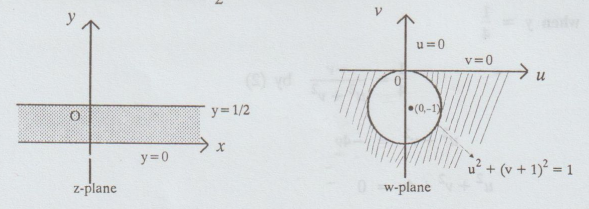
when y = 0

⇒ v = 0 by (2)

when y = ½ we get u² + (v + 1)² = 1 by (4)

Hence, the infinite strip 0 < y < ½ is mapped into the region outside the circle u² + (v + 1)² = 1 in the lower half of the w-plane.

Example 3.4.13. Find the image of x = 2 under the transformation w= 1/z  [Anna May 1998]

Solution: Given: w = 1/z

i.e., z = 1/w

z = 1 / u + iv = u – iv/(u + iv) (u - iv) = u – iv/u² + v²

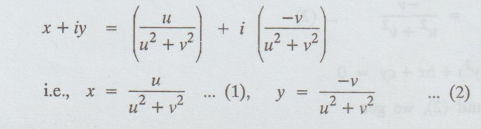
Given: x = 2 in the z-plane

2 = u/u² + v²by (1)

2(u² + v²⁾ = u

u² + v²  - 1/2 u = 0

which is a circle whose centre is ( ¼ , 0)and radius ¼. x = 2 in the z-plane is transformed into a circle

(u – 1/4)² + v² = (1/4)² in the w plane.

Example 3.4.14. What will be the image of a circle containing the origin (i.e., circle passing through the origin) in the XY plane under the transformation w = 1/z ? [Anna - May 2002]

Solution: Given: w = 1/z

i.e., z = 1/w

z = 1/u + iv = u – iv/ (u + iv)(u - iv) = u – iv /u² + v²

u2 i.e., x + iy = [ u/u² + v² ] + i [ -v/u² + v² ]

i.e., x = u/u² + v² ....(1)

y = -v/u² + v² ....(2)

Given: a (x² + y²) + bx + cy = 0

Substitute, (1) and (2), we get

a + bu – cv = 0

Therefore the image of circle passing through the origin in the XY-plane is a straight line in the w-plane.

Example 3.4.15. Determine the image of 1 < x < 2 under the mapping w = 1/z [Anna May 2001, April 2017 R-15 U.D]

Solution: Given: w = 1/z

i.e., z = 1/w

z = 1/ u + iv = u – iv/(u + iv) (u – iv) = u – iv / u² + v²

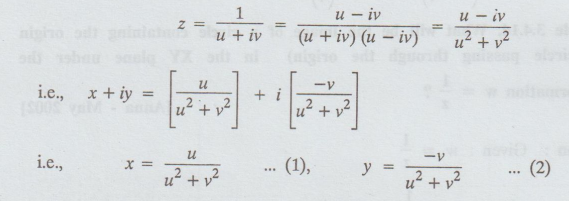
Given : 1 < x < 2

When x = 1

1 = u /u² + v² by (1)

u² + v² = u

u² + v² – u = 0

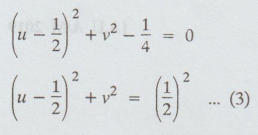
which is a circle whose centre is (1/2 , 0)and radius 1/2

when x = 2

2 = u /u² + v² by (1)

2 (u² + v²) = u

 u² + v² – u/2 = 0

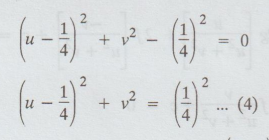
which is a circle whose centre is (1/4 , 0) and radius is 1/4

Hence, the infinite strip 1 < x < 2 is transformed into the region in between the circles (3) and (4) in the w plane.

Example 3.4.16. Show that the transformation w = 1/z transforms all circles and straight lines in the z-plane into circles or straight lines in the w-plane. [A.U. N/D 2007, J/J 2008, N/D 2011] [A.U N/D 2016 R-13] [A.U A/M 2017 R-13] [A.U A/M 2019 R-08]

Solution: Given: w = 1/z

i.e., z = 1/w

Now, w = u + iv

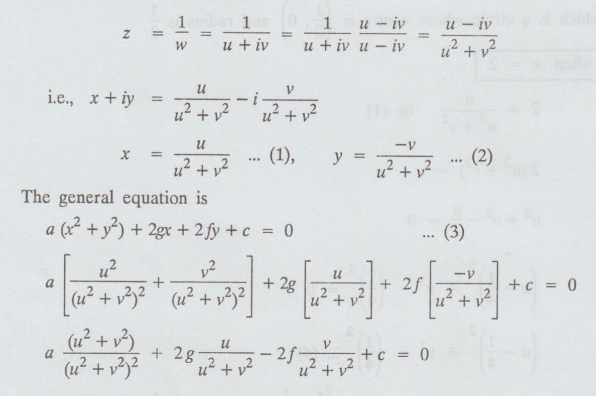
The transformed equation is

c (u² + v²) + 2gu - 2fv + a = 0 ....(4)

 (i) a ≠ 0, c ≠ 0⇒ circles not passing through the origin in z-plane map into circles not passing through the origin in the w-plane.

(ii) a ≠ 0, c = 0 ⇒ circles through the origin in z-plane map onto straight lines not through the origin in the w-plane.

(iii) a = 0, c ≠ 0 ⇒the straight lines not through the origin in z-plane map onto circles through the origin in the w-plane.

(iv) a = 0, c = 0 ⇒ straight lines through the origin of z-plane onto straight lines through the origin in the w-plane.

Example 3.4.17. and the image of the hyperbola x - y = 1 under the transformation w =1/z. [A.U M/J 2010, M/J 2012][A.U N/D 2012]

Solution: Given: w = 1/z ⇒ z = 1/w

x + iy = 1/Re^iϕ

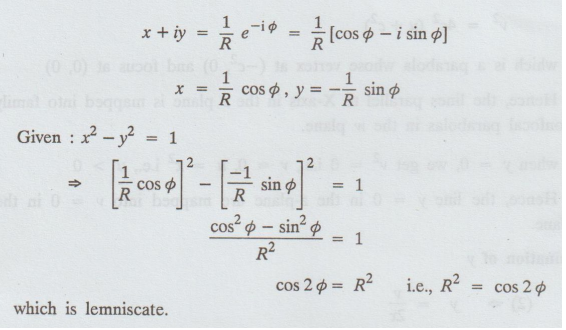
cos 2ϕ = R² i.e., R² = cos 2ϕ

which is lemniscate.

Problems based on w = Z²

Example 3.4.18. Discuss the transformation w = z² [Anna - May 2001]

Solution : w = z²

u + iv = (x + iy)² = x² + (iy)² + i 2xy = x² - y² + i 2xy

i.e. u = x² – y²,... (1), v = 2xy ......(2)

Elimination of x:

(2) ⇒ x = v/ 2y

 (1) ⇒ u = (v/2y)² – y²

u = v²/4y² – y²

4uy² = v² – 4y⁴

4uy² + 4y⁴ = v²

y² [4u + 4y²] = v²

4y² [u + y²] = v²

v² = 4y² (v² + u)

when y = c ( ≠ 0), we get

v² = 4c² (u + c²)

 which is a parabola whose vertex at (-c², 0) and focus at (0, 0)

Hence, the lines parallel to X-axis in the z plane is mapped into family of confocal parabolas in the w plane.

when y = 0, we get v² = 0 i.e., v = 0, u = x² i.e., u > 0

Hence, the line y = 0 in the z-plane are mapped into v = 0 in the w plane.

Elimination of y

 (2) ⇒ y = v/2x

 (1) ⇒ u = x² – (v/2x)²

u =x² – v²/4x²

v²/4x² = x² - u

v² = (4x²) (x² - u)

when x = c (#0), we get v2 = 4c²(c² – u) = -4c²(u – c²)

which is a parabola whose vertex at (c², 0) and focus at (0, 0) and axis lies along the u- axis and which is open to the left.

Hence, the lines parallel to y axis in the z plane are mapped into confocal parabolas in the w plane when x = 0, we get v² = 0. i.e., v = 0, u = -y² i.e., u < 0

i.e., the map of the entire y axis is the negative part or the left half of the u axis.

Example 3.4.19. Fad the image of the hyperbola x² – y² = 10 under the transformation w = z² if w = u + iv [Anna May 1997]

Solution : w = z²

u + iv = (x + iy)²

 = x² + (iy)² + i 2xy

i.e. u = x² – y²,... (1)

 v = 2xy ......(2)

given : x² - y² = 10

i.e., u = 10

Hence, the image of the hyperbola x² - y² = 10 in the z plane is mapped into u = 10 in the w plane which is a straight line.

Example 3.4.20. Determine the region of the w plane into which the circl | z-1|= 1 is mapped by the transformation w = Z². [Anna, May 2001]

Solution: In polar form z = re^iθ, w = Re^iϕ

Given: |z - 1| = 1

i.e., | re^iθ -1 | = 1

 (1) r² = (2 cosθ)²

r² = 4 cos² θ

= 4 [1+ cos 2θ /2]

r² = 2 [ 1+ cos 2θ ]

R = 2 [ 1 + cos ϕ ] by (2)

which is a Cardioid.

Example 3.4.21. Find the image under the mapping w = Z² of the triangular region bounded by y = 1, x = 1 and x + y = 1 and plot the same. [Anna, Oct., 1997] [A.U A/M 2019 R-13]

Solution: In Z-plane given lines are x = 1, y = 1, x + y = 1

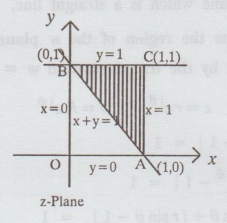
Given: w = z²

u + iv = (x + y)²

u + iv = x² – y² + 2xy i

Equating the real and imaginary parts, we get

u = x² - y² ...(1)

v = 2xy .....(2)

when x + y = 1

 (1) ⇒ u = (x + y) (x − y)

u = x – y [ x + y = 1]

Example 3.4.22. Prove that the transformation w = z/1 – z maps the upper half of the z plane into the upper half of the w plane. What is the image of the circle |z| = 1 under this transformation. [Anna, May 2001]

Solution :

Given: | z | = 1 is a circle.

Centre = 0 i.e., (0, 0)

Radius = 1

Given: w = z/1- z

z = w/ w + 1

| z | = | w /w + 1| = | w |/|w + 1|

Given | z | = 1

| w |/|w + 1| = 1

| w | = | w + 1 |

| u + iv | = | u + iv + 1 |

u² + v² = (u + 1)² + v²

u² + v² = u² + 2u + 1 + v²

0 = 2u + 1

u = -1/2

Further the region | z | < 1 transforms into u > -1/2

Problems based on on critical points of the transformation

Example 3.4.23. Find the critical points of the transformation w2 = (z - α) (z - β). [A.U Oct., 1997] [A.U N/D 2014] [A.U M/J 2016 R-13]

Solution: Given: w² = (z - α) (z - β)...(1)

Critical points occur at dw/dz = 0 and dz/dw = 0

differentiation of (1) w.r.to z, we get

⇒ w = 0

 (z - α) (z - β) = 0

 z = α, β

The critical points are α + β /2 , α and β.

Example 3.4.24. Find the critical points of the transformation w = z² + 1/z² IAU A/M [A.U A/M 2017 R-13]

Solution: Given: w = z² + 1/z² ....(1)

Critical points occur at dw/dz = 0 and dz/dw = 0

differentiation of (1) w.r.to z, we get

dw/dz = 2z – 2/z³ = 2z⁴ – 2 /z³

The critical points are ±1, ±i, 0

Example 3.4.25. Find the critical points of the transformation w = z + 1/z

Solution: Given: w = z + 1/z

Critical points occur at dw/dz = 0 and dz/dw = 0

differentiation of (1) w.r.to z, we get

dw/dz = 1 – 1/z² = z² – 1/z²

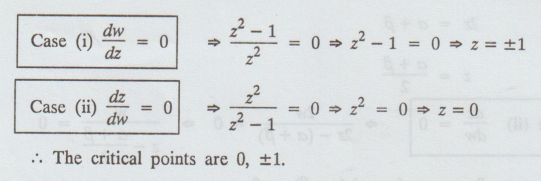
The critical points is z = 0, ±1.

Example 3.4.26. Find the critical points of the transformation w = 1 + 2/z [A.U N/D 2013 R

Solution: Given: w = 1 + 2/z

Critical points occur at dw/dz = 0 anddz/dw = 0

differentiation of (1) w.r.to z, we get

dw/dz = -2/z²

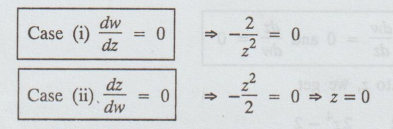
The critical point is z = 0