Spherical Co-ordinate System

Spherical Co-ordinate System

AU : May-05, 10,18, Dec.-07, 08.18

• The surfaces which are used to define the spherical co-ordinate system on the three cartesian axes are,

1. Sphere of radius r, origin as the centre of the sphere.

2. A right circular cone with its apex at the origin and its axis as z axis. Its half angle is θ. It rotates about z axis and θ varies from 0 to 180s.

3.A half plane perpendicular to xy plane containing z axis, making an angle ϕ with the xz plane.

• Thus the three co-ordinates of a point P in the spherical co-ordinate system are (r, θ,ϕ). These surfaces are shown in the Fig. 1.8.1.

• The ranges of the variables are,

0 ≤ r < ∞... (1.8.1)

0 ≤ ϕ ≤ 2π ... (1.8.2)

0 ≤ θ ≤ π ... (1.8.3)

• The point P (r, θ,ϕ) can be represented in the spherical co-ordinate system as shown in the Fig. 1.8.2. The angles θ and ϕ are measured in radians.

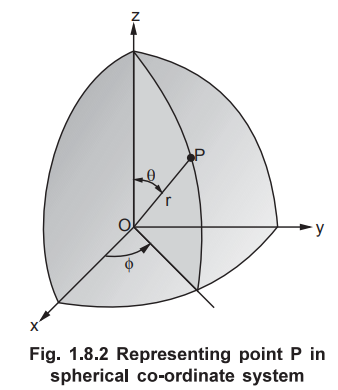
• The point P can be defined as the intersection of three surfaces in spherical co-ordinate system. These three surfaces are,

r = Constant which is a sphere with centre as origin.

θ = Constant which is right circular cone with apex as origin and axis as z-axis.

Φ = Constant is a plane perpendicular to xy plane.

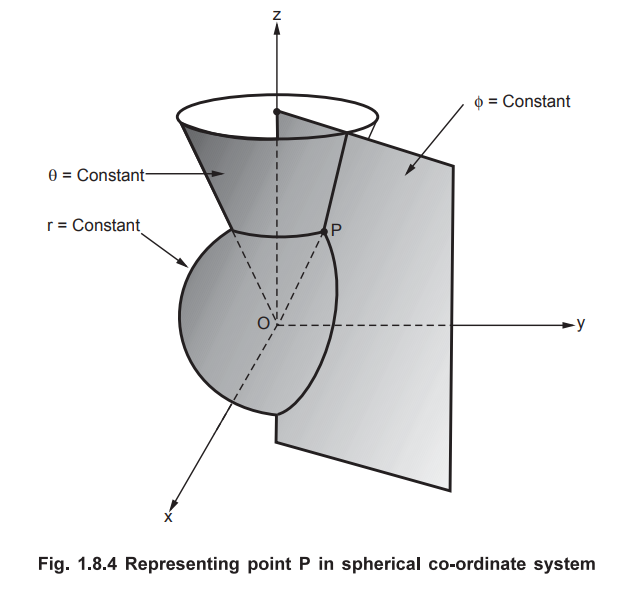
• The surfaces are already shown in the Fig. 1.8.1. The intersection of the sphere i.e. r = Constant surface and right circular cone i.e. θ = Constant surface is a horizontal circle as shown in the Fig. 1.8.3. As seen from the Fig. 1.8.3, the radius of this circle is r sin θ.

• Now consider intersection of ϕ = Constant plane with the intersection of r = Constant and θ = Constant planes as shown in the Fig. 1.8.4. This defines a point P.

1. Base Vectors

• Similar to other two co-ordinate systems, there are three unit vectors in the r, θ and ϕ directions denoted as 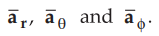 These unit vectors are mutually perpendicular to each other and are shown in the Fig. 1.8.5. The unit vector  is directed from the centre of the sphere i.e. origin to the given point P. It is directed radially outward, normal to the sphere. It lies in the cone θ = Constant and plane ϕ = Constant.

 

• The unit vector a  is tangent to the sphere and oriented in the direction of increasing θ. It is normal to the conical surface.

• The third unit vector  is tangent to the sphere and also tangent to the conical surface. It is oriented in the direction of increasing ϕ. It is same as defined in the cylindrical co-ordinate system.

• Hence vector of point P can be represented as,

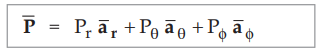 ......(1.8.4)

• where P_r is the radius r and I P_θ, P_ϕ are the two angle components of point P.

 

2. Differential Elements in Spherical Co-ordinate System

• Consider a point P (r,θ,ϕ,) in a spherical co-ordinate system. Let each co-ordinate is increased by the differential amount. The differential increments in r, θ, ϕ are dr, dθ and dϕ.

• Now there are two spheres of radius r and r + dr. There are two cones with half angles θ and θ + dθ. There are two planes at the angles ϕ and ϕ + dϕ measured from xz plane. All these surfaces enclose a small volume as shown in the Fig. 1.8.6.

 

• The differential length in r direction is dr. The differential length in 0 direction is r sin θ dϕ. The differential length in θ direction is r d θ. Thus,

dr = Differential length in r direction ...       (1.8.5)

rd θ = Differential length in θ direction       ...       (1.8.6)

r sin θ dϕ = Differential  length          in ϕ direction       ...       (1.8.7)

θϕ• Hence the differential vector length in spherical co-ordinate system is given by,

....(1.8.8)

• the magnitude of the differential length vector is given by,

 ....(1.8.9)

 • Hence the differential volume of the differential element formed, in spherical co-ordinate system is given by,

dv = r² sin θ dr dθ dϕ......(1.8.10)

• The differential surface areas in the three directions are shown in the Fig. 1.8.7.

 • The vector representation of these differential surface areas are given by,

 = Differential vector surface area normal to r direction = r² sin θ dθ dϕ......        ...(1.8.11)

 = Differential vector surface area normal to θ direction = r sin θ dr dϕ      ...(1.8.12)

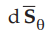 = Differential vector surface area normal to ϕ direction = r dr dθ     ... (1.8.13)

 

3. Relationship between Cartesian and Spherical Systems

• Consider a point P whose cartesian co-ordinates are x, y and z while the spherical co-ordinates are r, θ and r² and ϕ as shown in the Fig. 1.8.8.

• Looking at the xy plane we can write,

x = rsin θ cos ϕ and

y = rsin θsin ϕ

While z = rcos θ

• Hence the transformation from spherical to cartesian can be obtained from the equations,

x = r sin θ cos ϕ, y = r sin θ sin         ϕ and z = r cos θ

• Now r can be expressed as,

x² + y² + z² = r²sin²θcos² ϕ+ r² sin² θsin²ϕ + r² cos² θ

= r² sin² θ[sin² ϕ + cos² ϕ] + r² cos² θ

= r² [sin² θ + cos² θ]=r²

r = √x² + y² + z² 

While tan ϕ = y/x and cos θ = z/r

• As r is known, θ can be obtained.

• Thus the transformation from cartesian to spherical co-ordinate system can be obtained from the equations,

 .... (1.8.15)

• Remember that r is positive and varies from 0 to ∞ varies from 0 to π radians i.e. 0^o to 180° and ϕ varies from 0 to 2 π radians i.e. 0° to 360°.

Key Point : While using above formulae, care must be taken to place the angles 0 and 6 in the correct quadrants according to the signs of x, y and z.

 

Ex. 1.8.1 Calculate the volume of a sphere of radius R using integration.

Sol. : The differential volume of a sphere is,

 dv = r² sin θ dr d√θ dϕ

The limits for r are 0 to R, as sphere is of radius R.

The θ varies from 0 to π while 6 varies from 0 to 2 π.

 

Ex. 1.8.2 Use spherical co-ordinates and integrate to find the area of the region 0<ϕ<α on the spherical shell of radius α. What is the area if α = 2π ?

Sol. : Consider the spherical shell of radius a hence r = a is constant.

Consider differential surface area normal to r direction which is radially outward.

dS_r = r² sin θ d θ dϕ = a²sin θ dθ dϕ  ... as r = a

But ϕ is varying between 0 to a while for spherical shell 0 varies from 0 to π.

So area of the region is 2 a₂ α.

If α = 2π the area of the region becomes 4πa², as the shell becomes complete sphere of radius a when ϕ varies from 0 to 2π .

 

Ex. 1.8.3 Given the two points A (x = 2, y = 3, z = -1)   (r = 4, θ = 25, ϕ = 120^o) Find the spherical co-ordinates of A and cartesian co-ordinates of B. AU: May-10 Marks 8

Sol. : i) A (x =2, y =3, z = -l)

To convert to spherical co-ordinates.

r = √x² + y² + z²

= √(2)² + (3)² + (-1)² = √14 = 3.7416

θ = cos^-1[z/√x² + y² + z²

= cos^-1[-1/√-14] = 105.5^o

ϕ = tan^-1 y/x = tan^-1 3/2 = 56.31^o

A (3.7416, 105.5°, 56.31°) in spherical system.

ii) B (r = 4, 0 = 25^o, ϕ = 120^o) hence to convert to cartesian co-ordinates,

x = r sin θ cos ϕ = 4 × sin 25° × cos 120° = - 0.845

y = r sin θ sin ϕ = 4 × sin 25° × sin 120° = 1.464

 z = r cos θ = 4 × cos 25° = 3.625

B (- 0.845, 1.464, 3.625) in cartesian system.

Examples for Practice

Ex. 1.8.4 Convert point P(l, 3, 5) from cartesian to cylindrical and spherical co-ordinates. [Ans.: P (3.1622, 71.56°, 5), P( 5.916, 32.31^o,71.56^o)]

Ex. 1.8.5 Convert the point P(3, 4, 5) from cartesian to spherical co-ordinates. [Ans.: P(7.071, 45°, 53.13^o)]

Review Question

1.Discuss the spherical co-ordinate system used to represent field vectors. AU : May-05,18, Dec.-08, Marks 5