Stability of an Op-amp

Stability of an Op-amp

As mentioned earlier, op-amps are rarely used in the open loop configuration. Due to its use in closed loop configuration, it is necessary to study the effect of feedback on the circuit stability.

Consider the noninverting amplifier with resistive feedback as shown in the Fig. 2.31.1.

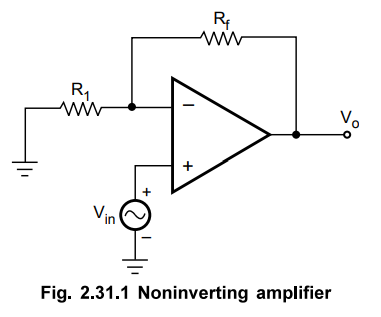
The open loop gain of the op-amp is frequency dependent and can be denoted as AOL(f). To determine the stability of such circuit, it is necessary to represent the circuits in the standard form of a block diagram, as shown in the Fig. 2.31.2

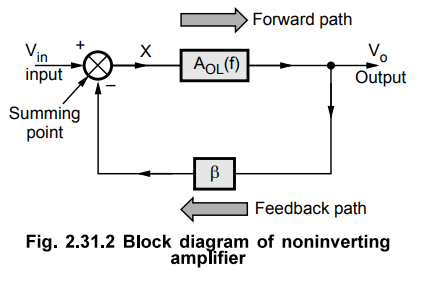
The block between output and input is called forward block while the block between output signal and the feedback is called feedback block. The transfer function or gain of forward block is A_OL(f) while the transfer function or gain of feedback block is β. Let us investigate the stability of such a system with the help of frequency response approach.

Key Point The feedback block uses only resistive elements and hence its transfer function P is independent of frequency and is constant.

From the Fig. 2.31.2 we can write,

The ratio V_o/V_in with feedback is called closed loop gain of the amplifier while the product A_OL(f) β is called loop gain which is generally used to determine the stability.

The stability of the circuit entirely depends on the behaviour of the roots of the characteristic equation of the system, which is

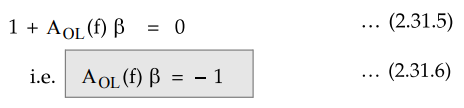
This can be expressed in the complex form as

A_OL(f) β = - 1 + j0

From this, the conditions for the sustained oscillations can be obtained. Equating angles and magnitudes of both sides of the equation (2.31.7) we get,

The equation (2.31.8) is the magnitude condition while the equation (2.31.9) is the angle condition. At a particular frequency, both the conditions may get satisfied and there is every possibility that the amplifier may begin to oscillate. These conditions are called Barkhausen Criterion for the sustained oscillations.

Now oscillations is the verge of instability. The system is said to be stable if its output reaches a fixed value within a finite time. While if output increases with time indefinitely or there is output without input, the system is said to be unstable.

Key Point So determining stability of the circuit means actually deciding how close the circuit is to the conditions of sustained oscillations which indicates the starting point of instability.

This is possible from the frequency response of the circuit by defining certain specifications.

1. Stability Specifications from Frequency Response

The loop gain A_OL(f) β is used to obtain the frequency response of the system over a desired range of frequency, as mentioned earlier. Once the magnitude plot and phase angle plot (Bode plot) is obtained, the following specifications are determined, from which system stability can be decided.

i) Gain Cross Over Frequency (ω_gc) :

The frequency at which the loop gain magnitude (|A_OL(f) β) is unity ie- 20 log | A_OL(f) β | = 0 dB is called gain cross over frequency and denoted as ω_gc.

ii) Phase Cross Over Frequency (ω_pc) :

The frequency at which the phase shift introduced by the loop gain is -180° or nπ radians is called phase cross over frequency and denoted as ω_pc.

iii) Gain Margin (G.M.) :

The critical values of loop gain are 0 dB and -180° from the stability point of view. How far away the circuit is from this point of instability can be decided by determining loop gain at phase cross over frequency. This gain measured at the frequency ω = ω_pc is called gain margin. So loop gain | A_OL(f) β | measured at to = ω = ω_pc is the gain margin of the circuit. Mathematically it can be expressed as

G.M = - 20 log |A_OL(f) β | ω = ω_pc dB  …. (2.31.10)

iv) Phase Margin (P.M.) :

Similar to the gain at phase cross over frequency, one more specification can be defined from the phase shift of loop gain existing at gain cross over frequency. This specification is called phase margin.

The amount by which angle of the loop gain (∠A_OL(f) β | ω = ω_gc) differ from the -180^o phase shift, at ω = ω_gc is called phase margin. Mathematically it is expressed as

P.M = 180^o + ∠A_OL(f) β | ω = ω_gc  …. (2.31.11)

2. Stability Criterion

When ω = ω_gc  = ω_pc, both angle and magnitude conditions as per Barkhausen criterion get satisfied and circuit oscillates. The system in such a case is called marginally stable.

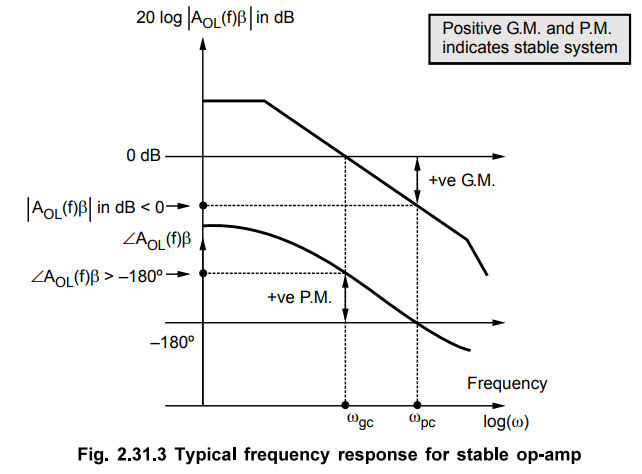
If G.M. is positive i.e. gain | A_OL(f) β | in dB is negative at ω = ω_pc  , the system is said to be stable. Similarly if P.M. is positive i.e. | A_OL(f) β | is greater than -180°, the system is said to be stable.

The negative values of G.M. and P.M., indicate instability of the system.

Key Point More positive are the values of G.M. and P.M., more stable is the system.

The Fig. 2.31.3 shows the positive G.M. and P.M. for the stable system on the frequency response.

Review Questions

1. Write a note on stability criteria for op-amp.

2. What is the stability of an op-amp ? Explain the various stability specifications.