Stability of Nucleus: Mass defect, Binding energy

Unit – V

Chapter 7

Energy Sources

 

INTROUDUCTION

For our energy requirement, we mainly depond on the conventional sources of energy like coal, petroleum, natural gas, etc., These sources are limited in quantity and can be exhausted in near future. This is because of their continuous and rapid use.

To overcome this energy crises the scientists have accelerated the search and use of non- conventional (renewable) sources of energy, solar energy, nuclear energy, etc,

 

 STABILITY OF NUCLEUS

1. Mass defect

It has been found that the actual mass of an isotope is always less than the sum of the masses of the protons, neutrons and electron from which it is formed.

Definition

The difference between the calculated and experimental masses of nucleus is called mass defect. It is denoted by ∆m.

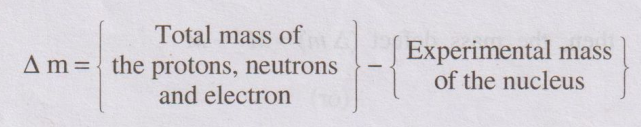
 (or)

It is defined as the loss of mass during the formation of the nucleus of the isotope.

Calculation of mass defect

Consider an isotope,

let its atomic number = Z

Mass number = A

If its atom contains

Z protons, Z electrons and (A-Z) neutrons

Let,

m_p = mass of proton

m_n = mass of neutron

m_e = mass of an electron

ஃ Calculated mass of isotope

M' = Z m_p + Zm_e + (A - Z)m_n

= Z_mH + (A - Z) m_n

(where, m_p + m_e = mass of H atom = m_H)

Let,

M = Actual experimental mass of the nucleus,

then, the mass defect (A m) = M'-M

(or)

∆m= Z_mH + (A - Z) m_n-M

 

Problems on Mass defect

1. Calculate the mass defect of ₂₀Ca⁴⁰ , which has atomic mass of 39.975 amu. The mass of proton is 1.0078 amu and the mass of neutron is 1.0086 amu.

Solution

Mass defect (∆m) of Ca-atom = Zm_p + (A - Z) m_n - M

Note

Calcium atom is composed of 20 protons and 20 neutrons.

Given: Z = 20; (A - Z) = 20; m_H = 1.0078 amu ;

m_n = 1.0086 amu; M = 39.975 amu;

ஃ ∆m = [ 20 m_p + 20 m_n -M] [m_e = Neglected]

= [20 × 1.0078 + 20 × 1.0086 – 39.975]

= [20.156 + 20.172 – 39.975]

= 40.328 – 39.975

= 0.353 amu

 

2. Calculate the mass defect of ₂He⁴, if its experimentally determined mass is 4.00390 amu. The masses of a proton, an electron and a neutron are 1.007825, 0.0005852 and1.008668 amu respectively.

Solution

Mass defect (Am) of He-atom = [2m, + 2me + 2mn-M]

Note

₂He⁴ atom is composed of 2 protons, 2 electrons and 2 neutrons.

Given: m_p = 1.007825 amu; m_e = 0.0005852 amu ;

m_n = 1.008668 amu

ஃ ∆m= [2 × 1.007825 + 2 × 0.0005852 + 2 × 1.008688 - 4.00390] amu

= [4.0341964 – 4.00390] amu

= 0.0302964 amu

 

3. Mass of hydrogen and neutron are 1.008 amu and 1.0072 amu respectively. If experimentally determined mass of sodium atom (₁₁Na²³) is 23.0092 amu. Calculate mass defect.

Solution

Mass defect of Na-atom

(∆m) = [ 11 × m_H + 12m_n – M ]

Note

₁₁Na²³ is made up of 11-H-atom and 12-neutrons.

Given: m_p (or) m_H = 1.008 amu; m_n = 1.0072 amu ;

M= 23.0092

ஃ ∆_m = [ 11 × 1.008 + 12 × 1.0072 – 23.0092 ] amu

= 0.1652 amu

 

4. Calculate the mass defect of -particles. Given that the mass of proton = 1.00758 amu, mass of neutron = 1.00897 amu and mass of helium nucleus = 4.00820 amu.

Solution

Mass defect (∆m) of ɑ -particle = [2m_p + 2m_n - M]

Note

An ɑ - particle is composed of 2 protons and 2 neutrons

Given: m_p = 1.00758 amu; m_n= 1.00897 amu ;

M = 4.00820 amu

ஃ∆m = [ 2 × 1.00758 + 2 × 1.00897 – 4.00820 ) amu

= 0.02490 amu

 

5. Calculate the mass defect of the following fission reaction.

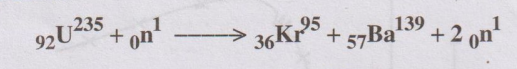
Given that atomic mass of U²³⁵ = 235.124 amu;

Kr⁹⁵ = 94.945 amu ; Ba¹³⁹ = 138.954 amu; ₀n¹ = 1.0099 amu

Solution

ஃ ∆m= Atomic mass of [U+n - (Kr + Ba + 2n)]

= [235.124 + 1.0099 – (94.945 + 138.954 + 2 × 1.0099)]

= 236.1339 – (233.899 + 2.0198)

= 236.1339 - 235.9188

= 0.2151 amu

 

2. Binding energy

Loss of mass during the formation of nucleus from nucleons gets converted into energy. This energy is known as binding energy. Binding energy is responsible for the stability of the nucleus. The greater the energy liberated the greater is the stability of the nucleus. Hence, binding energy (BE) is the energy equivalent of mass defect.

Definition

Binding energy is defined as the energy released when a given number of protons and neutrons coalesee to form nucleus.

(or)

It is the energy required to disrupt the nucleus into its constituent protons and neutrons.

Binding Energy Vs Nuclear Stability

A plot of Binding energy per nucleon against mass number for different elements gives the following graph:

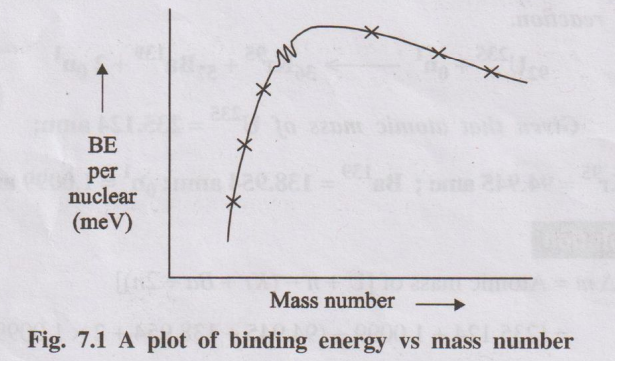
Fig. 7.1 A plot of binding energy vs mass number

The graph shows that BE and hence the stability of nucleus increases upto a mass number of 65 and decreases thereafter. There are some subsidiary peaks in the plot at ₂He⁴, ₆C¹² and ₈O¹⁶ indicating stable nuclear configurations. This is probably due to the presence of equal number of protons and neutrons.

Calculation of binding energy

Binding energy can be calculated from the mass defect using the relation.

E = ∆ m c²

E = [Zm_H + (A - Z) m_n - M] × c²

where, E - Binding energy of the nucleus

∆ m - Mass defect

c - Velocity of light (3 × 10⁸ m/s)