Stoke's Theorem

Stoke's Theorem

AU: May-09,10, Dec.-10,11,12,13

• The Stoke's theorem relates the line integral to a surface integral. It states that,

• The line integral of  around a closed path L is equal to the integral of curl of  over the open surface S enclosed by the closed path L.

• Mathematically it is expressed as,

where dL = Perimeter of total surface S

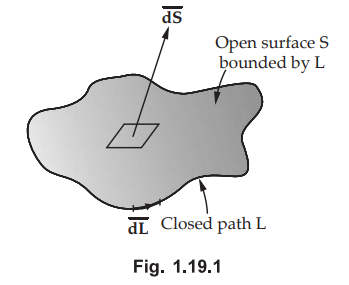
Key Point : Stoke's theorem is applicable only when  are continuous on the surface S. The path L and open surface S enclosed by path L for which Stoke's theorem is applicable are shown in the Fig. 1.19.1.

1. Proof of Stoke’s Theorem

• Consider a surface S which is splitted into number of incremental surfaces. Each incremental surface is having area AS as shown in the Fig. 1.19.2 (a).

• Applying definition of the curl to any of these incremental surfaces we can write,

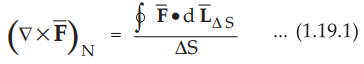
dLAS = Perimeter of the incremental surface AS

• Now the curl of  in the normal direction is the dot product of curl of  with  where  is unit vector, normal to the surface ΔS, according to right hand rule.

p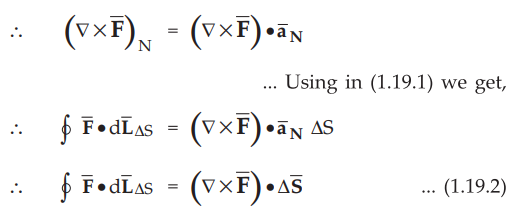

• To obtain total curl for every incremental surface, add the closed line integrals for each ΔS. From the Fig. 1.19.2 (b), it can be seen that at a common boundary between the two incremental surfaces, the line integral is getting cancelled as the boundary is getting traced in two opposite directions.

• This happens for all the interior boundaries. Only at the outside boundary cancellation does not exist. Hence summation of all closed line integrals for each and every ΔS ends up in a single closed line integral to be obtained for the outer boundary of the total surface S. Hence the equation (1.19.2) becomes,

where          dL = Perimeter of the total surface S

• Thus line integral can be expressed as a surface integral which proves the Stake's theorem.

Key Point : The Stake's theorem is applicable for the open surface enclosed by the given closed path. Any volume is a closed surface and hence application of Stake's theorem to a closed surface which encloses certain volume, produces zero answer.

Ex. 1.19.1 Given that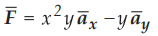  

i) Find 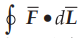where L is shown in Fig. 1.19.3. 

ii) verify Stoke’s theorem. AU: may-09, Marks 8

Sol. : i) The path of L is shown in the Fig. 1.19.3(a)

Now split the area inS^o triangles. For the first triangle the equation of line is y = x hence use dy = x. And x varies from 1 to 0. For the second triangle, the equation of line is y = - x + 2 hence used dy = - x + 2 and x varies from 2 to 1.

Thus Stake's theorem is verified

Ex. 1.19.2 If 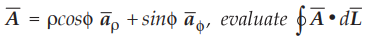 around the path shown in Fig. 1.19.4. Confirm this using Stoke’s theorem. AU : May-10, Marks 8

Sol. :

Ex. 1.19.3 

Ex. 1.19.4 Given that 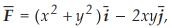 evaluate both sides of Stoke's theorem for a rectangular path bounded by the lines x = ± a, y = 0, y = b. AU : Dec.-12, Marks 10

Sol. : The path L is shown in the Fig. 1.19.6.

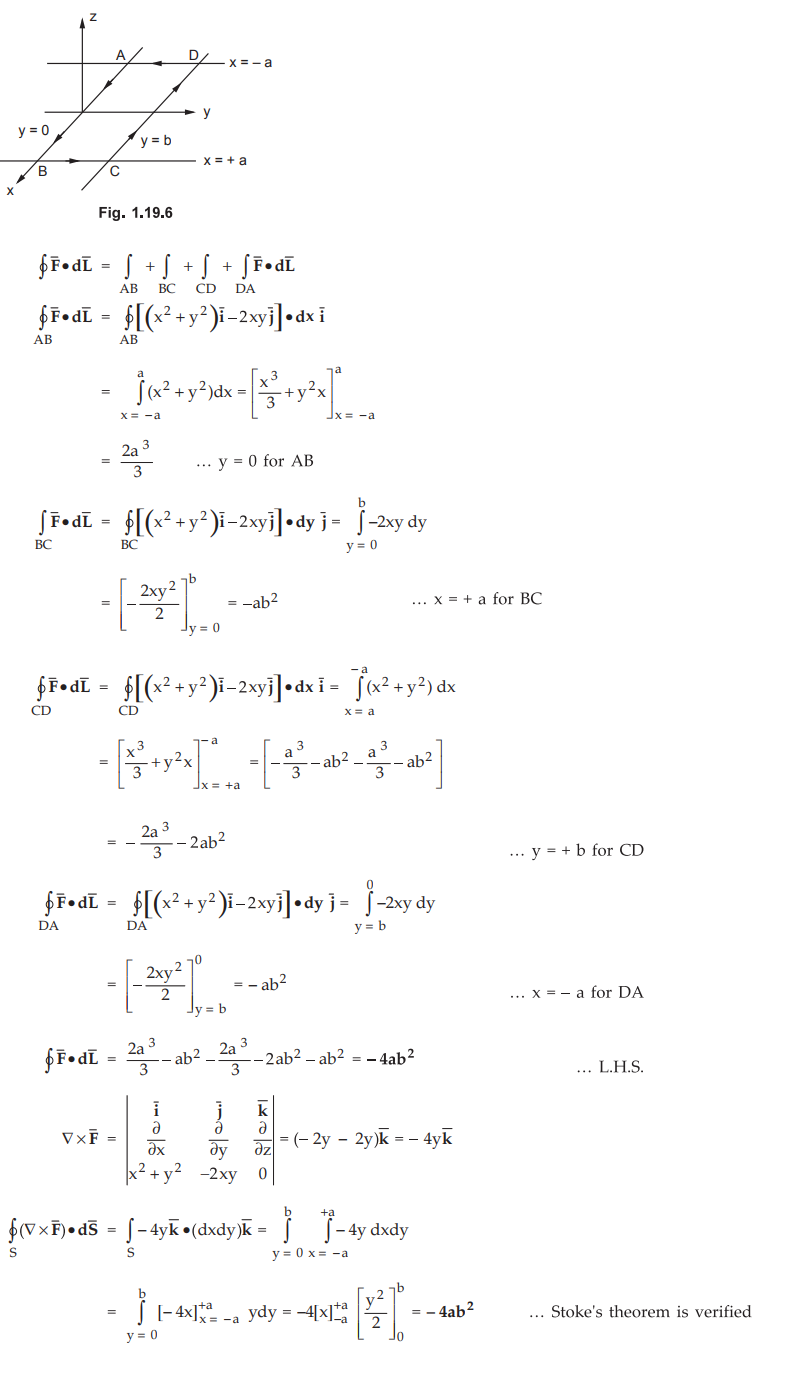
Examples for Practice

Ex.e 1.19.5 Evaluate both sides of the Stoke's theorem for the field  A/m an^ the rectangular path around the region, 2 ≤ x ≤ 5, -1 ≤ y ≤ 1, z = 0. Let the positive direction of 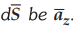 [Ans.: -126 A]

Ex. 1.19.6 Evaluate both sides of Stoke's theorem for the field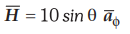 and the surface r = 3, 0 ≤ 0 ≤ 90^o 0 ≤  b ≤  90^o Let the surface have the  direction.  [Ans.: 47.1238 A]   

Review Question

1.Write a note on stoke’s theorem. AU: Dec.-10, 13, Marks 4