String Efficiency

String Efficiency

AU : Oct.-01, April-98, 99, 05, May-04, 07, 11, 12,15,18, Dec.-05, 08, 11, 13,16

The nonuniformity in the voltage distribution over a string of suspension insulators is expressed in terms of a parameter called "string efficiency".

The string efficiency is defined as the ratio of total voltage across the string to the product of number of units and the voltage across the unit adjacent to the line conductor.

Mathematically it can be expressed as,

where            n = Number of units or discs in the string

The string efficiency is calculated based on the string used for each line and hence the voltage across the string is the voltage of conductor with respect to earth i.e. phase voltage.

More the value of the string efficiency, more uniform is the voltage distribution across the string. For the ideal case, the string efficiency is 100 % and the voltage across each disc of the string is equal. Practically various methods are used to obtain the string efficiency as high as possible.

In the rainy season, insulators are wet and the mutual capacitance value increases. Thus the ratio of shunt to mutual capacitance i.e. k decreases. This increases the uniformity of the voltage distribution. Hence in rainy season, string efficiency is higher.

 

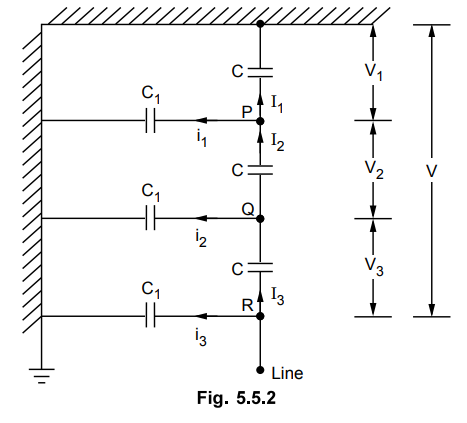
1. Method of Calculating String Efficiency

Consider a string of suspension insulator consisting of 4 discs. The voltage distribution will be as shown in the Fig. 5.5.1.

Let C₁ = kC

Thus the shunt capacitance is k times the mutual capacitance.

Applying Kirchhoff's current law at node P,

I₂ = i₁ + I₁    ... (5.5.1)

The current through capacitor is the ratio of voltage across capacitor and the capacitive reactance of the capacitor. 

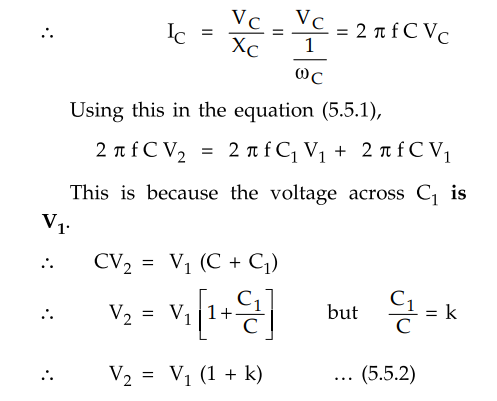
Similarly applying Kirchhoff's current law at node Q,

I₃ = i₂ + I₂    ... (5.5.3)

Note that the voltage across the shunt capacitance C₁ carrying current i₂ is V₁ + V₂.

Note that the voltage across the shunt capacitance C₁ carrying current i₃ is (V₁ + V₂ + V₃)

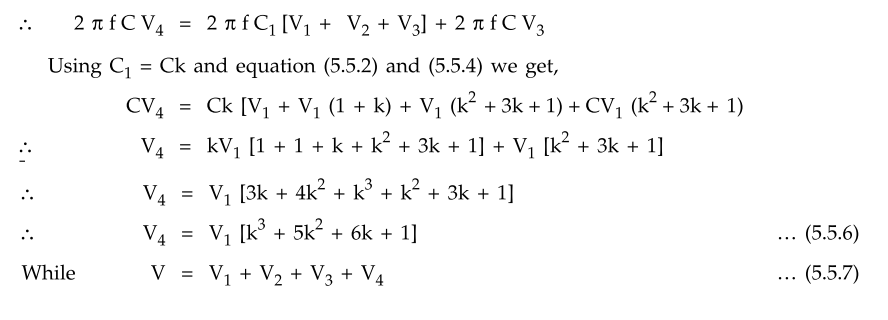
Hence using equations (5.5.2), (5.5.4), (5.5.6) and (5.5.7) all the voltages for given value of k can be calculated.

Thus it can be seen that the voltage across the unit nearest to the line conductor is maximum.

Now String efficiency = V / n × V₄ = 6.8906 V₁/ 4 × 2.8281 V₁ for n 4 60.91 %

Thus for n = 4 and k = 0.25, the string efficiency is just 60.91 %. More the value of k, greater is the nonuniformity and lesser is the string efficiency. While as the number of units in a string increases, the string efficiency decreases and its calculation becomes much more tedious. Hence the string with less number of units is more effective.

 

Example 5.5.1 Each line of a three phase system is suspended by a string of three similar insulators. If the voltage across the line unit is 20 kV, calculate the line to neutral voltage and the string efficiency. Assume that the shunt capacitance between each insulator and earthed metal work of tower to be 1/10th of the capacitance of the insulator.

Solution: The arrangement is shown in the Fig. 5.5.2.

Applying Kirchhoff's current law at node P,

 

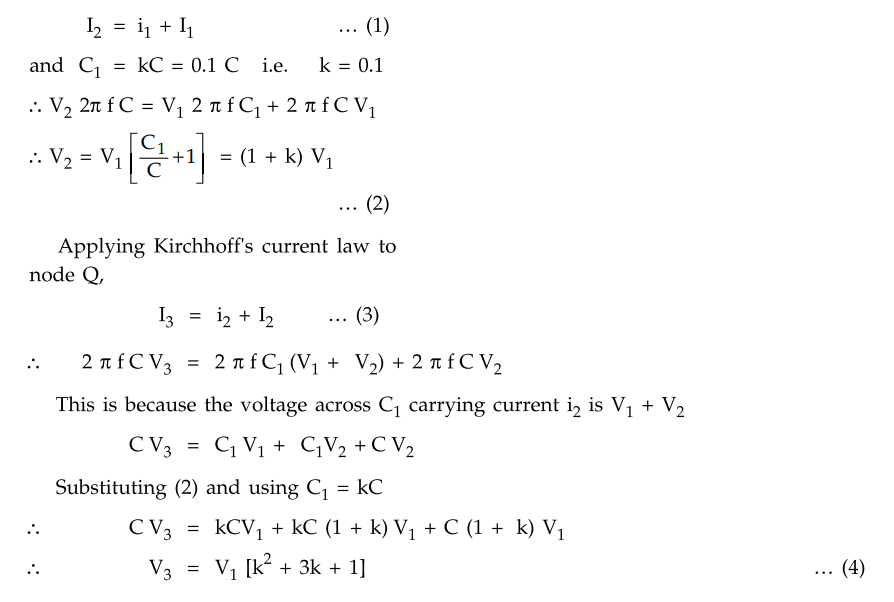
Now V₃ is voltage across line unit which is closest to the line conductor, given as 20 kV.

It can be noted that if the capacitance between insulator and line conductor is neglected then the equations for the voltage distribution across the insulators of a string remain same as derived and can be used directly to solve the problems.

 

Example 5.5.2 An insulator string consists of three units, each having a safe working voltage of 15 kV. The ratio of self to shunt capacitance is 6:1. Find the maximum safe working voltage of the string and the string efficiency.

AU : April-99, Oct.-Ol, April-05, May-11, 12, Dec.-17, Marks 16

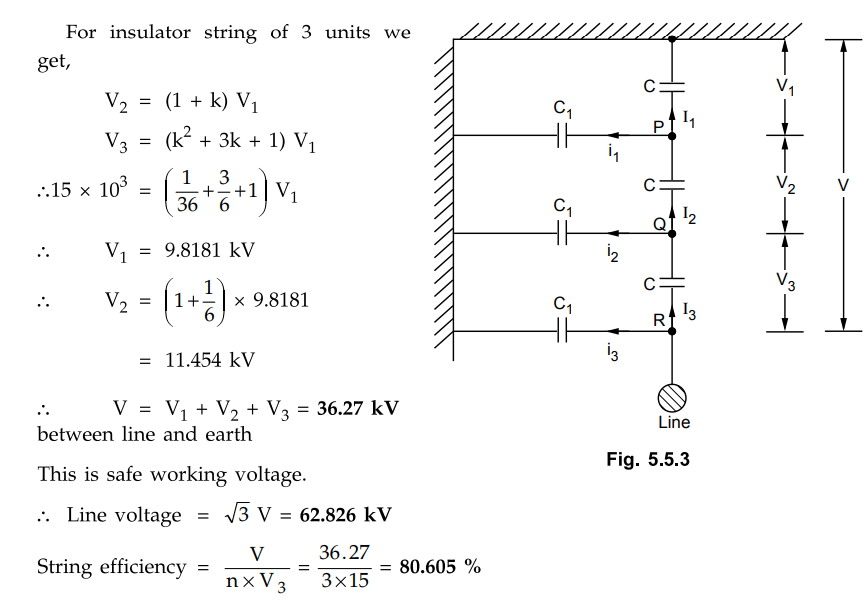
Solution : Let C₁ = shunt capacitance and C = Self capacitance

C / C₁  = 6 / 1

C₁ = 1/6 C   i.e. k = 1/6  = 0.1667

Let voltage across line unit be 15 kV which is its safe working voltage i.e.V₃ = 15 × 10³ V. This is because the maximum voltage appears across the line unit. 

For insulator string of 3 units we get,

 

Example 5.5.3 An insulator string for 66 kV line has 4 discs. The shunt capacitance between each joint and metal work is 10 % of the capacitance of each disc. Find the voltage across the different discs and string efficiency.

Solution : Let = Shunt capacitance and C = Self capacitance

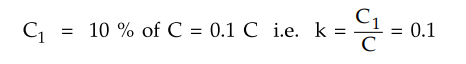
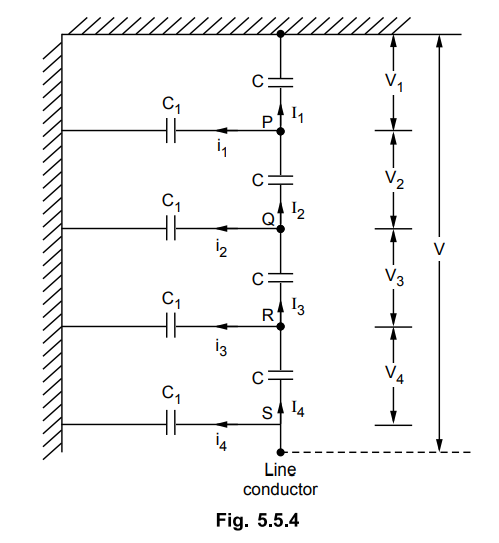
The arrangement of disc is shown in the Fig. 5.5.4.

Example 5.5.4 In a 33 kV overhead line, there are three units in the string of insulators. If the capacitance between each insulator pin and earth is 11 % of self capacitance of each insulator, find the distribution of voltage over 3 insulators and string efficiency. Draw the equivalent circuit.

Solution : Let, C₁ = Shunt capacitance

C = Self capacitance

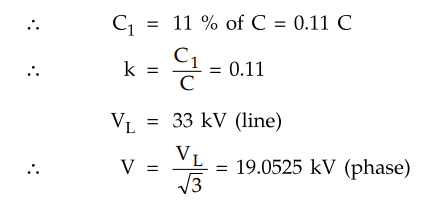
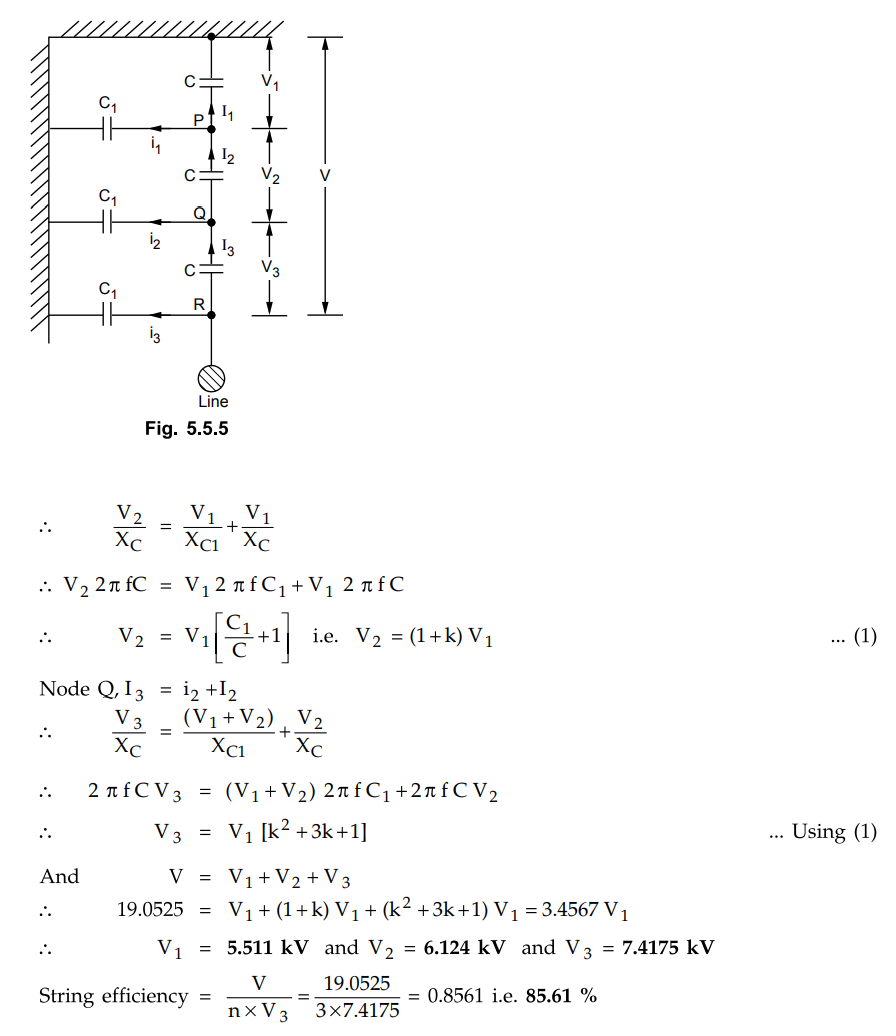
Applying KCL at various nodes P, Q and R.

 

Example 5.5.5 In a 3 unit insulator, the joint to tower capacitance is 20 % of the capacitance of each unit. By how much should the capacitance of the lowest unit be increased to get a string efficiency of 90 % ? The remaining two units are left unchanged.

AU : May-15, Marks 16

Solution : The arrangement is shown in the Fig. 5.5.6.

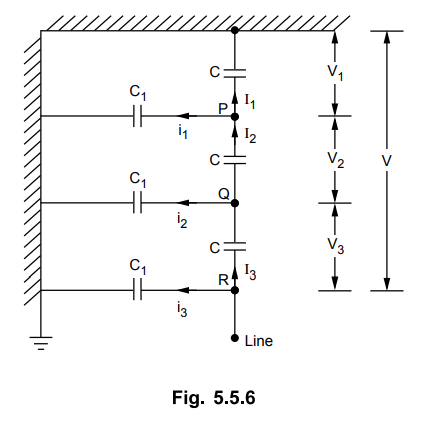
C₁ = 0.2 C, k = 0.2

Applying KCL at node P,

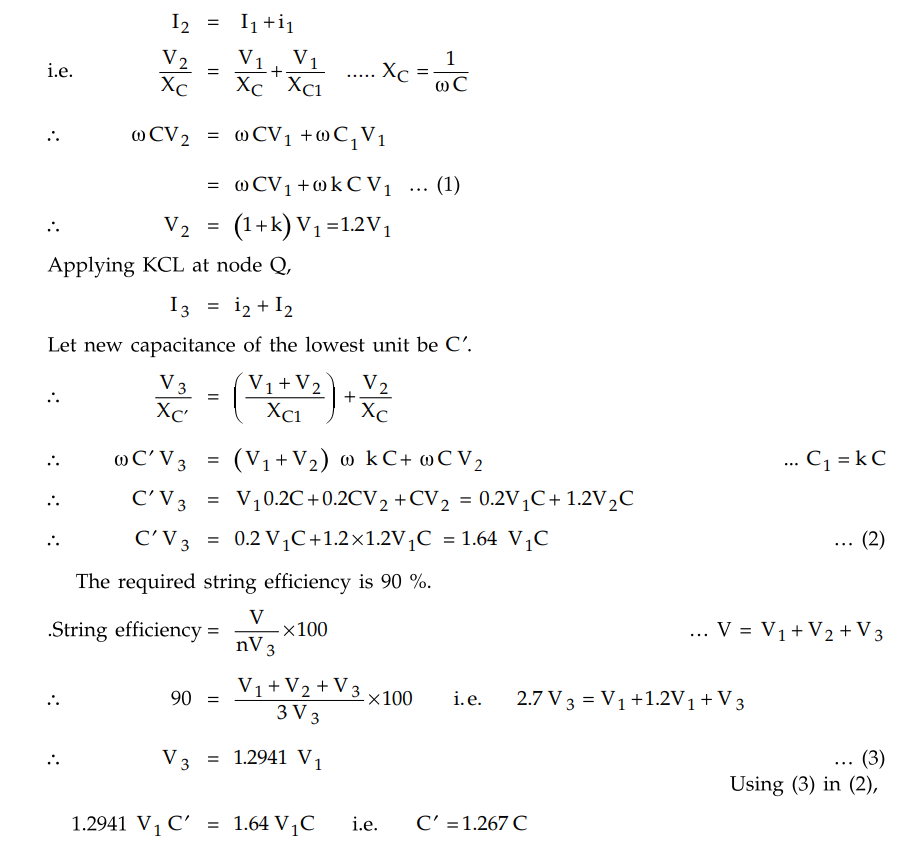
Thus the initial capacitance of last unit C is to be increased to 1.267 C to get string efficiency of 90 %. Hence increase in the capacitance of the third unit is 0.267 i.e 26.7 %. 

 

Example 5.5.6 A string of 6 insulator units has self capacitance equal to 10 times the pin to earth capacitance. Find

a) Voltage distribution from top to bottom insulator as a percentage of the total voltage.

b) The string efficiency.

Solution : The arrangement is shown in the Fig. 5.5.7.

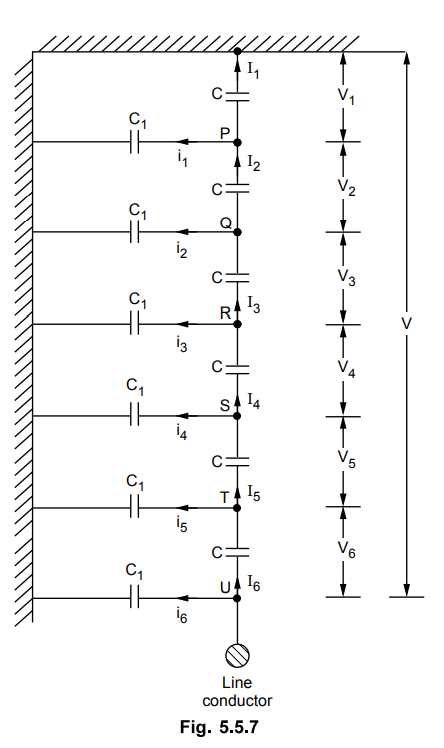
Let C₁ = Shunt capacitance and

C = Self capacitance

C = 10 C₁

C₁ = kC = 0.1 C

k = 0.1

Applying KCL at various nodes,

 

Example 5.5.7 In a 5 insulator disc string, capacitance of each unit and earth is 1th / 6 of the mutual capacitance. Find the voltage distribution across each insulator in the string, as a percentage of voltage of conductor to earth. Find also the string efficiency.

Solution : The string is shown in the Fig. 5.5.8.

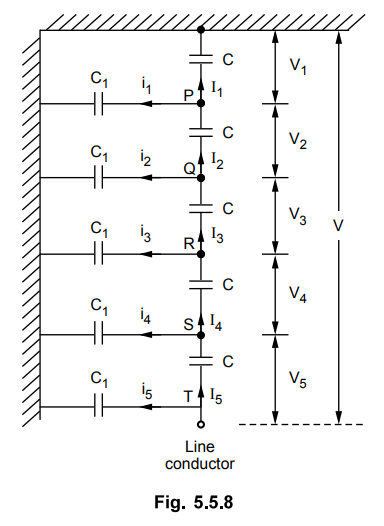
C₁ = kC = 1/6 C

Applying KCL at various nodes P, Q, R and S and using, 

 

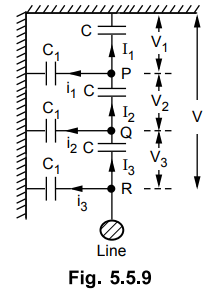
Example 5.5.8 A 3 phase overhead transmission line is being supported by three disc insulators. The potentials across top unit and middle unit are 9 kV and 11 kV respectively. Calculate (i) the ratio of capacitance between pin and earth to the self-capacitance of each unit (ii) the line voltage and (iii) string efficiency.

AU : Dec.-11,Marks 16

Solution :

The arrangement is shown in Fig. 5.5.9.

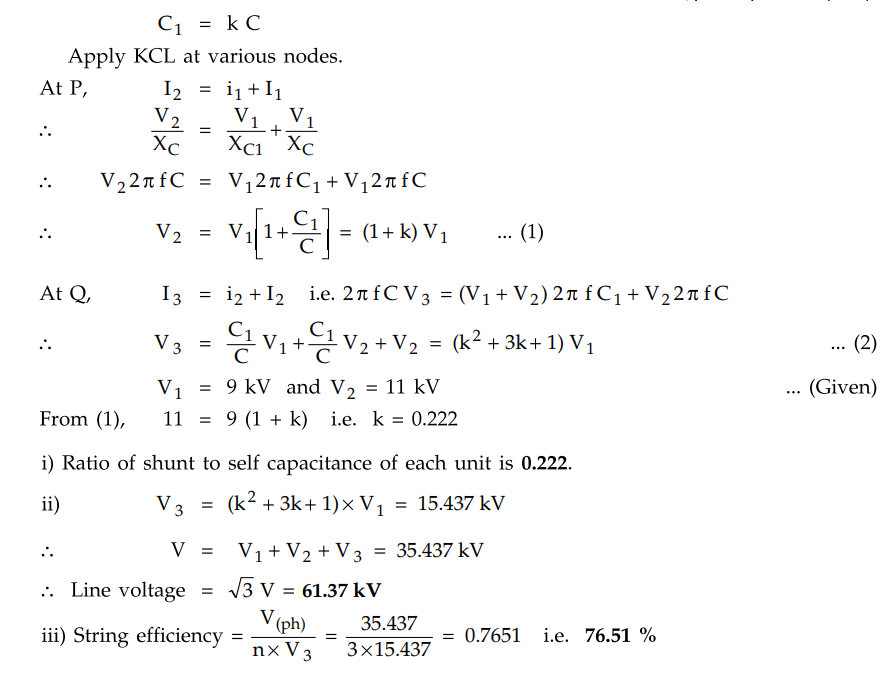
Review Questions

1. Define string efficiency.

2. Derive the expression for the string efficiency of a 3 disc string.

3. Explain the procedure cf calculating the string efficiency of a 4 unit string.

4. Considering a suspension insulator string of 4 units, obtain expressions for the voltages across various units in terms of V₁ the voltage across the top most unit and m is the ratio between ground capacitance and mutual capacitance.

[Ans.: V₂ = V₁ (l + m), V₃ = V₁ (m² +3m +l), V₄ = V₁(m³ + 5m² + 6m +1)] 

5. Each line of a 3 phase system is suspended by a string of 3 similar insulators. If the voltage across the bottom most unit (line unit) is 17.5 kV, calculate the voltage across the insulator string. Also find the string efficiency. Assume that the earth capacitance is 1th/8 of mutual capacitance.        

[Ans: 44.241 kV, 84.268 %]

6. A three phase overhead transmission line uses suspension insulator using 3 insulator units. The voltage across the top unit is 10 kV and that across the middle unit is 11 kV. Calculate,

i. Ratio of shunt to self capacitance ii. String efficiency iii. Line voltage

[Ans.: 0.1,86.7 %, 59 kV]

7. Each line cf a three phase system is suspended by a string of 3 similar units. If the voltage across the line unit is 22 kV, calculate the line to neutral voltage and string efficiency. Assume that the shunt capacitance between each insulator and earthed metal work of tower to be l/8th of the capacitance cf the insulator.        

[Ans.: 55.6175 kV, 84.26 %]

8. Three busbar conductors in outdoor substation supplied by the units of post insulators. Each unit consists of stack of 3 pin insulators. The voltage across line unit is 9 kV while that across middle unit is 7.5 kV. Find the busbar voltage of station.        

[Ans.: 39.9019 kV]