Superposition Theorem

SUPERPOSITION THEOREM

Statement

"In a linear network containing several sources (including dependent sources), the over all response (branch current or voltage) in any branch in the network equals the algebraic sum of the responses of each individual source considered separately with all other sources made inoperative. i.e replaced by their internal resistances or impedances".

To make a source inoperative, it is short circuited leaving behind its internal resistance or impedance, if it is a voltage source and it is open circuited leaving behind its internal resistance or impedance, if it is a current source.

Proof

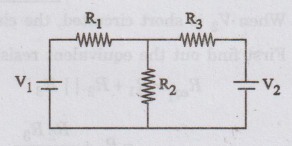
Consider a simple circuit consisting of two voltage sources E₁ or V₁ and E₂ or V₂.

To calculate current passing through R₂, we can follow either mesh analysis or superposition theorem.

Mesh analysis

By inspection method

Superposition theorem

Current flow through R₂ due to V₁ and V₂ = 0

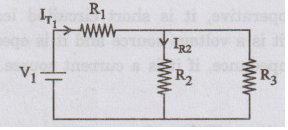
When V₂ is short circuited, the circuit becomes

First find out the equivalent resistance of the above circuit.

According to Superposition theorem the current passing through R2 due to voltage source V₁ and V₂ is the sum of the currents passing through R2 due to individual voltage sources V₁ and V₂.

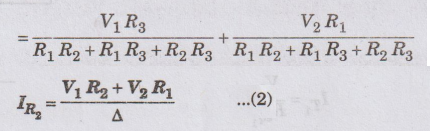
where Δ = R₁ R₂ + R₁ R₃ + R₂ R₃

Equations (1) & (2) are the same. Thus, Superposition theorem is verified. This theorem is valid only for linear systems. This theorem can be applied for calculating the current through or voltage across a particular element. But, this Superposition theorem is not applicable for calculation of power.

 

EXAMPLE 1: Solve for current through 52 resistor by principle of Superposition theorem.

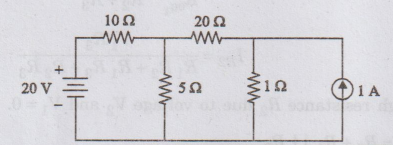
Solution :

First, convert current source into equivalent voltage source.

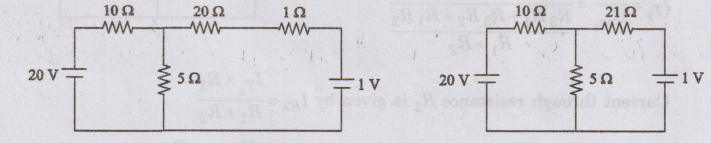
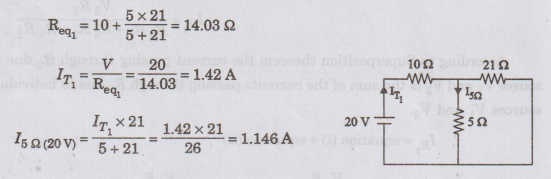
Step 1

1_5Ω due to 20V alone (1 V source is short circuited)

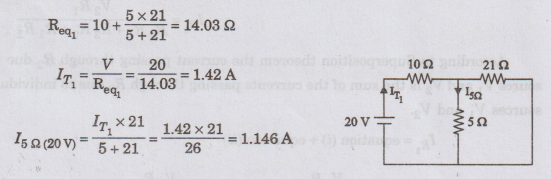
Step 2

I_5Ω due to 1 V alone (20 V source is short circuited)

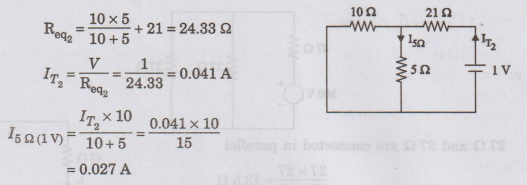
Step 3

According to superposition theorem current passing through 5 Ω resistance due to 20 V and 1 V sources is

I_5Ω - I_5Ω (20 V) + I_5Ω (1V)

= 1.146+0.027 = 1.173 A

I_5Ω  = 1.173 A

 

EXAMPLE 2: Using Superposition theorem, find the current I_L and the power consumed by 23 Ω resistor in the circuit shown in figure.

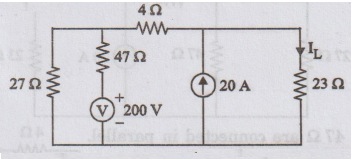
Solution :

First, open circuit the current source. Now, the circuit becomes

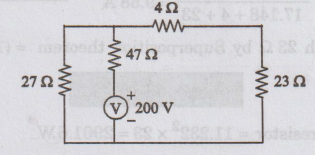
Now current through 27 Ω resistor is obtained as follows.

4 Ω and 23 Ω are connected in series.

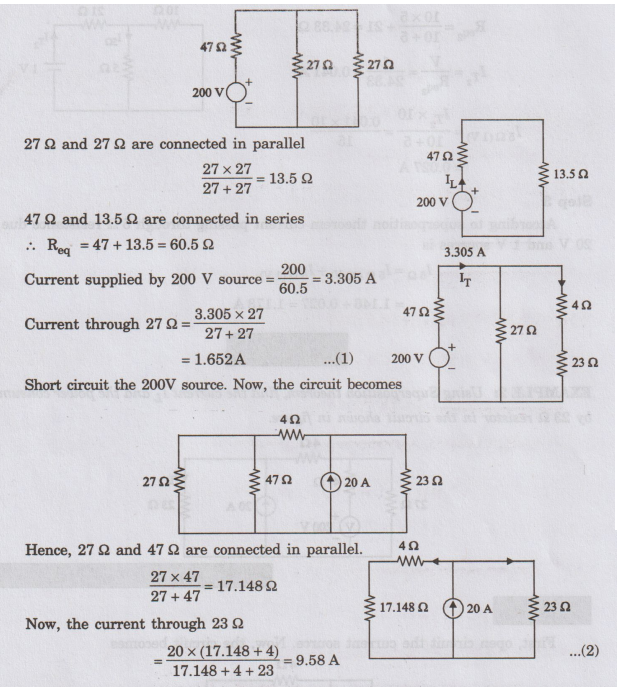
The total current through 23 Ω by Superposition theorem = (1.652 +9.58) A

I_23Ω =11.232 A

Power in the 23 Ω resistor = 11.232² ×  23 = 2901.6W

 

EXAMPLE 3: Calculate the power dissipated in the 4 2 resistor given in network, using Superposition theorem.

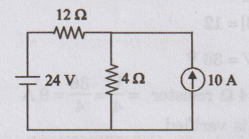
Solution

Step I:

Current source should be open circuited. Now, the circuit becomes

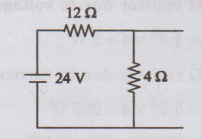
Now, the current flowing through 4 2 resistor = 24 / 12 + 4 = 1.5 A  …. (i)

Step II:

The voltage source is short circuited. Now, the circuit becomes

The current flowing through 4 Ω

= 10 × 12 / 12 + 4 = 7.5 A ….. (ii)

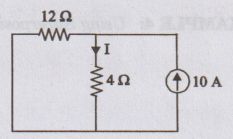
Step III:

The total current flowing through 4Ω = 1.5 + 7.5 = 9 A

The same circuit is analysed by nodal method to verify superposition theorem.

Applying nodal analysis

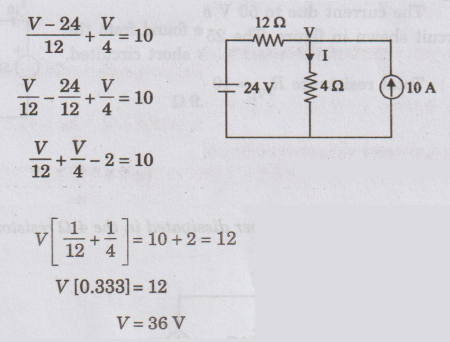
V = 36 V

The current passing through the 4 Ω resistor = V / 4 = 36 /  = 9A

Thus, the Superposition theorem is verified.

Power dissipated in the 4Ω resistor when both the sources are acting simultaneously is given by

P = 9² × 4 =324 W

ed bloode sos

Power dissipated in the 4 Ω resistor due to voltage source acting alone.

P₁ =I²R = 1.5² × 4 = 9W

Power dissipated in the 4 Ω resistor due to current source acting alone.

P₂ = I²R = 7.52 × 4 = 225 W

From the above results, the Superposition of P1 and P2 gives

= 9 + 225 = 234 W

which is not equal to P = 324 W

From this result, the Superposition theorem is not valid for power responses. It is mainly used for calculating voltage and current responses.

 

EXAMPLE 4: Using Superposition principle, find the current in each resistor of given figure.

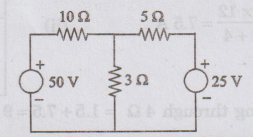
Solution :

The current due to 50 V source can be found from the circuit shown in figure. The 25 V source is short circuited.

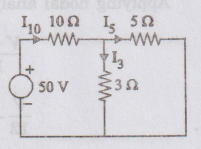
Total resistance R_eq1 = 10 + 5 × 3 / 5+3 = 11.9 Ω

The current due to the 25 V source can be found from the circuit shown in figure. 50 V source is short circuited.

When both sources are acting, the directions of current are shown in figure.

 

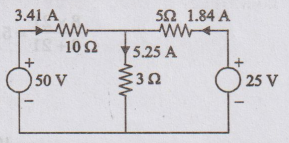
EXAMPLE 5: Using Superposition theorem, find the current in 10 2 resistor of the network shown in figure.

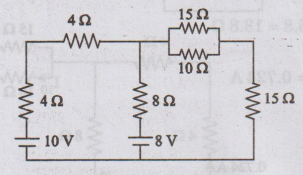
Solution

First, 10 V source is acting alone. 8 V source is short circuited. Now, the circuit

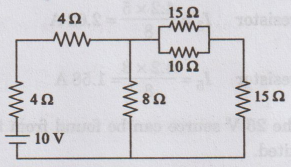
becomes

Then, find the equivalent resistance R_eq of the circuit 4 Ω and 4 Ω are connected in series.

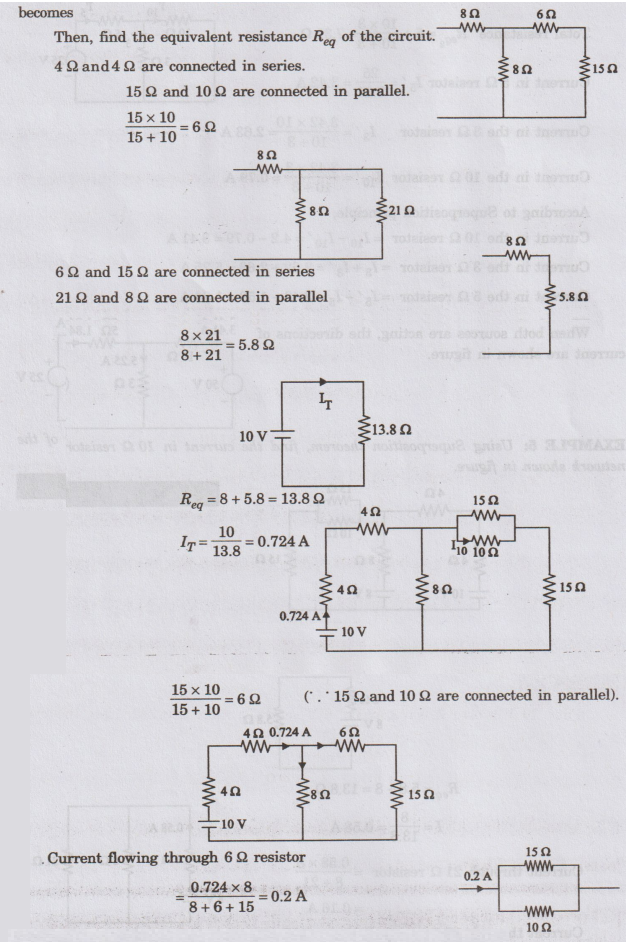
Current flowing through 6 Ω resistor

= 0.724 × 8 / 8 + 6 + 15 = 0.2 A

Currentthrough 10 Ω resistor (due to 10 V) = 0.2 × 15 / 15 + 10 = 0.12 A

Now, 8 V source is acting alone, 10 V source is short circuited. Now, the circuit becomes

 

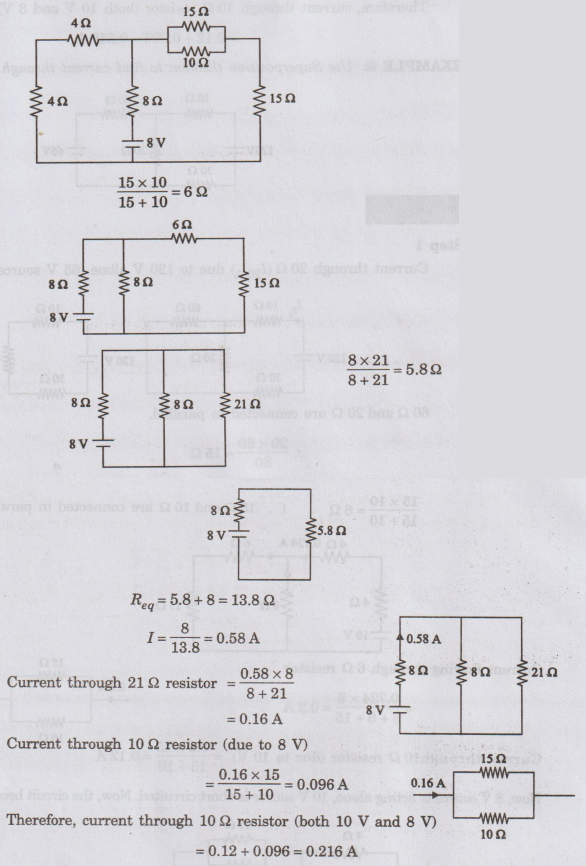
EXAMPLE 6: Use Superposition theorem to find current through 20 2 resistance.

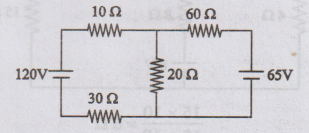
Solution :

Step 1

Current through 20 Ω (I_{20 Ω}) due to 120 V alone (65 V source is short circuited)

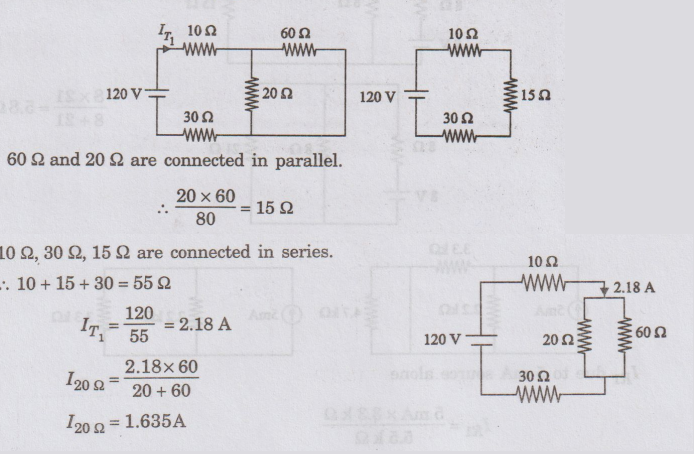
Step 2

Current through 20 Ω due to 65 V alone (120 V source is short circuited)

Step 3

According to Superposition theorem current flowing through 202 resistance due to 120 V and 65 V sources is I_20Ω = 1.635 + 0.59 = 2.225 A

I_20Ω = 2.225 A

 

EXAMPLE 7: Using Superposition theorem, find the current through R1 for the given network.

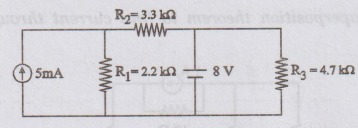
Solution :

Step 1

Considering current source alone with voltage source short circuited.

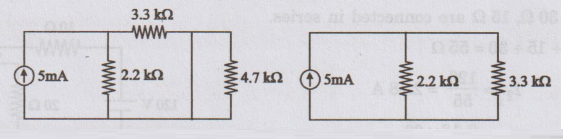
I_R1 due to 5 mA source alone

I_R1 = 5 mA × 3.3 kΩ / 5.5 k Ω

I_R1 = 3 mA

Step 2

I_R1 due to 8 V source alone (5 mA source is open circuited)

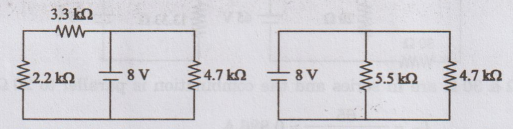
In a parallel circuit, the voltage across the parallel branches is the same. So,

I _{5.5 kΩ} = 8 / 5.5 k Ω = 1.454 mA

I_R1(8V) = I _{2.2 k Ω} = I_{5.5 k Ω} = 1.454 mA

According Superpositiortheorem,

I_R1 = 1.454 mA + 3 mA

I_R1 = 4.454 mA

 

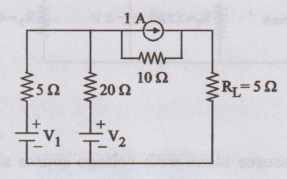
EXAMPLE 8: Use Superposition theorem to find current through R_L in the network given V₁ V₂ = 10 V.

Solution:

Step - I

V₁ alone is acting; V₂ is short circuited; 1 A is open circuited.

Step - 2

V₂ alone is acting; V₁ is short circuited; 1 A is open circuited.

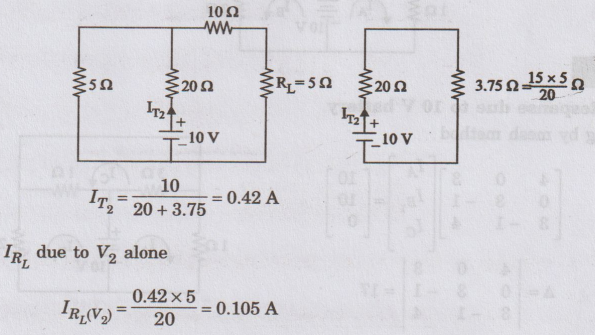
Step - 3

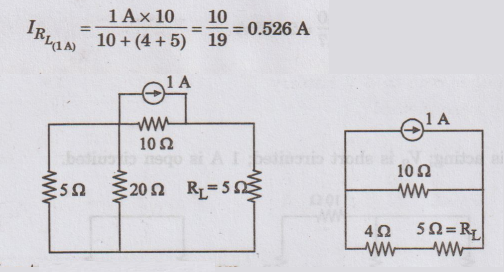
According to Superposition theorem,

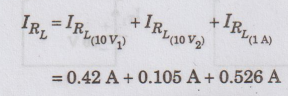
I_RL = 1.05 A

 

EXAMPLE 9: Find the current in the 22 resistor by the principle of Superposition.

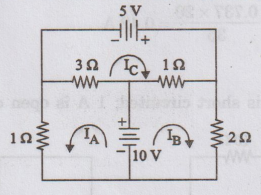
Solution:

Step 1: Response due to 10 V battery

Solving by mesh method

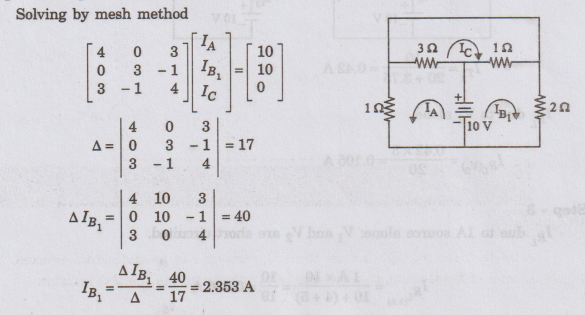
Step 2: Response due to 5 V battery

Solving by mesh method

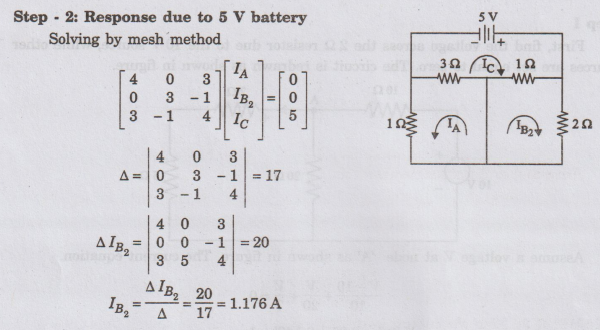
Current through the 2 Ω resistor is

I_B = I_B1 + I_B2 = 2.353 + 1.176

I_{2 Ω} = 3.53 A

 

EXAMPLE 10: Find the voltage across the 22 resistor in figure by using the Superposition theorem.

Solution :

Let us find the voltage across the 2 Ω resistor due to individual sources. The algebraic sum of these voltages gives the total voltage across the 2 Ω resistor.

Step I

First, find the voltage across 2 Ω resistor due to the 10 V source, while other sources are set equal to zero. The circuit is redrawn as shown in figure.

Step II

Next, find out the voltage across the 2 Ω resistor due to the 20 V  source, while the other sources are set equal to zero. The circuit is redrawn as shown in figure

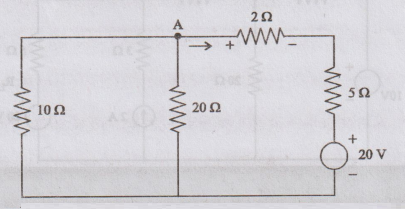
Assuming voltage V at node ‘A’ as shown in figure. The current equation is

V – 20 / 7 + V / 20 + V / 10 = 0

V[0.143 + 0.05 + 0.1] = 2.86

V = 2.86 / 0.293 = 9.76 V

The voltage across the 2 Ω resistor  due to the 20 V source is

V² = (V-20/7) × 2 = -2.92 V

= 0.73 x 2 = 1.46 V

Step III

Next, find the voltage across the 2 Ω resistor due to the 2 A current source, while the other sources are set equal to zero. The circuit is redrawn as shown in figure

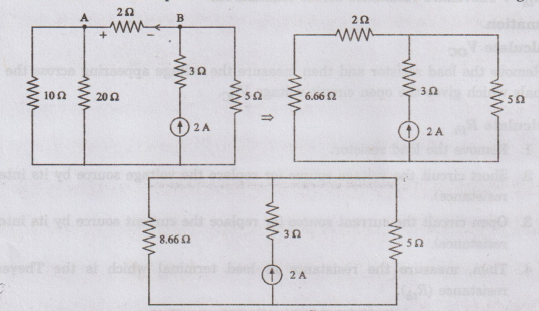
The current through 2 Ω resistor = 2 × 5 / 5 + 8.66 = 0.73 A

The voltage across the 2 Ω resistor = 0.73 × 2 = 1.46 V

The algebraic sum of these voltages gives the total voltage across the 2 Ω resistor in the network.

V = 0.97 - 2.92 + 1.46 - 0.49 V

The negative sign of the voltage indicates that the voltage at 'A' is negative.