Surge Impedance

Surge Impedance

In power system work, the characteristic impedance is sometimes referred as surge impedance. It is defined as square root of Z/Y where

Z = Series impedance of line = R + jX

Y - Shunt admittance of line = G + jB

The term surge impedance is normally reserved for the special case of a lossless line. For a lossless line, its resistance and conductance are zero. Thus the characteristic impedance reduces to √L/C which is nothing but a pure resistance in terms of dimensions. Its value is normally 400 to 600 Ω for an overhead line while for underground cable its value is typically between 40 to 60 Ω.

The surge impedance of the line can be determined in terms of Z_OC and Z_SC where Z_OC and Z_SC are impedances measured at sending end with the receiving end open circuited and short circuited respectively.

When dealing with high frequencies or with surges due to lightning, losses are often neglected and the surge impedance becomes important.

1. Surge Impedance Loading (SIL)

The Surge Impedance Loading (SIL) of a line is the power delivered by a line to a purely resistive load equal to its surge impedance. The line is assumed to have no resistance. With such loading, the current will be

where |V_R| is the line to line voltage at the load.

As the load is purely resistive we have,

SIL is also called natural power of the line. Sometimes it is convenient to express the power transmitted by a line in terms of per unit of SIL which is the ratio of the power transmitted to the surge impedance loading. 

The permissible loading of a transmission line may be expressed as a fraction of its SIL and SIL provides a comparison of load carrying capabilities of lines.

If surge impedance, Z_C = 400 Ω then

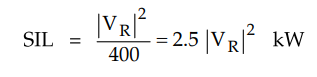
The above equation puts limit on the maximum power that can be delivered which is helpful in designing the transmission lines.

By increasing the value of receiving end voltage, the power transmitted through long transmission line can be increased. It can also be increased by using more than one transmission lines in parallel. But the method is costly. Hence for increasing SIL, V_R is increased or Z_C is decreased.

Review Question

1. Explain the concept of surge impedance loading.