Synchronous Impedance Method or E.M.F. Method

Synchronous Impedance Method or E.M.F. Method AU : Oct.-95, 98, 99, Dec.-04, 06, 07, 12, 14, May-04, 08, 10, 14,

The method is also called E.M.F. method of determining the regulation. The method requires following data to calculate the regulation.

1. The armature resistance per phase (R_a).

2. Open circuit characteristics which is the graph of open circuit voltage against the field current. This is possible by conducting open circuit test on the alternator.

3. Short circuit characteristics which is the graph of short circuit current against field current. This is possible by conducting short circuit test on the alternator. 

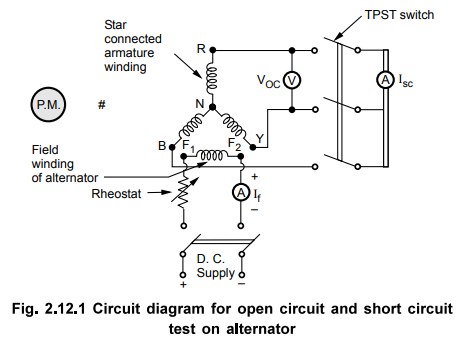
Let us see, the circuit diagram to perform open circuit as well as short circuit test on the alternator. The alternator is coupled to a prime mover capable of driving the alternator at its synchronous speed . the armature is connected to the switch. The other terminals of the switch are short circuited through an ammeter. The voltmeter is connected across the lines to measure the open circuit voltage of the alternator.

The field winding is connected to a suitable d.c. supply with rheostat connected in series. The field excitation i.e. field current can be varied with the help of this rheostat. The circuit diagram is shown in the Fig. 2.12.1.

 

1. Open Circuit Test

Procedure to conduct this test is as follows :

i) Start the prime mover and adjust the speed to the synchronous speed of the alternator.

ii) Keeping rheostat in the field circuit maximum, switch on the d.c. supply.

iii) The T.P.S.T. switch in the armature circuit is kept open.

iv) With the help of rheostat, field current is varied from its minimum value to the rated value. Due to this, flux increases, increasing the induced e.m.f. Hence voltmeter reading, which is measuring line value of open circuit voltage increases. For various values of field current, voltmeter readings are observed.

The observations for open circuit test are tabulated as below :

Observation table for open circuit test :

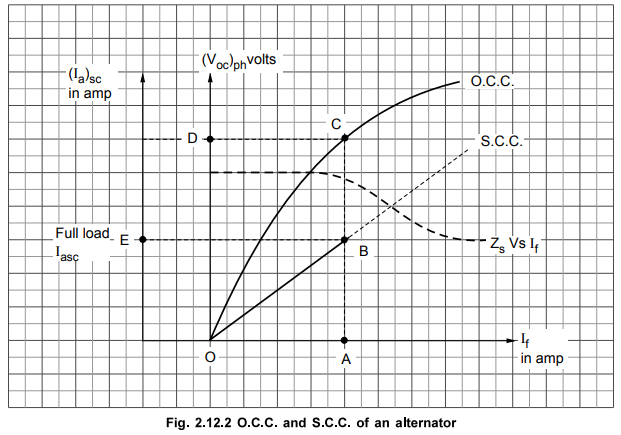
From the above table, graph of (V_oc)ph against I_f is plotted.

Key Point : This is called open circuit characteristics of the alternator, called O.C.C. This is shown in the Fig. 2.12.2

 

2. Short Circuit Test

After completing the open circuit test observations, the field rheostat is brought to maximum position, reducing field current to a minimum value. The T.P.S.T. switch is closed. As ammeter has negligible resistance, the armature gets short circuited. Then the field excitation is gradually increased till full load current is obtained through armature winding. This can be observed on the ammeter connected in the armature circuit. The graph of short circuit armature current against field current is plotted from the observation table of short circuit test. This graph is called Short Circuit Characteristics, S.C.C. This is also shown in the Fig. 2.12.2.

Observation table for short circuit test :

The S.C.C. is a straight line graph passing through the origin while O.C.C. resembles B-H curve of a magnetic material.

Key Point : As S.C.C. is straight line graph, only one reading corresponding to full load armature current along with the origin is sufficient to draw the straight line.

 

3. Determination of Z_s from O.C.C. and S.C.C.

The synchronous impedance Z_s of the alternator changes as load condition changes. O.C.C. and S.C.C. can be used to determine Z_s for any load and load p.f. conditions.

In short circuit test, external load impedence is zero. The short circuit armature is circulated against the impedance of the armature winding which is Z_S. The voltage responsible for driving this short circuit current is internally induced e.m.f. This can be shown in the equivalent circuit drawn in the Fig.2.12.3.

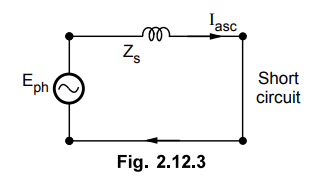
From the equivalent circuit we can write,

Z_s = E/I_asc

Now value of I_asc is known, which can be observed on the ammeter. But internally induced e.m.f. can not be observed under short circuit condition. The voltmeter connected will read zero which is voltage across short circuit. To determine Z_s it is necessary to determine value of E which is driving Iasc against Z_s.

Now internally induced e.m.f. is proportional to the flux i.e. field current I_f.

E_ph oc ϕ oc  I_f        ... From e.m.f. equation

So if the terminals of the alternator are opened without disturbing I_f which was present at the time of short circuited condition, internally induced e.m.f. will remain same as Eph. But now current will be zero. Under this condition equivalent circuit will become as shown in the Fig. 2.12.4.

It is clear now from the equivalent circuit that as I_a = 0 the voltmeter reading (V_oc)ph will be equal to internally induced e.m.f. (E_ph).

E_ph = (V_oc)_ph on open circuit 

This is what we are interested in obtaining to calculate value of Zs. So expression for Z_S can be modified as,

So O.C.C. and S.C.C. can be used effectively to calculate Z_S.

The value of Z_S  is different for different values of I_f as the graph of O.C.C. is non linear in nature.

So suppose Z_S at full load is required then,

I_asc = Full load current

From S.C.C. determine I_f required to drive this full load short circuit Ia. This is equal to 'OA', as shown in the Fig. 2.12.2.

Now for this value of I_f, (Voc)ph can be obtained from O.C.C. Extend line from point A, till it meets O.C.C. at point C. The corresponding (V_oc)_ph value is available at point D.

General steps to determine Z_S at any load condition are :

i) Determine the value of (I_asc) ph for corresponding load condition. This can be determined from known full load current of the alternator. For half load, it is half of the full load value and so on.

ii) S.C.C. gives relation between (I_asc) _ph and I_f. So for (Iasc) ph required, determine the corresponding value of I_f from S.C.C.

iii) Now for this same value of I_f, extend the line on O.C.C. to get the value of (V_oc)_ph This is (V_oc)_ph for same I,, required to drive the selected (I_asc)_ph

iv) The ratio of (V_oc) ph and (I_asc) _ph, for the same excitation gives the value of Z_S at any load conditions.

The graph of synchronous impedance Z_S against excitation current I_f is also shown in the Fig. 2.12.2. 

 

4. Regulation Calculations

From O.C.C. and S.C.C., Z_s can be determined for any load condition.

The armature resistance per phase (R_a) can be measured by different methods. One of the method is applying d.c. known voltage across the two terminals and measuring current. So value of R_a per phase is known.

So synchronous reactance per phase can be determined.

No load induced e.m.f. per phase, E_ph can be determined by the mathematical expression derived earlier.

where  V_ph = Phase value of rated voltage

I_a = Phase value of current depending on the load condition

cos ϕ = p.f. of load

Positive sign for lagging power factor while negative sign for leading power factor, R_a and X_S values are known from the various tests performed.

The regulation then can be determined by using formula,

Regulation E_ph – V_ph / V_ph × 100

 

5. Advantages and Limitations of Synchronous Impedance Method

The main advantage of this method is the value of synchronous impedance Z_S for any load condition can be calculated. Hence regulation of the alternator at any load condition and load power factor can be determined. Actual load need not be connected to the alternator and hence method can be used for very high capacity alternators.

The main limitation of this method is that the method gives large values of synchronous reactance. This leads to high values of percentage regulation than the actual results. Hence this method is called pessimistic method.

The synchronous impedance is practically variable and not constant. If there is saturation, it remains constant but it decreases towards the saturation while it increases for the low saturation region. In synchronous impedance method, in short circuit test, the field current required is very small to pass the short circuit current hence the flux density is low and the region is low saturation region. Hence the synchronous impedance is much higher than its normal value. Thus the drop I_aZ_s is high due to which the regulation is also high than the actual value, by synchronous impedance method. Hence the method is called pessimistic.

Example 2.12.1 The open circuit and short circuit test is conducted on a 3 phase, star connected, 866 V, 100 kVA alternator.

The O.C. test results are,

The field current of 1 A, produces a short circuit current of 25 A.

The armature resistance per phase is 0.15 Ω. Calculate its full load regulation at

0.8 lagging power factor condition.

 

Solution :

For calculation of Z_s on full load, it is necessary to plot O.C.C. and S.C.C. to the scale.

Note : If for same value of I_f, both I_asc and V_oc can be obtained from the table itself, graph need not be plotted. In some problems, the values of V_oc and I_asc for same If are directly given, in that case too, the graph need not be plotted.

In this problem, I_asc = 25 A      for I_f = 1 A.

But we want to calculate Z_s     for I_asc = Its full load value which is 66.67 A.

So graph is required to be plotted.

For plotting O.C.C. the line values of open circuit voltage are converted to phase by dividing each value by √3.

From S.C.C., For I_asc = 66.67 A, If = 2.4 A

From O.C.C., For I_f = 2.4 A, (V_oc) = 240 V

 

Example 2.12.2  A 3 ph, 1500 kVA, star connected 50 Hz, 2300 V alternator has a resistance between each pair of terminals as measured by direct current is 0.16 Q. Assume that the effective resistance is 1.5 times the ohmic resistance. A field current of 70 A produces a short circuit current equal to full load current of 376 A in each line. The same field current produces an emf of 700 V on open circuit. Determine the synchronous reactance of the machine and its full load regulation at 0.8 pfi lag.

Solution :

1500 kVA, V_L = 2300 V

From the Fig. 2.12.6, R_a = 0.08 Ω /ph

R_a (effective) = 1.5 × 0.08 Ω /ph

.-. R_a = 0.12 Ω / ph

I_asc = 376 A for I_f = 70 A and V_oc (line) = 700 V

For star connection, line current is same as phase current.

 

Example 2.12.3 Calculate from the observations taken on a 125 kVA, 400 V, 3 phase alternator, the % regulation for half load condition at 0.8 leading pfi O.C. Test observation :

While full load current is obtained on short circuit condition at a field current of 8 A. Assume star connection and R_a = 0.1 Ω/ph. The short circuit current variation with respect to field current is linear. 

Solution :

VL = 400 V, kVA = 125

kVA = √3 V_L I_L × 10^-3

125= √3 × 400 × I_L × 10^-3

I_L = 180.42 A This is full load current

I_aph = 180.42 A on full load.

Now I_f = 8 A to get I_asc = I_a full load and as I_f against I_asc is linear variation to get half load current on short circuit, the I_f required is

8/2 = 4 A

The graph need not be plotted but shown to clear the calculations. Now referring to O.C. Test observations, without plotting graph we can get Voc value for I_f = 4 A, which is 140 V. 

 

Example 2.12.4 From the following test results, determine the voltage regulation fcy E.M.F. method of a 2000 V, 1 phase alternator delivering a current of 100 A at i) Unity p.f; ii) 0.8 leading p.f; and iii) 0.71 lagging p.f. Test results : full load current of 100 A is produced on short circuit by a field excitation of 2.5 A. An e.m.f. of 500 V is produced on open circuit by the same excitation. The armature resistance is 0.8 Ω.

Solution : Note that the given alternator is single phase hence all the voltage and currents are obviously per phase and there is no question of line values.

 

Example 2.12.4 A 3-phase, star-connected, 1000 kVA, 11,000 V alternator has rated current if 52.5 A. The ac resistance of the winding per phase is 0.45 Ω. The test results are given below :

OC Test : field current = 12.5 A, voltage between lines = 422 V.

SC Test : field current = 12.5 A, line current = 52.5 A

Determine the full load voltage regulation of the alternator

i) 0.8 pf lagging and ii) 0.8 pf leading.

Solution :

1000 kVA, V_L = 11000 V, R_a = 0.45 Ω

 

Examples for Practice

Example 2.12.6 A 2300 V, 50 Hz, 3 phase star connected alternator has an effective armature resistance of 0.2 Ω. A field current of 35 A produces a current of 150 A on short circuit and an open circuit emf 780 V (line). Calculate the voltage regulation at 0.8 p.f. lagging and 0.8 p.f. leading for the full load current of 25 A.

[Ans.: 3.773 %, - 2.924 %]

Example 2.12.7 The open and short circuit test readings for a 3 ϕ - star connected 1000 kVA, 2000 V - 50 Hz synchronous generator are,

The armature effective resistance is 0.2 ohm per phase. Draw the characteristic curves and estimate the full load percentage regulation i) 0.8 pf lagging ii) 0.8 power factor leading.

[Ans.: i) % Reg. = 91.18 %, ii) % Reg. = - 9.29 %]

Example 2.12.8 A 600 V, 60 kVA, single-phase alternator has an effective resistance of 0.2 Ω. A field current of 10 A produces an armature current of 210 A on short-circuit and an e.m.f. of 480 V on open-circuit.

Calculate :

1) Synchronous impedance and reactance

2) Regulation with 0.8 p.f. lagging, unity and 0.6 p.f. leading.

VTU : March-07, Aug.-07

[Ans.: 2.2857 Ω 2.2769 Ω, 28.6 %, 10.08 %, - 23.97 %]

Example 2.12.9 The effective resistance of a 2.2 kV, 50 Hz, 440 kVA, single phase alternator is 0.5 Ω. On short circuit a field current of 40 A gives a full load current of 200 A. The emf on open circuit with the same field excitation is 1.16 kV. Find the value of synchronous impedance and find the voltage regulation at full load and i) Unity power factor ; ii) 0.8 p.f. VTU : July-12

[Ans.: 17 %, 40.75 %]

Example 2.12.10 A 3 ph, 1500 kVA, star connected 50 Hz, 2300 V alternator has a resistance between each pair of terminals as measured by direct current is 0.16 Q. Assume that the effective resistance is 1.5 times the ohmic resistance. A field current of 70 A produces a short circuit current equal to full load current of 376 A in each line. The same field current produces an emf of 700 V on open circuit. Determine the synchronous reactance of the machine and its full load regulation at 0.8 p.f. lag. VTU : July-11

[Ans.; 1.0681 Ω / ph 22.88 %] 

Example 2.12.11 A 3 phase, 50 Hz, star-connected, 2000 kVA, 2300 V alternator gives a short circuit current of 600 A for a certain field excitation with the same excitation, the open circuit voltage was 900 V. The resistance between a pair of terminals was 0.12 Ω. Find the full load regulation at i) UPF and ii) 0.8 p.f. lagging.

[Ans.: 7.35 %, 23.91 %]

Example 2.12.12 A 100 kVA, 3000 V, 50 Hz, 3 phase star connected has effective armature resistance of 0.2 Ω. A field current of 50 A produces short circuit current of 250 A and open circuit emf of 1250 V. Calculate percentage regulation of 0.8 p.f. lagging and 0.6 p.f. leading. Draw the phasor diagram for both the conditions.

[Ans.: % Reg = - 2.4032 %]

Review Questions

1. Explain the synchronous impedance method (EMF method) of determining the regulation of an alternator.

2. Sketch and explain open circuit and short circuit characteristics of an alternator.

AU :May-10, Marks 8

3. Why synchronous impedance method is called pessimistic method ?