Tension and Sag at Erection

Tension and Sag at Erection

We have seen that there is major difference between the calculation of sag and tension in still air and the calculation of sag and tension under severe atmospheric conditions like ice coating, wind pressure etc. The factor of safety is provided for a particular tension and sag occurring at specific temperature and ice, wind conditions. These conditions are different than the conditions at the time of erection of the line.

So if the various values at maximum load conditions with ice, wind and at low temperature are known, then the corresponding values at the time of erection conditions without ice, wind and at normal temperatures, we must able to calculate.

So if the values are known at lowest temperature of - 5.5 °C then we must able to calculate all the values at the time of erection of line at (- 5.5 + t) °C. 

Let us revise the expressions for the various parameters derived earlier in the last section,

T = Tension = H

y = wx² / 2T where w = Weight of conductor

S = wl² / 2T  where  l = L/2  = Half span length

and c = l w²l³ / 6T²

where c = Actual half span length of conductor.

Let the values T₁, f₁, w₁, c₁, S₁,and t₁ are the known values of tension, stress, equivalent weight, half span conductor length, maximum sag and temperature respectively under severe conditions including ice and wind pressure and at - 5.5 °C.

T₁= f₁ × Area   where f₁ = Stress in kg/m²

While the values T₂, f₂, w₂, c₂, S₂,and t₂ are the values specified at normal erection conditions, without ice and wind pressure and at normal temperature t₂ which are to be calculated.

Let     a = Area of cross-section of conductor

α = Temperature coefficient of conductor at t₁ °C

E - Young's modulus

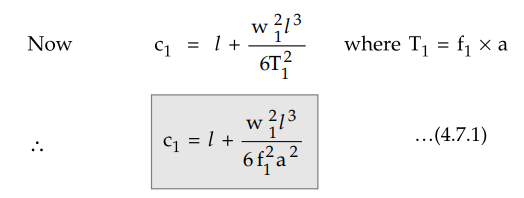
When the temperature increases from t₁ to t₂ then the wire gets elongated and the half span length of conductor changes from c₁ to c₂.

The increase in the length is given by c₁ (t₂ - t₁) α which can be approximated to (t₂ - t₁) α l

When the temperature changes from t₁ to t₂ the stress decreases from f₁ to f₂. Correspondingly there is reduction in the length of wire which is given by,

This is cubic equation in T₂ which can be solved to obtain tension at the time of erection.

Once T₂ is known, sag at erection time can be obtained as,

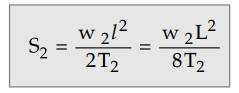
where w₂ = Weight of conductor without ice and wind.

Example 4.7.1 An overhead line has a span of 160 m of stranded copper conductor between level supports the sag is 3.96 m at - 5.5° C with 9.53 mm thick in ice coating and wind pressure of 40 kgf/m of projected area. Calculate the temperature at which the sag will remain the same under conditions of no ice and no wind. The particulars of the conductor are as follows : Size of conductor - 7/3.45 mm. Area of cross section - 64.5 mm² , weight 2 of conductor - 0.594 kgf/m. Modulus of elasticity - 12700 kgf/mm² , Coefficient of linear expansion - 1.7 × 10 /°C. Assume 1 m³ of ice to weight 913.5 kgf.

AU : May-14, Marks 16

Solution :

Review Question

1. Derive an expression for the tension and sag at erection in a overhead transmission line.