The Line Integral

The Line Integral

• Consider that the charge is moved from initial position B to the final position A, against the electric field   then the work done is given by,

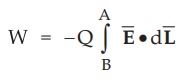
• This is called the line integral, where  gives the component of  along the direction .

• Mathematical procedure involved in such a line integral, is,

 1. Choose any arbitrary path B to A.

2. Break up the path into number of very small segments, which are called differential lengths.

3. Find the component of    along each segments.

4. Adding all such components and multiplying by charge, the required work done can be obtained.

• Thus line integral is basically a summation and accurate result is obtained when the number of segments becomes infinite.

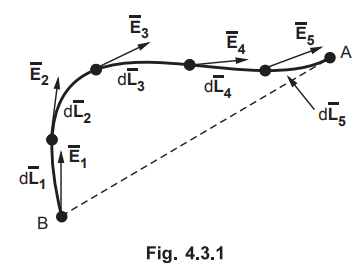
• Let us see an important property of this line integral. Consider an uniform electric field   . The charge is moved from B to A along the path shown in the Fig. 4.3.1.

• The path B to A is divided into number of small segments.

• The various distance vectors along the segments choosen are  while the electric field in these directions is 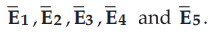 Hence the line integral from B to A can be expressed as the summation of dot products.

p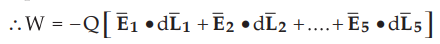

• But the electric field is uniform and is equal in all directions.

p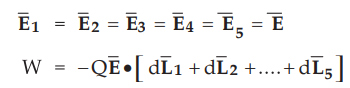

• Now 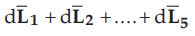 is the vector addition. So according to method of polygon the sum of all such vectors is the vector joining initial point to final point when all vectors are arranged one after the other in respective directions. This is shown in the Fig. 4.3.2. Hence the sum of all such vectors is the vector  joining initial point to final point.

p

• Thus it can be seen that vector sum of small segments choosen along any path, a curve or a straight line remains same as  and it depends on the initial and final point only.

Key Point : Hence the work done depends on Q,    and  and does not depend on the path joining B to A. This is true for nonuniform electric field    as well.

p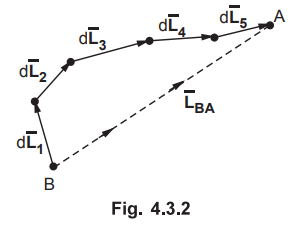

• Thus, the work done in moving a charge from one location B to another A, in a static, uniform or nonuniform electric field  is independent of the path selected. The line integral of  is determined completely by the endpoints B and A of the path and not the actual path selected.

Key Point : This is called conservative property of electric field  and field  is said to be conservative.

• While solving the problems, it is necessary to select  according to the conditions and co-ordinate system selected. The expressions for in three co-ordinate systems are given here again for the convenience of the readers.

1. Important Comments About Work Done

• The work done in moving a point charge in an electric field    from position B to A is given by,

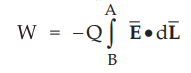
1. When the movement of the charge Q is against the direction of   , then the work done is positive, which indicates external source has done the work.

2. When the movement of the charge Q is in the direction of   , then the work done is negative, which indicates field itself has done the work, no external source is required.

3. The work done is independent of the path selected from B to A but it depends on end points B and A.

4. When the path selected is such that it is always perpendicular to    i.e. the force on the charge is always exerted at right angles to the direction in which charge is moving, then the work done is zero. This indicates e, the angle between    and  is 90°. Due to the dot product, the line integral is zero when θ = 90°.

5. If the path selected is such that it is forming a closed contour i.e. starting point is same as the terminating point then the work done is zero.

Ex. 4.3.1 Show that the vector field Ā is conservative if Ā possesses one of the following two properties.

1) The line integral of the tangential component of Ā along a path extending from a

point P to a point Q is independent of the path.

2) The line integral of the tangential component of Ā around any closed path is zero.

Sol. : Consider an uniform electric field Ā and the charge is moving from P and Q as shown in the Fig. 4.3.3. 

The path P to Q is divided into number of segments. The various distance vectors choosen are 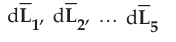 along the small segments while electric field in tangential directions is .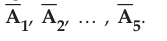

The line integral of the tangential component of Ā along the path can be expressed as the summation of the dot product of  and tangential component of Ā.

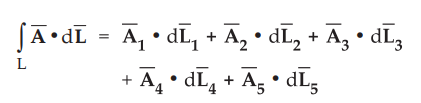
But the electric field is uniform and is equal in all the directions hence

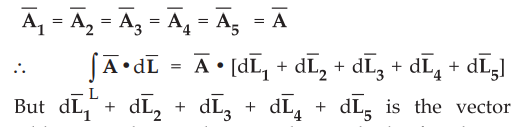
 addition and according to the method of polygon their sum is the vector joining initial point to the final point as shown in the Fig. 4.3.4.

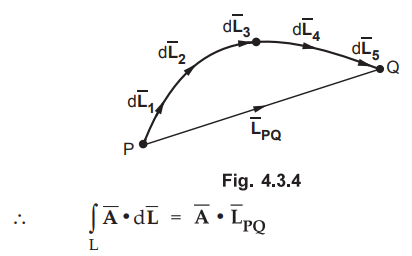
 The vector  depends only on the initial point P and final point Q irrespective of path selected joining P and Q.

Thus the line integral of the tangential component of Ā along a path extending from a point P to a point Q is independent of the path selected.

And if the path is closed then the starting and terminating point becomes same and the line integral is zero.

Such a vector Ā is called conservative in nature.

Ex. 4.3.2 Calculate the work done in moving a 4 C charge from B (1, 0, 0) to A (0,2, 0) along a straight path in the field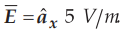 

Sol. :

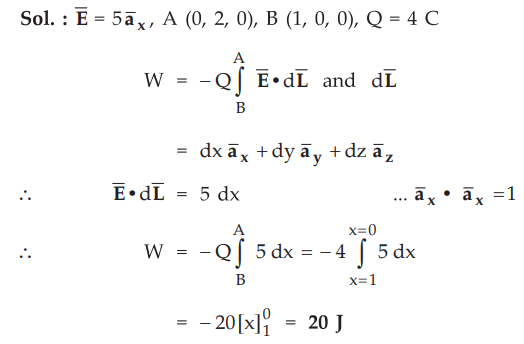
Ex. 4.3.3 A non uniform field 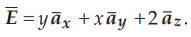 Determine the work expended in carrying 2C from B(l, 0, 1) to A(0.8, 0.6, 1) along the shorter arc of the circle x² + y² = 1 z = 1 Find the work required to carry same charge from B to A through straight line joining B to A in the same field.

Sol. :

Case 2 : To obtain equations of the straight line, any two of the following three equations of planes passing through the line are sufficient.

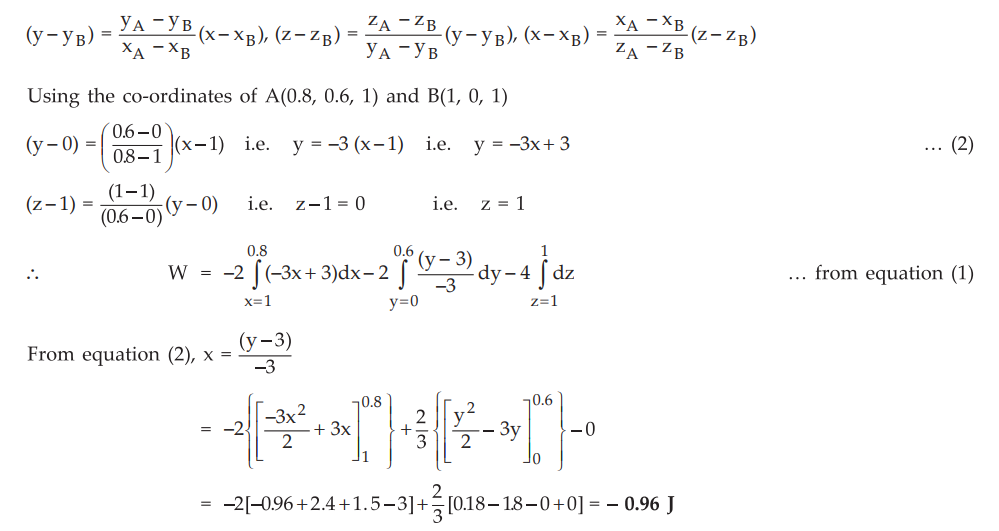
Ex. 4.3.4 Consider an infinite line charge with density ρ_L C/m, along z-axis. Obtain the work done if a point charge Q is moved from r = a to r = b along a radial path.

Sol. : The line charge and the path of the movement of the point charge Q is shown in the Fig. 4.3.5.

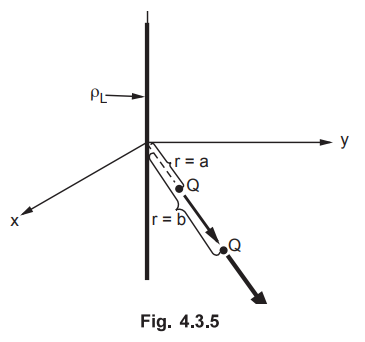
The movement of the point charge Q is along   direction and hence  has no component in 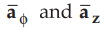 direction.

As b > a, In (b/a) is positive and work done is negative. This indicates that the field is doing the work and external source is receiving energy.

Ex. 4.3.5 Calculate the line integral of the vector field 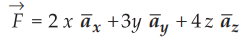 along the following two paths

joining the origin to the point P(l, 1, 1) i)

Along a straight line joining the origin to P.

ii) Along a path parameterized by x = t, y = t², z = t³.

From the result of this problem, can you conclude that the force is conservative ? If so, determine a potential function for this vector field.

AU : Dec.-19, Marks 13

Sol. :

As the line integral values are equal for any path selected, the force is conservative.

To find potential function for  means to find a scalar valued function f(x, y, z) such that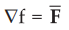 

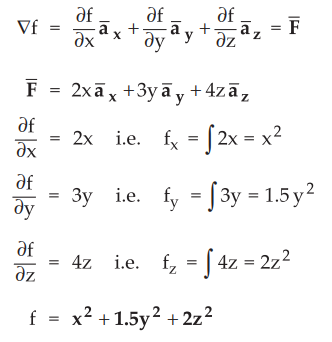
Examples for Practice

Ex. 4.3.6 Determine the work done in carrying a charge of - 5 C from (2, 1, -1) to (4, 2, -1) in the field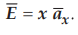 

[Ans.: 30 J]

Ex. 4.3.7 An electrostatic field is given by,

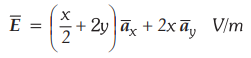
Find the work done in mouing a point charge of 20 LIC from (4, 2, 0) to (0, 0, 0) along a straight line path.

[Ans.: + 400 µJ]

Ex. 4.3.8 Find the work done in mouing a charge of + 2 C from (2, 0,0) m to (0, 2, 0) m along the straight line path joining two points, if the electric field is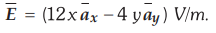 

[Ans.: + 64 J]

Ex. 4.3.9 Determine work done in carrying a charge of -2C from (2,1, - 1) to (8, 2,-1) in the electric field

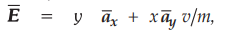, (in Cartesian co-ordinates) considering the path along the parabola x = 2y².   

[Ans.: 28 J]

Review Question

1. Show that the line integral 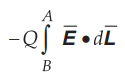 is not dependent on the path selected between B to A but only depends on the end points B and A.

Potential Difference