Thevenin's Theorem

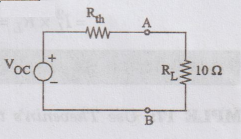
THEVENIN'S THEOREM

This theorem is useful when it is necessary to find the current in only one branch of a network.

Statement

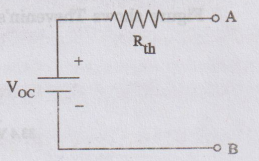
Across a pair of terminals AB, any linear network can be replaced by an equivalent circuit composed of a voltage source V_oc in series with a resistance R_th. The voltage

V_OC is the voltage across the open circuited terminals AB and R_th is the equivalent resistance of the network as seen from terminals AB with all independent sources are replaced by their internal resistances.

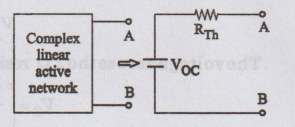
where,

V_OC → Open circuit voltage across terminals AB

R_th → Thevenin's resistance across teminals AB

Explanation

To calculate V_OC

III que

Remove the load resistor and then measure the voltage appearing across the load terminals which gives the open circuit voltage Voc

To calculate R_th

1. Remove the load resistor.

2. Short circuit the voltage source (or replace the voltage source by its internal resistance).

3. Open circuit the current source (or replace the current source by its internal resistance).

4. Then, measure the resistance at load terminal which is the Thevenin's resistance (Rth).

Proof

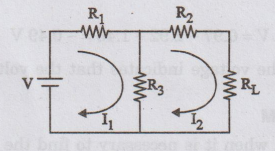
Consider the given network consisting of a voltage source V and resistors R₁, R₂, R₃ and R_L.

To calculate I_L

Method 1

By Mesh Analysis

Method II

By Thevenin's Theorem,

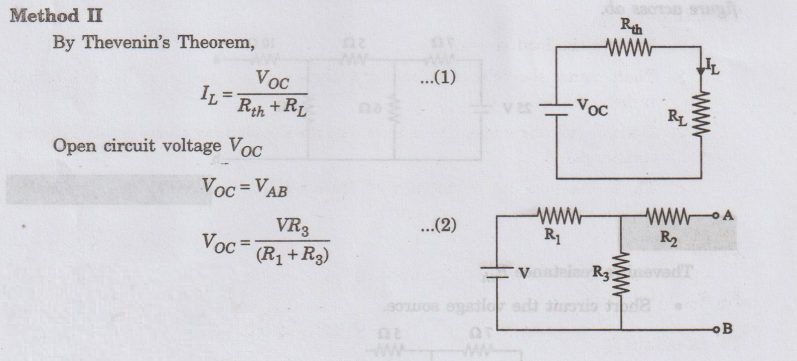
Calculate Rth

Remove the load resistor (R_L).

Short circuit the voltage source (V).

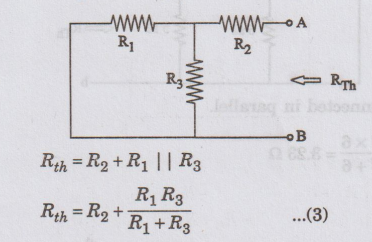
Substituting equations (2) and (3) in (1)

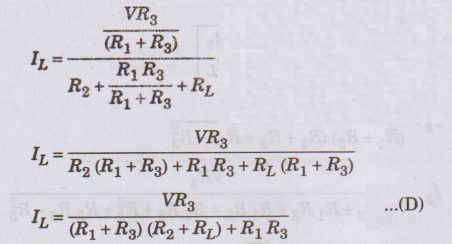
Equations (C) and (D) are the same. Hence, the Thevenin's theorem is proved.

 

EXAMPLE 11: Find the Thevenin's voltage and Thevenin's resistance for the circuit of figure across ab.

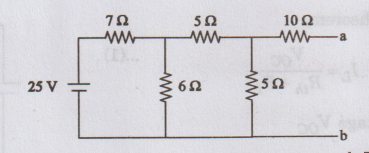
Solution :

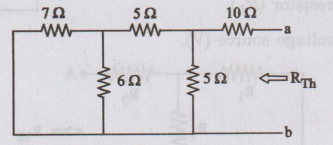
Thevenin's resistance R_th

• Short circuit the voltage source.

7 Ω and 6 Ω are connected in parallel.

7 × 6 / 7 + 6 = 3.23 Ω

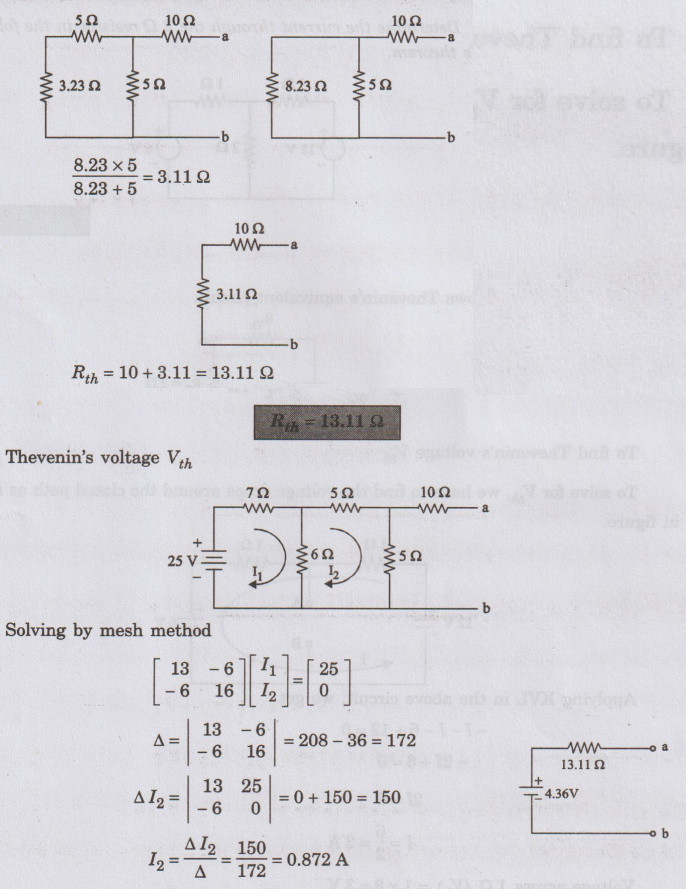
Voltage across ab = Voltage across 5 Ω resistor

= 5 × 0.872 = 4.36 V

V_OC = 4.36 V

 

EXAMPLE 12: Determine the current through the 2 2 resistor in the following network using Thevenin's theorem.

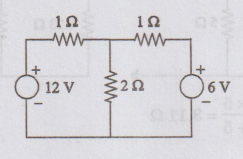
Solution :

Figure shows Thevenin's equivalent circuit.

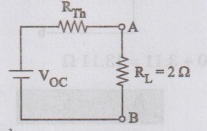
To find Thevenin's voltage V_th

To solve for V_th, we have to find the voltage drops around the closed path as shown in figure.

 

EXAMPLE 13: Determine Thevenin's equivalent across the terminals AB for the circuit shown in figure.

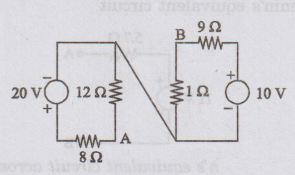
Solution:

The given circuit is redrawn as shown in figure.

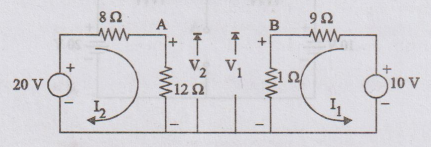
Voltage V_AB = V₂ + V₁

Applying KVL to loop 1

I₂ = 20 / 20 = 1 A

Voltage drop across 12 Ω resistor V₂

V₂ = 12 × 1 = 12 V

Apply KVL to loop 2

I₁ = 10 / 10 = 1A

Voltage across 1 Ω resistor V₁ =1 × 1= 1V

V_AB = V₂ + V₁ = 12 – 1 = 11V

 

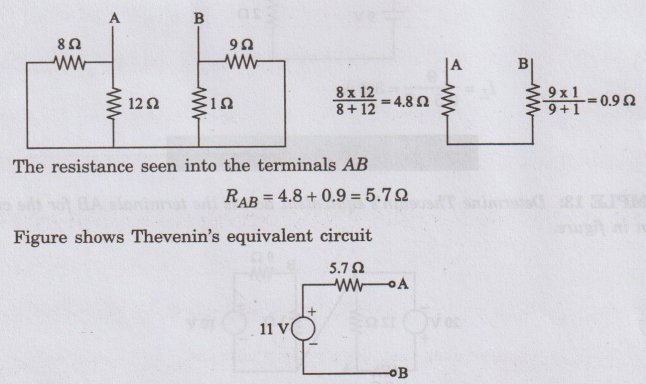
EXAMPLE 14: Find the Thevenin's equivalent circuit across the terminals A and B for the network shown in figure. (AU/EEE- Nov 2005)

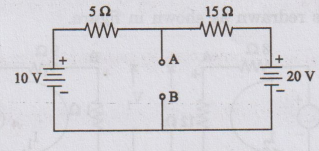
Solution:

The complete circuit can be replaced by a voltage source in series with a resistance as shown in figure.

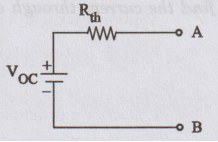
where V_OC is the voltage across terminals AB.

To solve for V_OC, we have to find the voltage drops around the closed path as shown in figure.

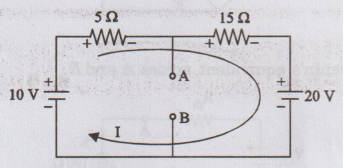
Applying KVL in the above circuit, we get

-5I – 15I - 20 + 10 = 0

-20I -10 = 0

- 20I = 10

I = - 10 / 20 = - 0.5 A

Voltage across 5 Ω = -0.5 × 5 = -2.5 V

Voltage across 15 Ω = 15 ×  -0.5 = -7.5 V

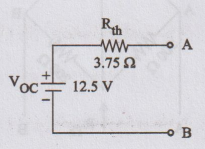
Thevenin's voltage V_OC = V_AB = 10 - V₅ = 10 + 2.5 = 12.5 V

To find R_th, the two voltage sources are short circuited.

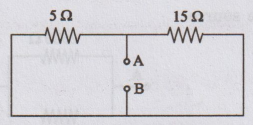
Here the 5 Ω and 15 Ω are connected in parallel.

R_th = 5 × 15 / 5 + 15 = 3.75 Ω

Figure shows Thevenin's equivalent circuit.

 

EXAMPLE 15: Determine the Thevenin's equivalent circuit of the network given. Also find the current through a 100 Ω galvanometer connected across AB.

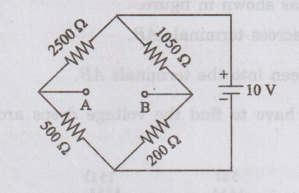
Solution:

Figure shows Thevenin's equivalent across A and B.

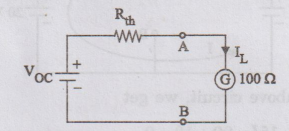
To calculate Thevenin's voltage (V_OC):

 

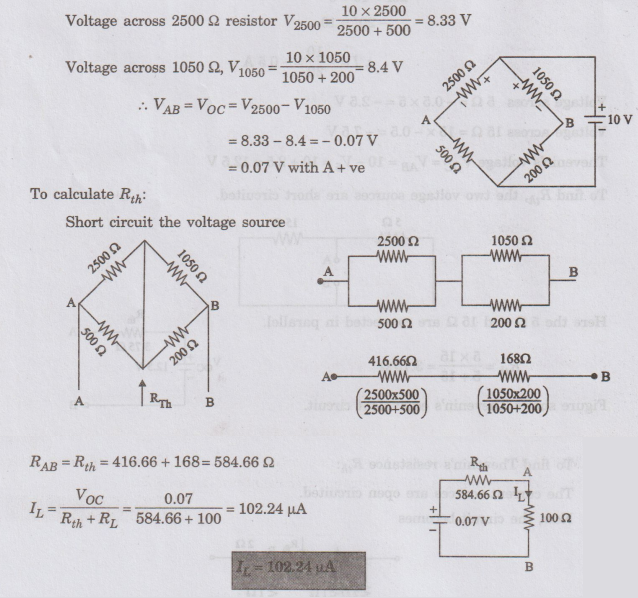
EXAMPLE 16: Determine the power loss in 10 Q resistor (use Thevenin's theorem). (AU, Coimbatore/EEE - May 2008)

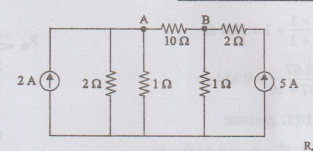
Solution :

Thevenin's equivalent circuit across the terminals AB is

To find Thevenin's voltage V_OC:

Remove the load resistor 10 Ω

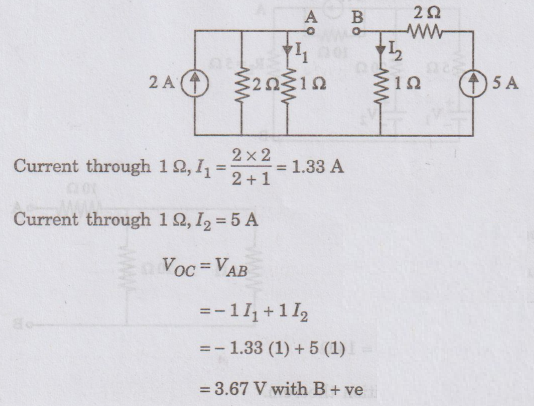
To find Thevenin's resistance R_th:

The current sources are open circuited.

Now, the circuit becomes

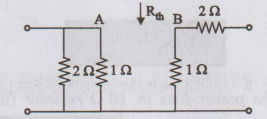
Here 2 Ω resistor connected at B is inactive.

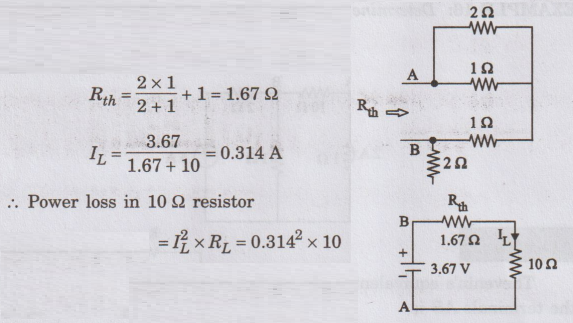
Power loss in 10 Ω resistor = 0.9859 W

 

EXAMPLE 17: Use Thevenin's theorem to find current through R_L in the network if V₁ = V₂=10 V.

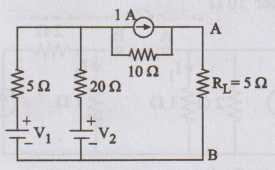
Solution:

To calculate R_th

•  Remove the load resistor RL

•  Short circuit the voltage source

•  Open circuit the current source.

R_th = 10 + 5 × 20 / 25 = 14 Ω

To calculate Voc, apply Superposition theorem.

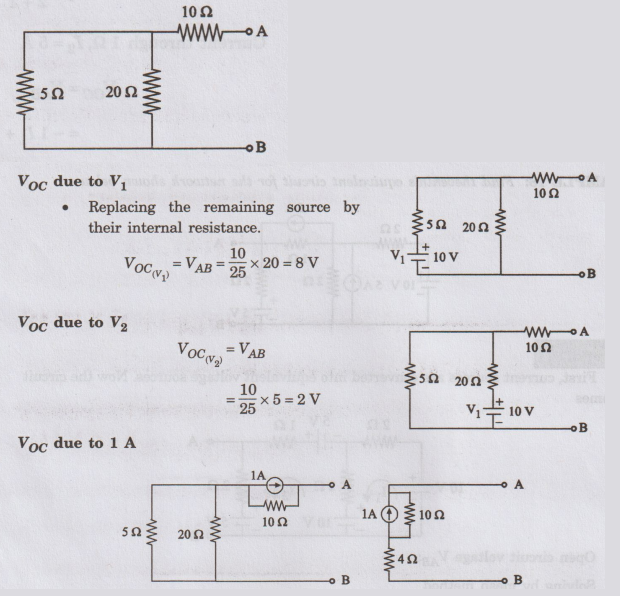
5 and 20 Ω are connected in parallel i.e., 5 × 20 / 5 + 20 = 4 Ω

V_OC(1A) = V_AB

= V_10Ω = 10 × 1 = 10 V

Since, there will be no current through 4 Ω.

V_OC for the given network

 

EXAMPLE 18: Find thevenin's equivalent circuit for the network shown below.

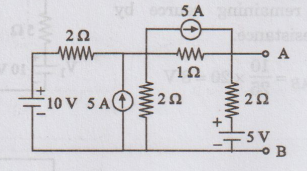
Solution :

First, current sources are converted into equivalent voltage sources. Now the circuit becomes

Thevenin's Resistance

1. Short circuit the voltage sources

2. Open circuit the current sources

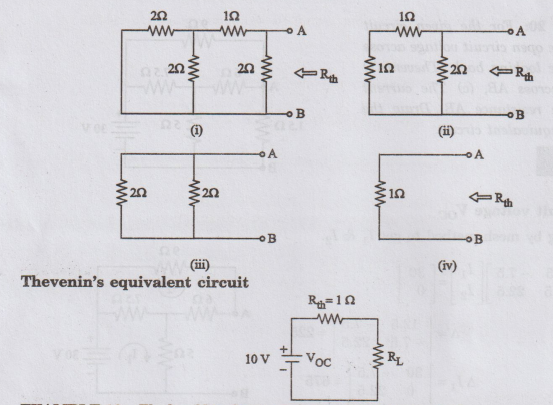
 EXAMPLE 19: The box N in figure contains energy sources and resistors. The open circuit voltage across the terminals a b is 5 volts. When the terminals a and b are shorted, the short-circuit current is 1 A. Determine the current that flows through a resistor of 5 when it is connected across ab.

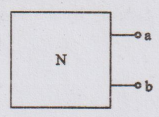
Solution:

Open circuit voltage across ab, V_OC = 5 V

Short circuit current through ab, I_SC = 1 A

Relationship between V_OC, I_SC and R_th R_th = V_OC / I_SC = 5/1 = 5 Ω

Thevenin's Equivalent Circuit

 

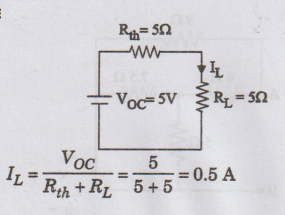
EXAMPLE 20: For the given circuit find (a) The open circuit voltage across AB, (b) The looking back (Thevenin's) resistance across AB, (c) The current through the resistance AB. Draw the Thevenin's equivalent circuit.

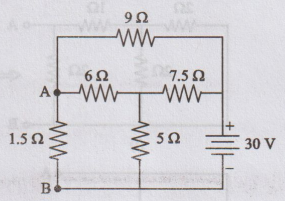
Solution:

Open circuit voltage V_OC

Solving by mesh method to get I₁ & I₂.

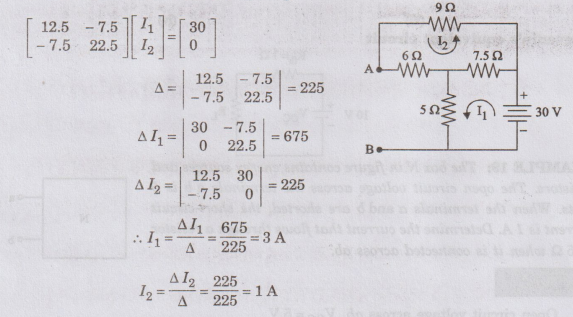
Voltage across AB = Voltage across 5 Ω resistor + Voltage across 6 Ω resistor

= (5 × 3) + (6 × 1)

V_OC = 15 + 6 = 21 V

Thevenin's Resistance

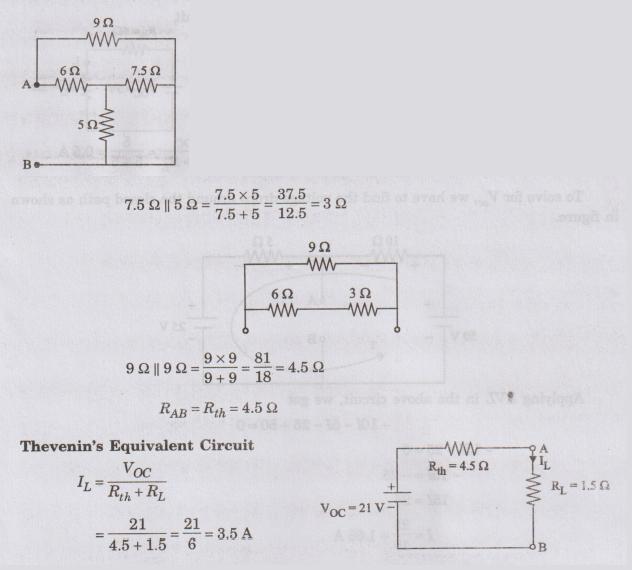
Current through 1.5 Ohm resistance is 3.5 A

 

EXAMPLE 21: Determine the Thevenin's equivalent circuit across 'AB' for the circuit shown in figure.

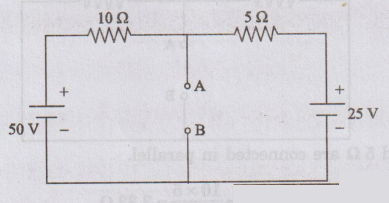
Solution:

The complete circuit can be replaced by a voltage source in series with resistance as shown in figure. where V_OC is the voltage across terminals AB.

R_th is the resistance between the terminals AB.

To solve for V_OC, we have to find the voltage drops around the closed path as shown in figure.

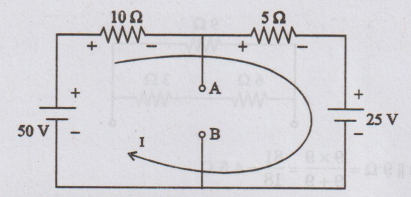
Applying KVL in the above circuit, we get

-10I – 5I - 25 + 50 = 0

- 15I = -25

15I = 25

I = 25 / 15 = 1.66 A

Voltage across 10 Ω = 1.66 × 10 = 16.6V

Thevenin's voltage V_OC = V_AB = 50 - 16.6 = 33.4 V

To find R_th, the two voltage sources are replaced with short circuit.

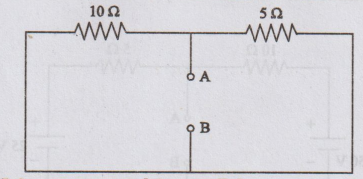
Here 10 Ω and 5 Ω are connected in parallel.

R_th = 10 × 5 / 10 + 5 = 3.33 Ω

Figure shows Thevenin's equivalent circuit.

 

EXAMPLE 22: Using Thevenin's theorem find the current through 5 resistance.

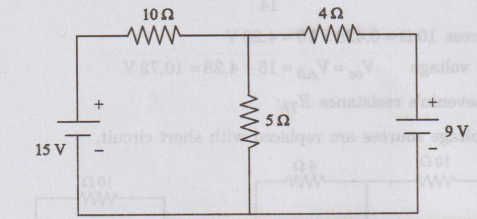
Solution:

Figure shows Thevenin's equivalent circuit.

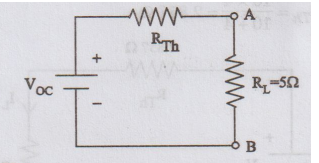
Thevenin's voltage Voc

To solve for V_OC, we have to find the voltage drops around the closed path as shown in figure.

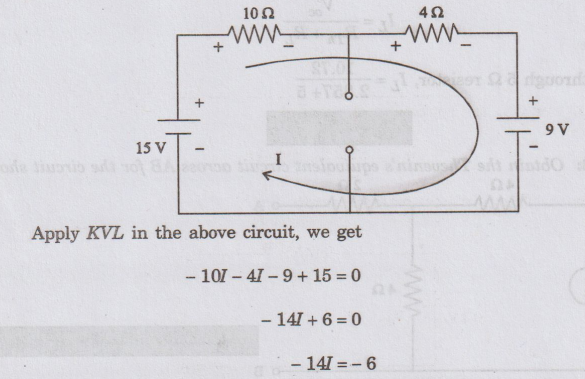
I = 6 / 14 = 0.428 A

Voltage across 10 Ω = 0.428 × 10 = 4.28 V

Thevenin's voltage V_oc = V_AB = 15 - 4.28 = 10.72 V

To find Thevenin's resistance R_Th

The two voltage sources are replaced with short circuit.

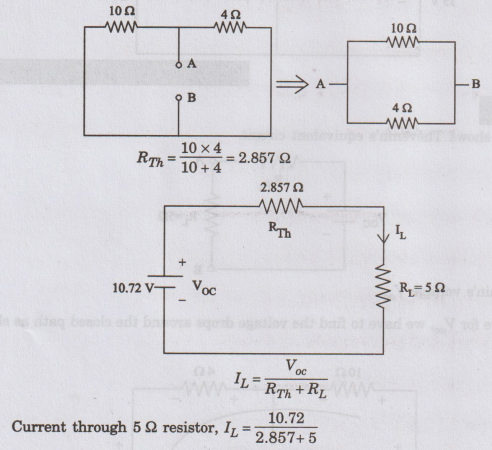
I_L =1.364 A

 

EXAMPLE 23: Obtain the Thevenin's equivalent circuit across AB for the circuit shown in figure.

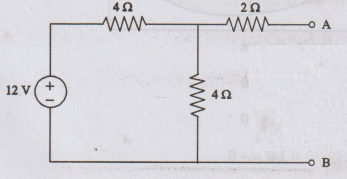
Solution:

Thevenin's resistance R_Th

Short circuit the voltage source.

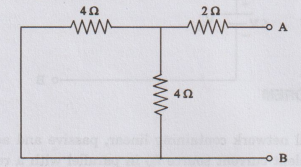
4 Ω and 4 Ω are connected in parallel.

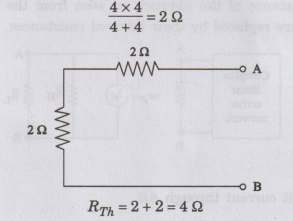
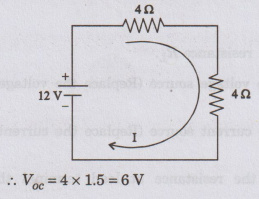
Thevenin's voltage (V_OC):

I = 12 / 4 + 4 = 12 / 8 = 1.5 A

Voltage across AB = V_OC = voltage across 4 Ω

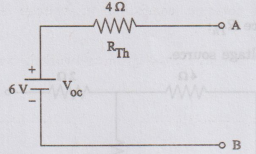
Now, the Thevenin's equivalent circuit is