Electric Circuit Analysis: Unit I: b. Basic circuits analysis
To find RMS or effective values of some important waveforms
RMS value of half wave rectified waveform
TO FIND RMS OR EFFECTIVE VALUES OF SOME IMPORTANT WAVEFORMS
RMS
value of half wave rectified waveform :
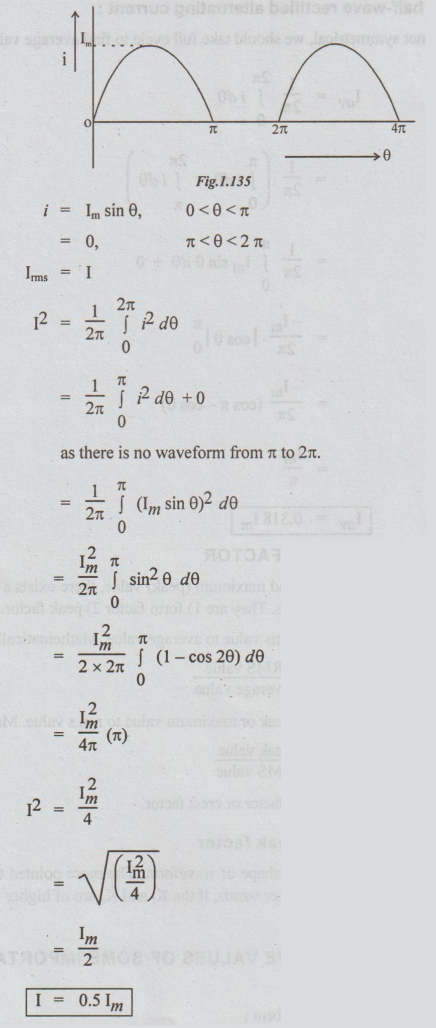
2.
Average value of half-wave rectified alternating current :
As
the waveform is not symmetrical, we should take full cycle to find average
value.
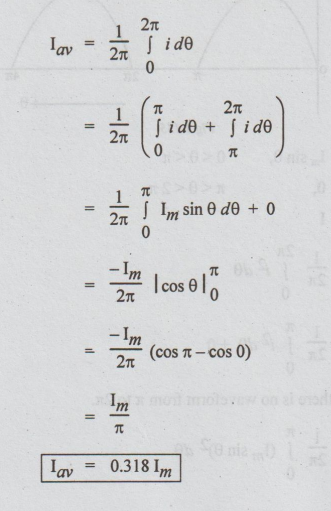
For
a half wave rectified wave form
RMS
value = 0.5 × maximum value
Average
value = 0.318 × maximum value
Form
factor of a half wave rectified alternating current
Kf
= RMS value / Average value
=
0.5 × maximum value / 0.318 × maximum value
Kf
= 1.57
3.
RMS value and average value of a full wave rectified sinusoidal wave form
For
a full wave rectified sine wave form,
4.
To find RMS value average value, Kf and Ka for a
saw-tooth wave form
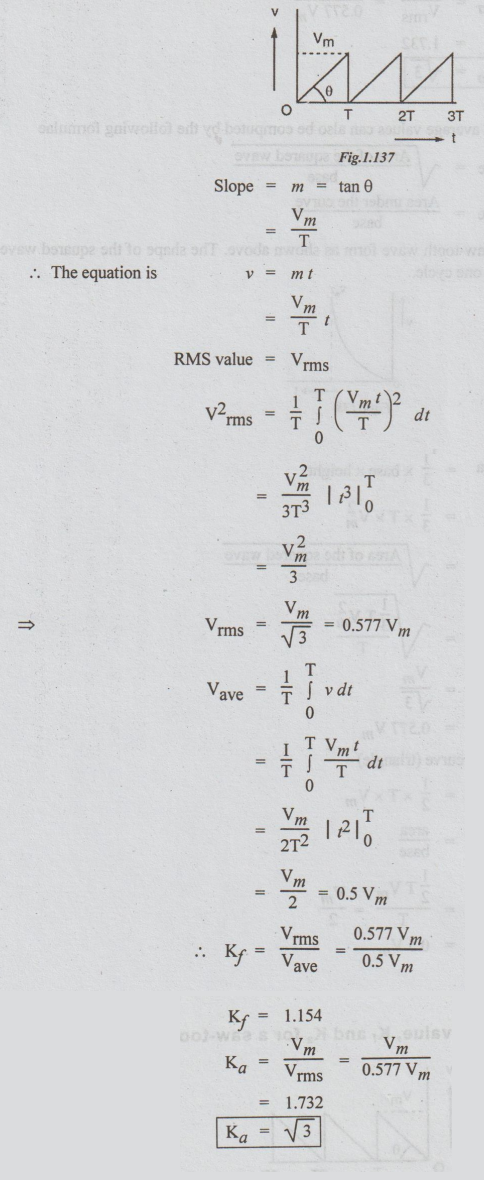
Note
1.
As mentioned earlier, RMS and average values can also be computed by the
following formulae
RMS
value = √Area of the squared wave / base
Average
value = Area under the curve / base
As
an example let us take the saw-tooth wave form as shown above. The shape of the
squared wave form is as shown below. Take only one cycle.
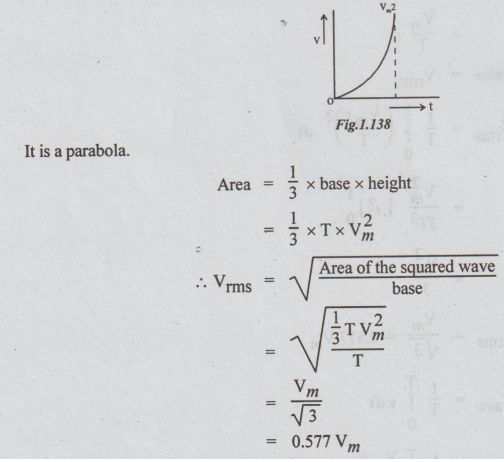
Area
of the wave form under the curve (triangle)
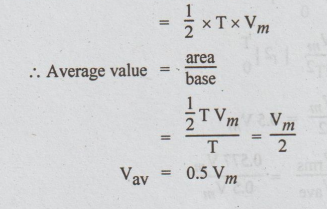
Note
2:
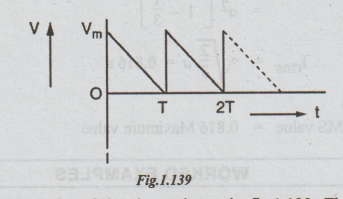
The
saw-tooth wave form may be of the shape shown in fig.1.139. The equation is
obtained by intercept formula. Here also
Vms
= 0.577 Vm
Vav
= 0.5 Vm
5.
To find the RMS value of a semi circular current wave which has a maximum value
of 'a'
Solution:
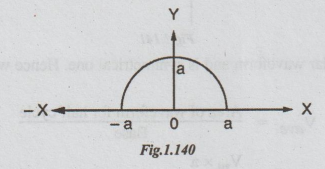
The
equation of the semi circular wave is
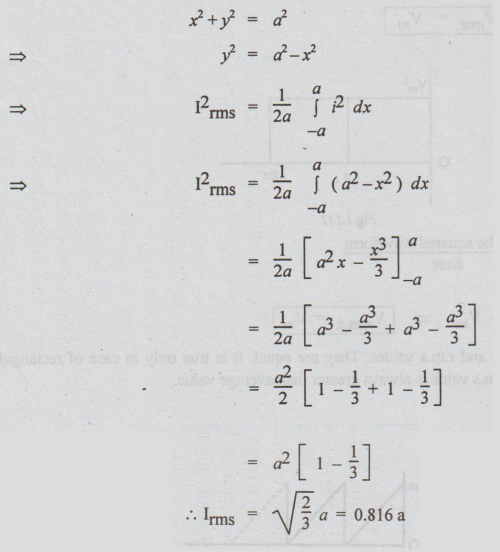
For
a circular wave,
RMS
value = 0.816 Maximum value
Electric Circuit Analysis: Unit I: b. Basic circuits analysis : Tag: : - To find RMS or effective values of some important waveforms
Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation