Torque Equation

Torque Equation

The torque produced in the induction motor depends on the following factors.

1. The part of rotating magnetic field which reacts with rotor and is responsible to produce induced e.m.f. in rotor.

2. The magnitude of rotor current in running condition.

3. The power factor of the rotor circuit in running condition.

Mathematically the relationship can be expressed as,

T ∝  ϕ I_2r cos ϕ_2r   ...(5.9.1)

where          ϕ = Flux responsible to produce induced e.m.f.

I_2r - Rotor running current

cos ϕ_2r = Running p.f. of rotor

The flux ϕ produced by stator is proportional to E₁i.e. stator voltage.

ϕ ∝ E₁         ... (5.9.2)

While E₁ and E₂ are related to each other through ratio of stator turns to rotor turns i. e. K.

E₂ / E₁ = K  ... (5.9.3)

Using equation (5.9.3) in equation (5.9.2) we can write,

E₂  ∝ ϕ ... (5.9.4)

Thus in equation (5.9.1), ϕ can be replaced by E₂.

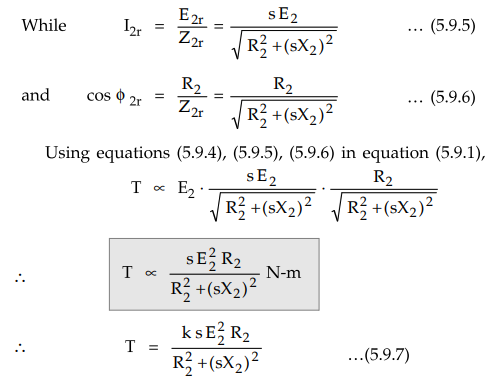
where K = Constant of proportionality

The constant k is proved to be 3/2πn_s for the three phase induction motor.

k = 3/2πn_s

Key Point n_S = Synchronous speed in r.p.s. = N_S/60

Using equation (5.9.8) in equation (5.9.7) we get the torque equation as,

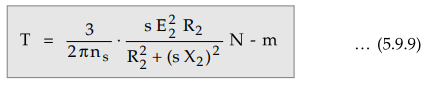
So torque developed at any load condition can be obtained if slip at that load is known and all standstill rotor parameters are known.

1. Starting Torque

Starting torque is nothing but the torque produced by an induction motor at start. At start, N = 0 and slip s = 1. So putting s = 1 in the torque equation we can write expression for the starting torque T_st as,

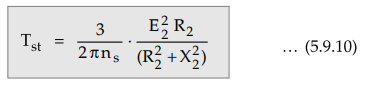
Key Point From the equation (5.9.10), it is clear that by changing R2 the starting torque Tst can be controlled.

The change in R₂ at start is possible in case of slip ring induction motor only. This is the principle used in case of slip induction motor to control the starting torque T_st.

Example 5.9.1 A 3 phase, 400 V, 50 Hz, 4 pole induction motor has star connected stator winding. The rotor resistance and reactance are 0.1 Q and 1 Q respectively. The full load speed is 1440 r.p.m. Calculate the torque developed on full load by the motor. Assume stator to rotor ratio as 2 : 1. 

Solution : The given values are,

Example for Practice

Example 5.9.2 A 4 pole, 50 Hz, 3-ϕ, IM has a rotor resistance of 4.5 Q / phase and standstill reactance of 8.5 Ω / phase. With no external resistance in the rotor circuit, the starting torque of the motor is 85 N-m.

i) What is the rotor voltage at standstill ?

ii) What would be the starting torque if 3 Ω resitance were added in each rotor phase ?

iii) Neglecting stator voltage drop, what would be the induced rotor voltage and the torque at a slip of 0.03 ?

[Ans.: i) 302.46 V/ph, ii) 101.975 Nm, iii) 9.0738 V, T = 11.61 Nm]

Review Question

1. Derive the torque equation for a three phase induction motor. AU : May-04, 11, Marks 8, May-16, Dec.-17, Marks 4