Transformation of random variables

TRANSFORMATION OF RANDOM VARIABLES

 

1. Two functions of two random variables

If (X, Y) is a two dimensional random variable with joint p.d.f. fxy (x, y) and if Z = g(X, Y) and W = h (X, Y) are two other random variables then the joint p.d.f of (Z, W) is given by,

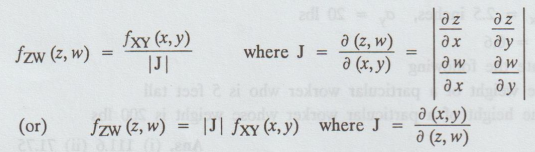
Note: This result holds good, only if the equation Z = g (X, Y) and w = h (X, Y) when solved, give unique values of x and y in terms of z and w.

 

2. One function of two random variables

If a random variable Z is defined as Z = g (X, Y), where X and Y are given random variables with joint p.d.f f(x, y). To find the pdf of Z, we 0= introduce a second Random variable W = h(X, Y) and obtain the joint p.d.f of (Z, W), by using the previous result. Let it be fzw (z, w). The required p.d.f of Z is then obtained as the marginal p.d.f is fz (2) is obtained by simply integrating fzw (Z, W) w.r. to w.

 

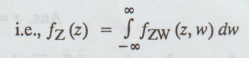
Example 2.4.1

Let (X, Y) be a two-dimensional non-negative continuous random variable having the joint density.

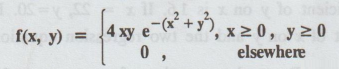
Find the density function of U = √X² + Y²

[A.U A/M 2005] [A.U Tvli M/J 2010. Tvli A/M 2011] [A.U M/J 2016 R13 (RP)]

Solution:

The density function of U is

 

Example 2.4.2

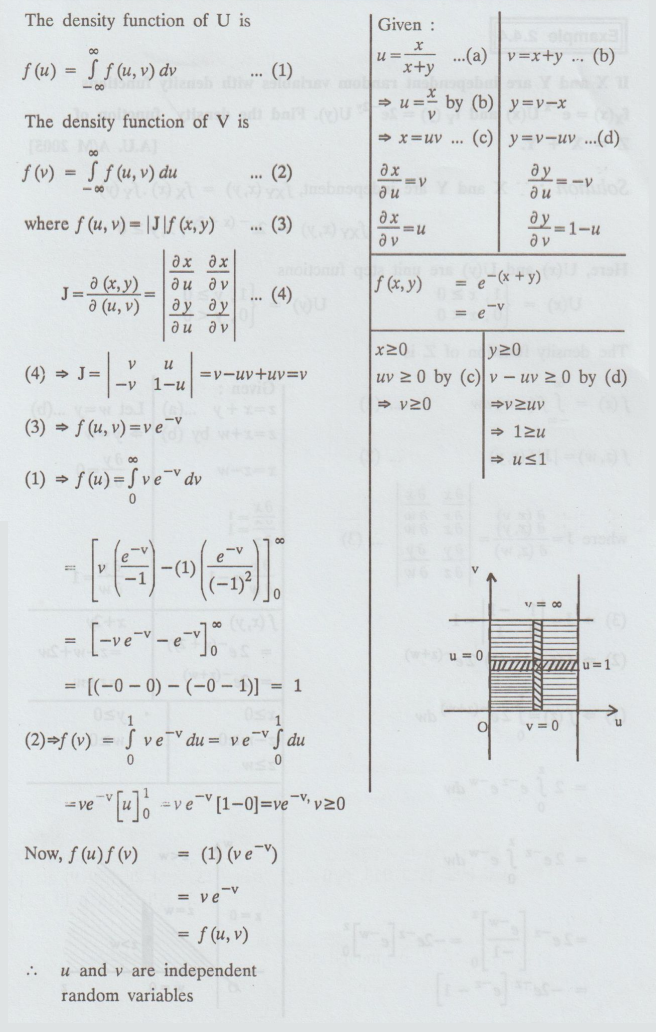
If U = X + Y and V = X - Y, how are the joint p.d.f's of (X, Y) and (U, V) related?

Solution :

 

Example 2.4.3

If X and Y are independent random variables with p.d.f e^-x, x = 0; e^-y y ≥ 0 respectively. Find the density function of U = X / X + Y. and V = X + Y. Are U & V independent ?

 [A.U. N/D 2006] [A.U Trichy M/J 2009, A.U N/D 2009, N/D 2011, N/D 2013] [A.U N/D 2015 R13, N/D 2017 (RP) R13, A/M 2017 (RP) R13] [A.U N/D 2018 R-17 PS]

Solution:

Since, X and Y are indepdendent,

f(x,y) = e^-x.e ^–y = e ^{̄(x + y)}, x, y ≥ 0

The density function of U is

 

Example 2.4.4

If X and Y are independent random variables with density functions fx(x) = e^-x U(x) and fy (y) = 2e^-2y U(y). Find the density function of Z = X + Y.  [A.U. A/M 2005]

Solution :

X and Y are independent, f_XY (x, y) = f_X (x) .f_Y (y)

f_XY (x, y) = 2e^{-(x + 2y)} , x,y, ≥ 0

Here, U(x) and U(y) are unit step functions

 

Example 2.4.5

If X and Y are independent random variables with density function fx(x) = 1, in 1 ≤ x ≤ 2 and fy (y) = 2, in 2 ≤ y ≤ 4, find the density function  of Z = XY. [A.U A/M 2011]

Solution

X and Y are independent, f_XY (x, y) = f_X (x) .f_Y (y)

Example 2.4.6

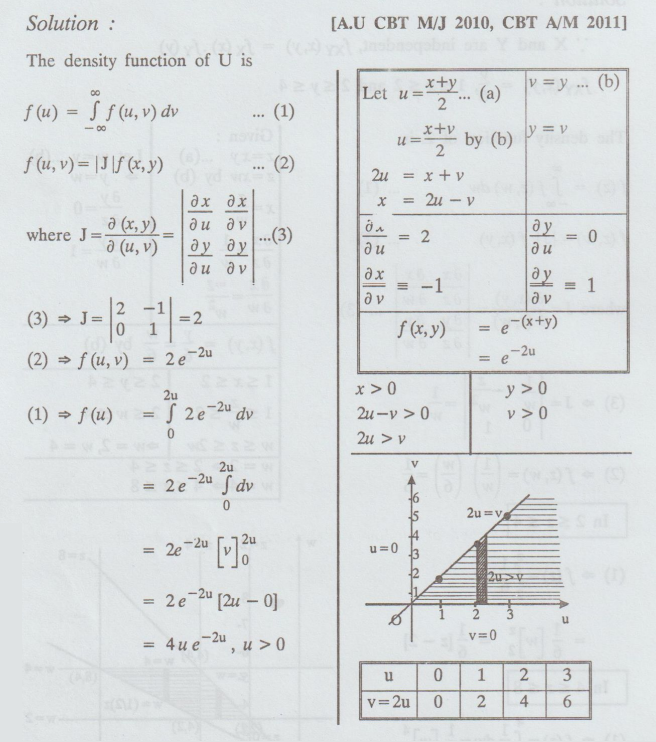
The joint p.d.f. of X and Y is given by f (x, y) = e –(x+y), x > 0, y > 0,

find the probability density function of U = X + Y / 2

 [AU A/M 2003] [A.U. N/D 2006] [AU N/D 2009]

[A.U CBT M/J 2010, CBT A/M 2011]

Solution :

The density function of U is

 

Example 2.4.7

If X and Y are independent random variables each following N (0, 2), find the probability density function of Z = 2X + 3Y.

[AU A/M. 2003]

Solution :

Given: X follows N(0, 2) and

Y follows N(0, 2)

Z = 2x + 3y follows N (2 × 0 + 3 × 0, √2² × 2² + 3² × 2²)

i.e., Z = 2x + 3Y follows N (0, √52)

Z is a normal random variable with mean 0 and standard deviation √52

So, the p.d.f of Z is

 

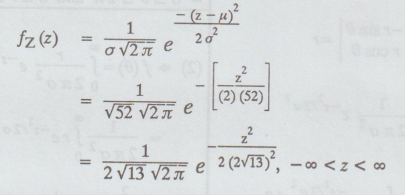
Example 2.4.8

If X and Y are independent random variables each normally distributed with mean zero and variance of σ² find the density functions of R = √X² + Y² and θ = tan -1(Y/X)

[A.U. Dec.03, N/D 2013] [A.U N/D 2017 R-13]

Solution:

Since X and Y are independent random variables normally distributed with mean zero and variance σ², the joint pdf of X and Y is given by

 

Example 2.4.9

The random variables X and Y are statistically independent having a gamma distribution with parameters (m, 1/2) and (n, 1/2) respectively. Derive the probability density function of a random variable U = X / (X + Y)

 [AU N/D 2007, A.U N/D 2008]

Solution :

Since X and Y are independent f (x, y) = f(x) ƒ (y)

 

Example 2.4.10

If X and Y are independent exponential distributions with parameter 1, then find the p.d.f of U = X - Y.

 [A.U. Model, M/J 2007, M/J 2013]

[A.U N/D 2015 R13 RP, N/D 2016 R13 PQT]

[A.U N/D 2015 R-8, A/M 2017 R-08]

[A.U N/D 2018 R-13 RP]

Solution:

The p.d.f of X and Y are

fx(x) = e^-x, x > 0 and f_Y(y) = e^-y, y > 0

Since X and Y are independent, the joint p.d.f is

f_XY (x,y) = f_X (x) f_Y (y)

= e^-x e^-y     x,y >0

= e^{− (x + y)},   x, y > 0

 

Example 2.4.11

If X and Y are independent random variables having density functions f(x)

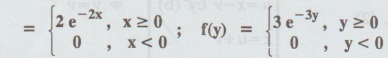 respectively, find the density find the functions of Z = X - Y.

 [A.U A/M 2011]

Solution:

 

Example 2.4.12

If the p.d.f of a two dimensional R.V (X, Y) is given by f(x, y) = x+y, 0 ≤ (x, y) ≤ 1. Find the p.d.f of U= XY.

[A.U Model] [A.U N/D 2006] [A.U Trichy A/M 2010] [A.U Tvli N/D 2010, Trichy M/J 2011] [A.U M/J 2012] [A.U A/M 2015 (RP) R13, N/D 2017(RP) R08] W6 [A.U A/M 2018 R13] [A.U N/D 2018 R-13 PQT]

Solution :

The density function of u is

 

Example 2.14.13

If Z = g(X, Y) and W= h (X, Y), how are the joint p.d.f's of (X, Y) and (Z, W) related ?

Solution :

 

Example 2.4.14

If Z = 2X + 3Y and W = Y, how are the joint p.d.f's of (X, Y) and (Z, W) related?

Solution :