Transformation of Vectors

Transformation of Vectors

AU : May-03, 11, 13, 14,19, Dec.-lO, 12, 13, 14, 16,18

• Getting familiar with the dot product and cross product, it is possible now to transform the vectors from one co-ordinate system to other co-ordinate system.

 

1. Transformation of Vectors from Cartesian to Cylindrical

• Consider a vector   in cartesian co-ordinate system as,

 ...(1.13.1)

• While the same vector 7 in cylindrical co-ordinate system can be represented as,

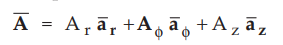  ...(1.13.2)

• From the dot product it is known that the component of vector in the direction of any unit vector is its dot product with that unit vector. 

Hence the component of   in the direction  is the dot product of   with . This component is nothing but A_r.

  

• The magnitudes of all unit vectors is unity hence it is necessary to find angle between the unit vectors to obtain the various dot products.

• The Fig. 1.13.1 (a) shows three dimensional view of various unit vectors.

• Consider a xy plane in which the angles between the unit vectors are shown, as in the Fig. 1.13.1 (b).

• The result of dot product are summarized in the tabular form as,

• The results of transformations can be expressed in the matrix form as,

2. Transformation of vectors from Cylindrical to Cartesian

• Now it is necessary to find the transformation from cylindrical to cartesian hence assume   is known in cylindrical system. Thus component of   in direction is given by,

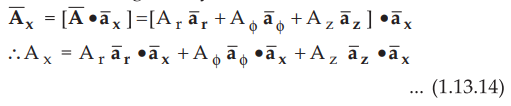
• As dot product is commutative  = cos ϕ and so on. Hence referring Table 1.13.1 we can write the results directly as,

A_x = A_r cos ϕ - A_ϕ sin ϕ  ...(1.13.15)

A_y = A_r sin ϕ + A_ϕ cos ϕ ...(1.13.16)

A_z = A_z        ... (1-13-17)

• The result can be summarized in the matrix form as,

 

 

3. Transformation of Vectors from Cartesian to Spherical

• Let the vector   expressed in the cartesian system as,

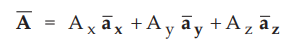
• It is required to transform it into spherical system. The component of direction is given by,

Note : Though the radius representation r used in cylindrical and spherical systems is same, the directions   in both the systems are different. Infact many times r is represented as p in cylindrical system. But ρ is used to represent other quantity in this book hence r is used in cylindrical system. Hence 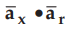 will be different when  is of spherical system than the   of cylindrical system and so on.

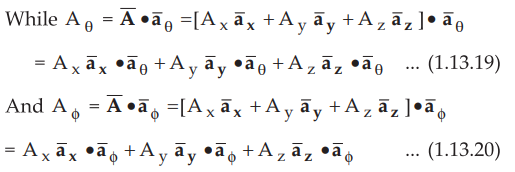
• The dot products can be obtained by first taking the projection of spherical unit vector on the xy plane and then taking the projection onto the desired axis. Thus for 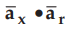 project   on the xy plane which is sin e and then project on the x axis which is sin θ cos ϕ.

• In the similar fashion the other dot products can be obtained. The results of the dot products are summarized in the Table 1.13.2.

• Using the results of Table 1.13.2, the results of vector transformation from cartesian to spherical can be summarized in the matrix form as,

4. Transformation of Vectors from Spherical to Cartesian

• To find the reverse transformation, assume that the   is known in spherical system as,

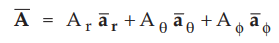
• Hence component of respectively.

• Thus we get the results as,

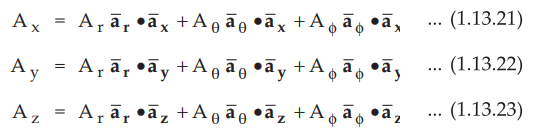
• Using the Table 1.13.2, the results can be expressed  in the matrix form as,

 

5. Distances in all Co-ordinate Systems

• Consider two points A and B with the position vectors as,

• then the distance d between the two points in all the three co-ordinate systems are given by,

• These results may be used directly in electromagnetics wherever required.

 

Ex. 1.13.2 Obtain the spherical co-ordinates of 10  at the point P (x = -3,y = 2, z = 4).

Sol. : Given vector is in cartesian system say 

Then   sin θ cos ϕ    ... Refer Table 1.13.2

At point P, x = - 3, y = 2, z = 4

Using the relationship between cartesian and spherical,

 x = r sin θ cos ϕ y = r sin θ sin ϕ z = r cos θ

          ϕ = tan^-1 y/x = tan^-1 2/-3  = - 33.69°

But x is negative and y is positive hence ϕ must be between +90° and +180°. So add 180^o to the ϕ to get correct ϕ.

          ϕ = - 33.69^o + 180° = + 146.31^o i.e. cos ϕ = - 0.832 and sin ϕ = 0.5547

And   

 

6. Transformation of Vectors from Spherical to Cylindrical

• Let the vector   is known in the spherical co-ordinates.

• The components of   in cylindrical system are given by,

 

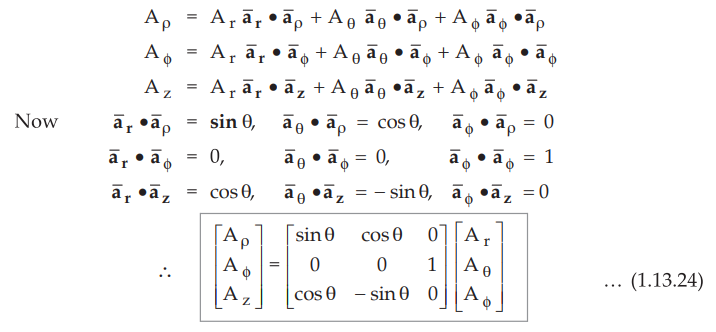
7. Transformation of Vectors from Cylindrical to Spherical

• Let the vector  is known in the cylindrical co-ordinates.

• The components of  in the spherical system are given by,

Key point : To avoid the confusion between , in cylindrical and spherical in the cylindrical system , is used.

• Using equations (1.13.24) and (1.13.25), any vector can be converted from cylindrical to spherical or spherical to cylindrical system.

 

Ex. 1.13.3 Express vector in cartesian and cylindrical systems. Given

Then find  at ( -3,4,0) and ( 5, π/2,-2) AU : Dec.-13,18,May-19,Marks 16

Sol. :

Ex. 1.13.5 Given point P (-2, 6, 3) and, express P and   in cylindrical co-ordinates. AU : Dec.-12, Marks 8

Sol. : Refer example 1.13.4 for P in cylindrical system.

 P (6.3245, 108.43°, 3)  ...Cylindrical

To convert   to cylindrical,

 

Ex. 1.13.6 Given point P (-1, 4, 3) and vector  express  and A in cylindrical and spherical coordinates. Evaluate   at P in the cartesian and spherical systems.AU: May-11,Marks 8

Sol. : Refer example 1.13.4 and 1.13.5 for the procedure and verify the answers as :

i) P (√17, 104.036°, 3) in cylindrical.

ii) P(√26, +104.036°, +53.96°) in spherical.

Ex. 1.13.7 Transform the vector 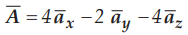 at P (x = + 2, y = + 3, z = 4) to spherical co-ordinate. AU : Dec.-lO, Marks 16

Sol. : Refer example 1.13.4 for the procedure and verify the answer as,

i) P (5.385, 42.03°, 56.31a)

ii)  in spherical system at P

 

Ex. 1.13.8 Transform the vector  at P(x = 2, y = 3, z = 3) to cylindrical co-ordinate. AU : May-14, Marks 8

Sol. : At point P, x = 2, y = 3, z = 3 hence in cylindrical,

r = √x² + y² = √13, ϕ = tan^-1 y/x = 56.31°, z = 3

In this example,

Note that i, j, k are unit vectors in cartesian system and are generally represented as  respectively.

Examples for Practice

Ex. 1.13.9 Give the cartesian co-ordinates of the vector field  at point P (x = 5,y 2,z = -1). 

 

Ex. 1.13.10 Given points A(x = 2, y = 3, z = - 1) and B(ρ = 4, ϕ = - 50°, z = 2) find the distance A to B. [Ans.: 6.7896]

Review Question

1. How to transform the vectors from one coordinate system to other ?