Transformer on Load (M.M.F. Balancing on Load)

Transformer on Load (M.M.F. Balancing on Load )

AU May-08, Dec.-14

• When the transformer is loaded, the current I₂ flows through the secondary winding. The magnitude and phase of I₂ is determined by the load. If load is inductive, I₂ lags V₂. If load is capacitive, I₂ leads V₂ while for resistive load, I₂ is in phase with V₂.

 • There exists a secondary m.m.f. N₂ I₂ due to which secondary current sets up its own flux ϕ₂. This flux ϕ opposes the main flux which is produced in the core due to magnetising component of no load current. Hence the m.m.f. N₂I₂ is called demagnetising ampere-turns. This is shown in the Fig. 6.8.1 (a).

• The flux ϕ₂ momentarily reduces the main flux ϕ, due to which the primary induced e.m.f. E₁ also reduces. Hence the vector difference ???? increases due to which primary draws more current from the supply. This additional current drawn by primary is due to the load hence called load component of primary current denoted as 1'₂ as shown in the Fig. 6.8.1 (b).

• This current I'₂ is in antiphase with 1₂. The current I'₂ sets up its own flux ϕ'₂ which opposes the flux ϕ₂ and helps the main flux ϕ This flux ϕ'₂ neutralises the flux I₂ produced by 1₂. The m.m.f. i.e. ampere turns N₁ I'₂ balances the ampere turns N₂I₂. Hence the net flux in the core is again maintained at constant level.

Key Point: Thus for any load condition, no load to full load the flux in the core is practically constant.

• The load component current I'₂ always neutralises the changes in the load. As practically flux in core is constant, the core loss is also constant for all the loads. Hence the transformer is called constant flux machine.

As the ampere turns are balanced we can write, N₂ I₂ = N₁ 1'₂

                I'₂ = N₂ / N₁ I₂ = K I₂ (6.8.1)

• Thus when transformer is loaded, the primary current I₁ has two components:

1. The no load current I₀ which lags V₁ by angle ϕ₀. It has two components I_m and

I_c.

2. The load component I'₂ which is in antiphase with I₂. And phase of I₂ is decided by the load.

Hence primary current I₁ is vector sum of I₀ and I'₂.

• Assume inductive load, I₂ lags E₂ by ϕ₂, the phasor diagram is shown in the Fig. 6.8.2 (a).

• Assume purely resistive load, I₂ in phase with E₂, the phasor diagram is shown in the Fig. 6.8.2 (b).

• Assume capacitive load, I₂ leads E₂ by ϕ₂, the phasor diagram is shown in the Fig. 6.8.2 (c).

Note that I'₂ is always in antiphase with I₂.

Actually the phase of I₂ is with respect to V₂ i.e. angle ϕ₂ is angle between I₂ and V₂. For the ideal case, E₂ is assumed equal to V₂ neglecting various drops.

The current ratio can be verified from this discussion. As the no load current I₀ is very small, neglecting I₀ we can write, I₁ = I'₂

Balancing the ampere-turns, N₁ I'₂ = N₁ I₁ = N₂ I₂

N₂ /N₁= I₁ /I₂= K

Under full load conditions when I₀ is very small compared to full load currents, the ratio of primary and secondary current is constant.

Ex. 6.8.1 A single phase transformer takes 10 A on no-load at 0.2 p.f. lagging. The turns ratio is 4: 1 (step down). If the load on the secondary is 200 A at a p.f. of 0.85 lagging, find the primary current and power factor. Neglect the voltage drop in the winding. Also draw the phasor diagram. AU May-08, Marks 8

Sol:

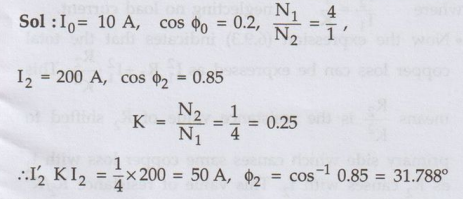
I₂ is in antiphase with I₂ which lags E₂ by 31.788°.

The phasor diagram is shown in the Fig. 6.8.3 (a) with flux ϕ as the reference.

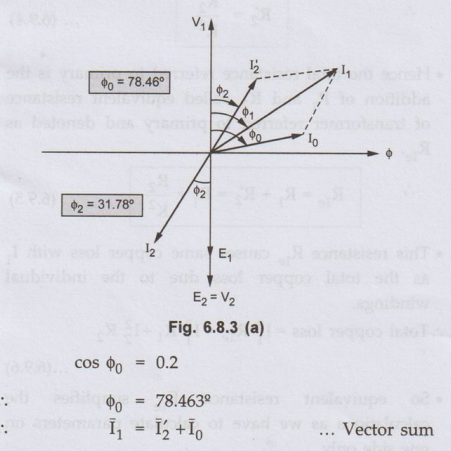
Resolve I₂ and I₀ into two components, along and in quadrature with ϕ

Horizontal component of I₀ = I₀ sin ϕ₀ = 9.798

Vertical component of I₀ = I₀ cos ϕ₀ = 2

Horizontal component of I₂ = I₂ sin ϕ₂ = 26.3388

Review Questions

1. Explain the behaviour of transformer on load. AU: Dec.-14, Marks 8

2. A 400/200 V transformer takes 1 A at a power factor of 0.4 on no load. If the secondary supplies a load current of 50 A at 0.8 lagging power factor, calculate the primary current.

[Ans. : I₁ = 25.874 A, cos ϕ₁ = 0.788 lagging]

3. Explain how the flux in the transformer core remains fairly constant from no load to full load assuming lagging power factor.

4. A 400/200 V, single-phase transformer supplies a load of 50 amps at 0.866 p.f. lagging. The no-load primary current is 2 amp at 0.208 p.f. lagging. Calculate the primary current and primary power factor. Draw the relevant phasor diagram.

 [Ans. I₁ = 26.38 A, cos ϕ₁ = 0.8364 lag]