Transients when the excitation is exponential function

TRANSIENTS WHEN THE EXCITATION IS EXPONENTIAL FUNCTION

Example 20 In the series RL circuit shown in the fig. 3.26, the applied voltage is e = 100 ^50t Find (a) resulting current and (b) initial rate of change of current.

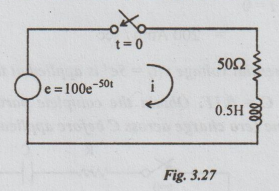
Solution:

In time - domain, the equation describing the above circuit is

Ri + L di/dt = e … (i)

Substituting the values, we get

50i + 0.5 di/dt = 100 e-^50t … (ii)

Taking Laplace transform on both sides, we get

50 I (s) + 0.5s I (s)- 0.5 i₀₊ = 100 / s + 50 … (iii)

i₀₊ = the initial current through inductor = 0 (assumption)

Therefore equation (iii) becomes as

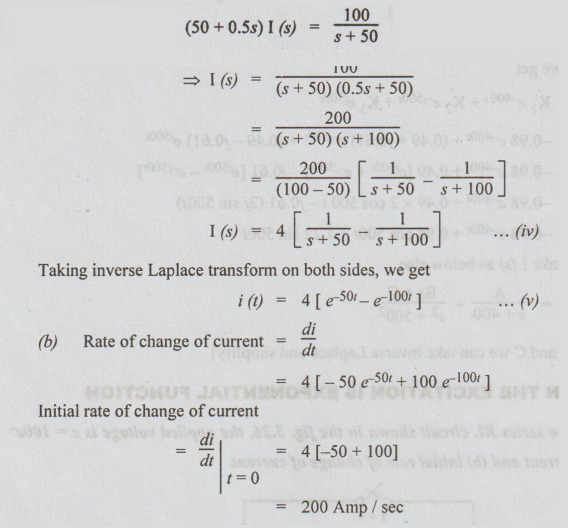
Example 21 An exponential voltage v(t) = 5et is applied at time t = 0 to a series R-C circuit comprising of R = 52 and C = 0.1F. Obtain the complete particular solution for current i (1) through the capacitor. Assume zero charge across C before application of driving voltage.

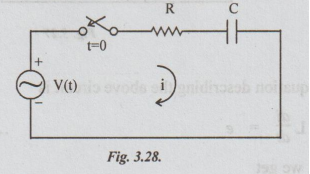
Solution:

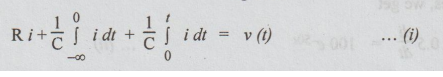
Taking Laplace Transform on both sides,

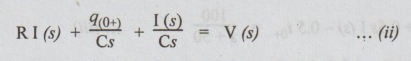
Substituting the values of R, C, 90+ (= 0) and V (s), we get

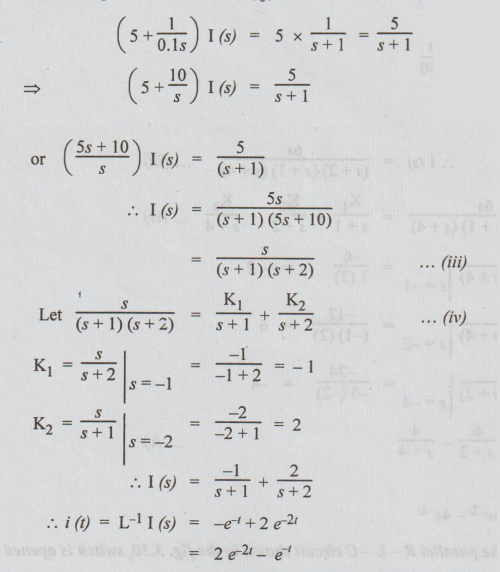
Example 22 In the circuit shown in fig. 3.29, the switch is closed at time t = 0. Obtain i (t). Assume zero current through inductor L and zero charge across C before closing the switch.

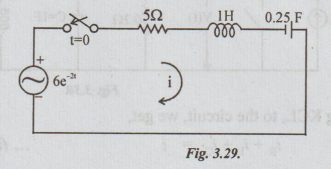
Solution: By KVL, we get

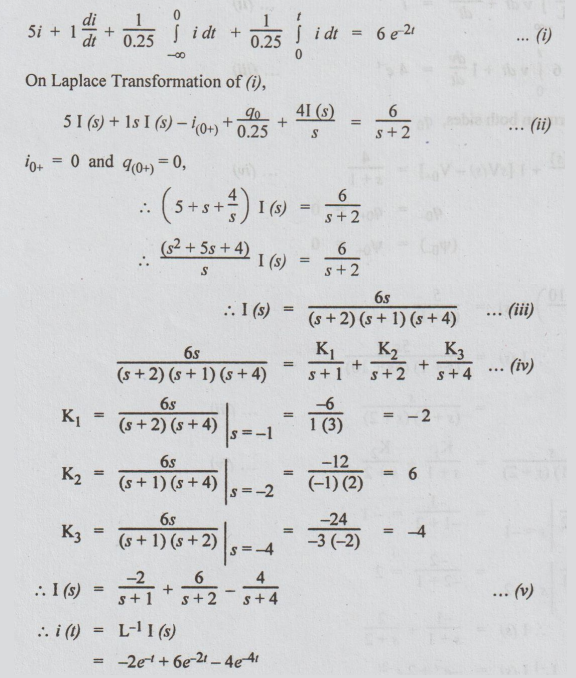
Example 23 In the parallel R-L-C circuit shown in the fig. 3.30, switch is opened at time t = 0. Obtain v (t). Assume that the initial conditions are zero.

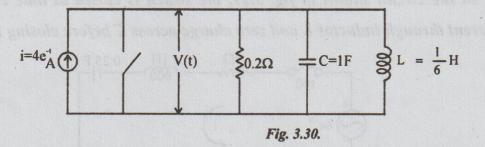
Solution: By applying KCL, to the circuit, we get,

To find the transients using Mesh and Nodal Analysis

In some circuits, there may be many meshes and nodes. In such cases, we can use mesh method and nodal method. In mesh method, KVL is applied and in nodal method, KCL is applied.

Example 24 For the circuit shown in the fig. 3.31, determine the currents i, and is when the switch is closed at t=0. Assume that the initial current through the inductor is 0.

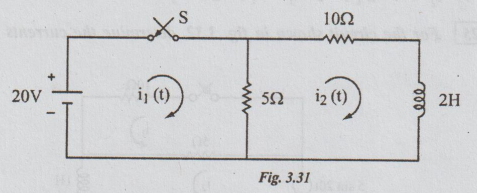
Solution: Let i₁, and i₂ be the mesh currents in the loops 1 and 2 as shown.

By applying Kirchoff's voltage law we get the following equations.

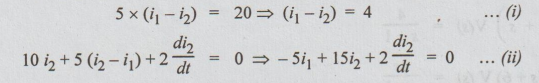
Taking Lapalce transform for equation (i) & (ii) with zero initial current i2, we get the following:

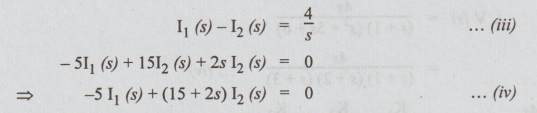
Putting equations (iii) and (iv) in Matrix form we get,

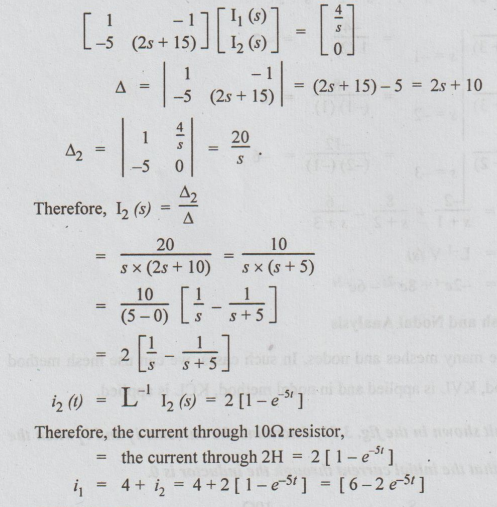
Therefore, the current through 10 Ω resistor,

= the current through 2H = 2 [1-e^-5t]

i₁ = 4 + i₂ = 4 + 2 [1 - e^-5t] = [6 - 2e^-5t]

Example 25 For the circuit shown in fig. 3.32, determine the currents when the switch is closed at t = 0

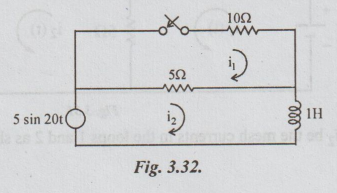
Solution: In S-domain the given circuit is re-drawn as shown in fig. 3.33.

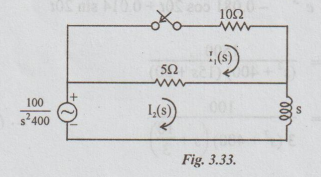
In the matrix form, we write

Example 26 In thefig 3.34, v (t) = 10 volts. Find i2 (t). Assume all initial conditions to be zero. Use Laplace Transform Technique.

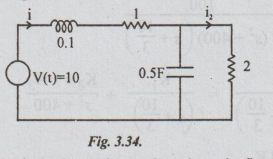
Solution : The circuit in fig 3.35 is re-drwan in s – domain as in fig 3.35.