Trees

Trees

A tree is a finite set of one or more nodes such that -

i) There is a specially designated node called root.

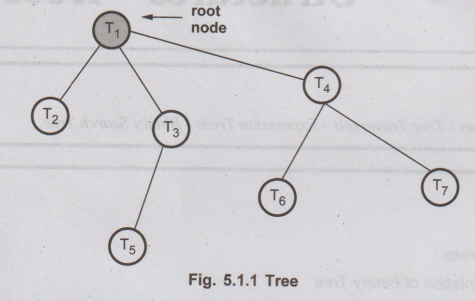
ii) The remaining nodes are partitioned into n> = 0 disjoint sets T₁, T₂,T₃...T_n where T₁, T₂,T₃...T_n are called the sub-trees of the root.

The concept of tree is represented by following Fig. 5.1.1.

Various operations that can be performed on the tree data structure are

1. Creation of a tree

2. Insertion of a node in the tree as a child of desired node.

3. Deletion of any node(except root node) from the tree.

4. Modification of the node value of the tree.

5. Searching particular node from the tree.

 

1. Basic Terminologies

Let us get introduced with some of the definitions or terms which are normally used.

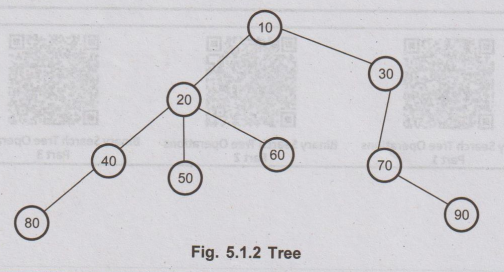
From Fig. 5.1.2,

1. Root

Root is a unique node in the tree to which further subtrees are attached. For above given tree, node 10 is a root node.

2. Parent node

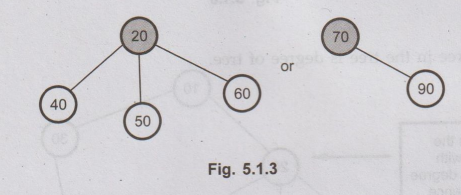
The node having further sub-branches is called parent node. In Fig. 5.1.3 the 20 is parent node of 40, 50 and 60.

3. Child nodes

The child nodes in above given tree are marked as shown below -

4. Leaves

These are the terminal nodes of the tree.

For example -

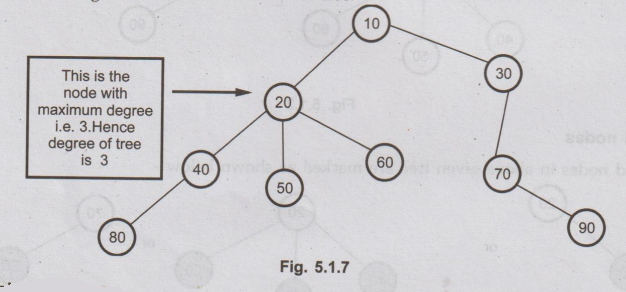
5. Degree of the node

The total number of subtrees attached to that node is called the degree of a node.

For example.

6. Degree of tree

The maximum degree in the tree is degree of tree.

7. Level of the tree

The root node is always considered at level zero.

The adjacent nodes to root are supposed to be at level 1 and so on.

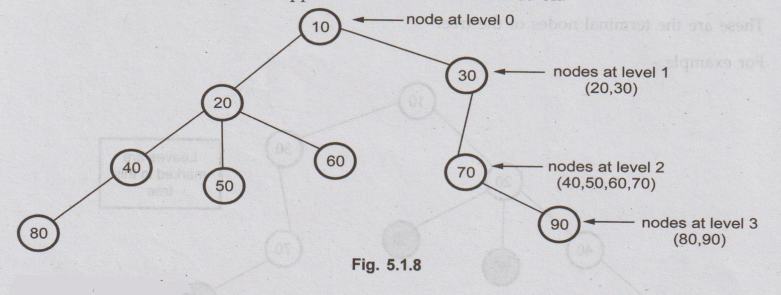
8. Height of the tree

The maximum level is the height of the tree. In Fig. 5.1.8 the height of tree is 3. Sometimes height of the tree is also called depth of tree.

9. Predecessor

While displaying the tree, if some particular node occurs previous to some other node then that node is called predecessor of the other node.

For example: While displaying the tree in Fig. 5.1.8 if we read node 20 first and then if we read node 40, then 20 is a predecessor of 40.

10. Successor

Successor is a node which occurs next to some node.

For example: While displaying tree in Fig. 5.1.8 if we read node 60 after reading node 20 then 60 is called successor of 20.

11. Internal and external nodes

Leaf node means a node having no child node. As leaf nodes are not having further links, we call leaf nodes External nodes and non leaf nodes are called internal nodes.

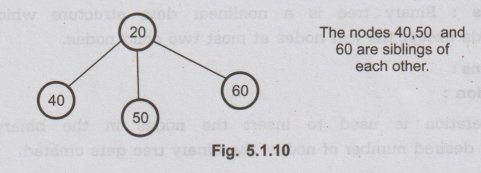
12. Sibling

The nodes with common parent are called siblings or brothers.

For example

In this chapter we will deal with special type of trees called binary trees. Let us understand it.