Triangular Wave Generator using Op-amp

Triangular Wave Generator

We have seen that, the output of integrator is a triangular wave if its input is a square wave. This means that a triangular wave generator can be formed by simply connecting       an integrator to the square wave generator as shown in the Fig. 3.20.1.

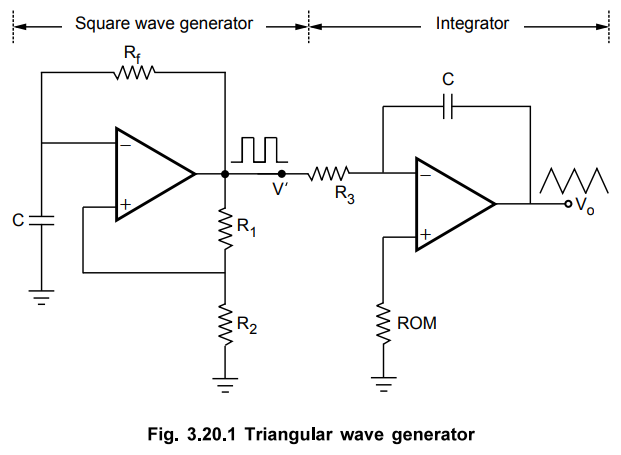
Basically, triangular wave is generated by alternatively charging and discharging a capacitor with a constant current. This is achieved by connecting integrator circuit at the output of square wave generator. Assume that V' is high at + Vsat. This forces a constant current (+ V_sat /R₃) through C (left to right) to drive Vo negative, linearly. When V' is low at -V_sat, it forces a constant current (-V_sat/R₃) through C (right to left) to drive V_o positive, linearly. The frequency of the triangular wave is same as that of square wave. This is illustrated in Fig. 3.20.2. Although the amplitude of the square wave is constant (± V_sat), the amplitude of the triangular wave decreases with an increase in its frequency, and vice versa. This is because the reactance of capacitor decreases at high frequencies and increases at low frequencies. 

In practical circuits, resistance R 4 is connected across C to avoid the saturation problem at low frequencies as in the case of practical integrator as shown in the Fig. 3.20.3

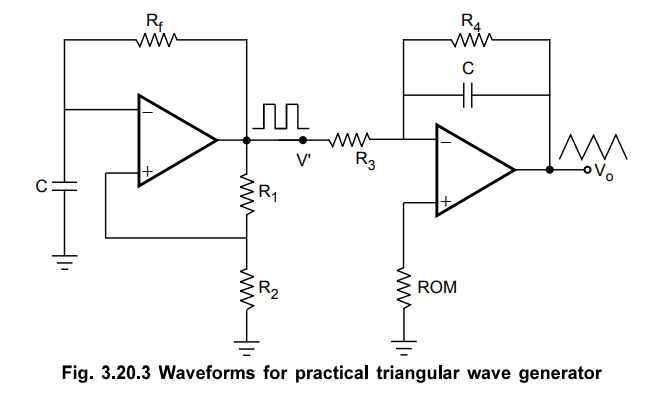
 To obtain stable triangular wave at the output, it is necessary to have 5R3 C2 > T/2, where T is the period of the square wave input.

Another triangular wave generator, which requires fewer components, is shown in the Fig. 3.20.4.

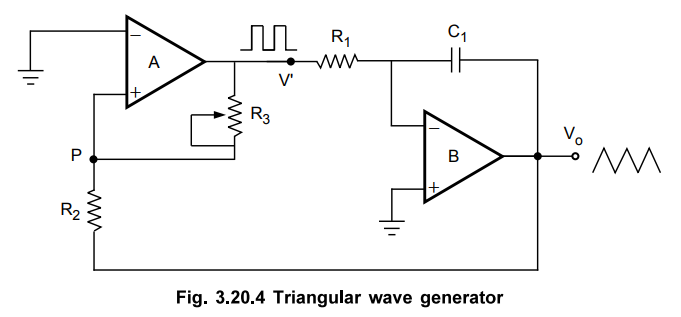
It consists of a comparator (A) and an integrator (B). The output of comparator A is a square wave of amplitude ± Vsat and is applied to the inverting (-) input terminal of the integrator B. The output of integrator is a triangular wave and it is fedback as input to the comparator A through a voltage divider R₂ R₃.

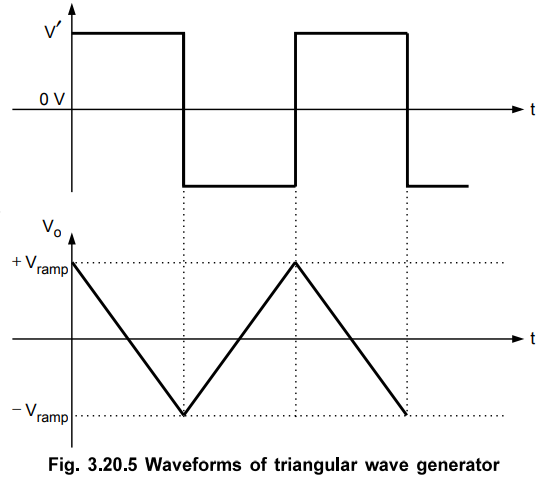
To understand circuit operation, assume that the output of comparator A is at + V_sat- This forces a constant current (+V_sat / R₁) through C to give a negative going ramp at the output of the integrator, as shown in the Fig. 3.20.5. Therefore, one end of voltage divider is at a voltage +V_sat and the other at the negative going ramp. When the negative going ramp reaches a certain value - Vramp, the effective voltage at point p becomes slightly below 0 V. As a result, the output of comparator A switches from positive saturation to negative saturation (-Vsat). This forces a reverse constant current (right to left) through C to give a positive going ramp at the output of the integrator, as shown in the Fig. 3.20.5. When positive going ramp reaches +V_ramp, the effective voltage at point p becomes slightly above 0 V. As a result, the output of comparator A switches from negative saturation to positive saturation (+V_sat). The sequence then repeats to give triangular wave at the output of integrator B.

1. Amplitude and Frequency Calculations

The frequency and amplitude of the triangular wave can be determined as follows : When comparator output is at +Vsat, the effective voltage at point P is given by

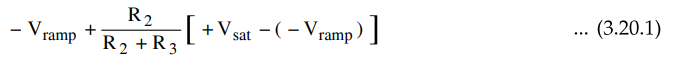
When effective voltage at P becomes equal to zero, we can write above equation as,

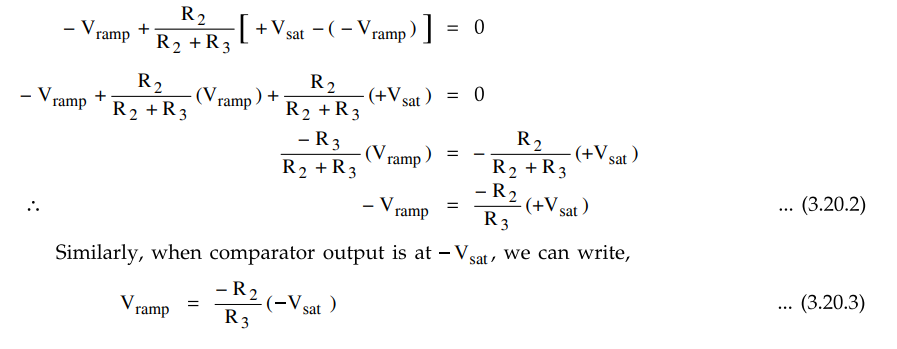
The peak to peak amplitude of the triangular wave can be given as

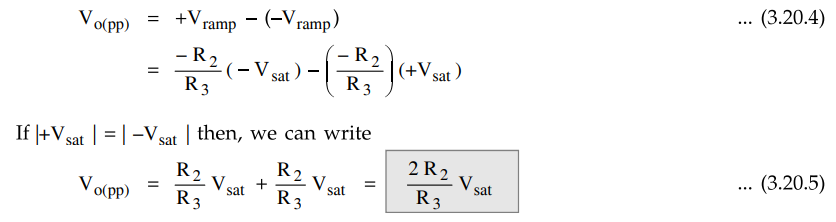
The time taken by the output to swing from – V_ramp, to + V_ramp (or from + V_ramp to

- V_ramp) is equal to half the time period T/2. Refer Fig. 3.20.5. This time can be calculated from the integrator output equation as follows:

Example 3.20.1 Design a triangular wave generator as shown in Fig. 3.20.4 such that fo = 5 kHz and V_o(pp) - 7.5 V. The op-amp saturation voltage is ± 25 V.

Solution :

Example 3.20.2 In a triangular wave generator given R2 = 1.2 kQ, R3 = 6.8 kQ, R1 = 120 ko, C1 = 0.01 μF. Determine the peak to peak output amplitude of triangular C1 wave and frequency of the triangular wave.

Dec.-14, Marks 8

Solution: The peak output amplitude is,

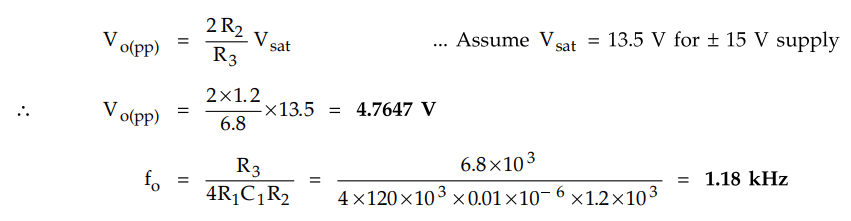
Review Question

1. Draw and explain the operation of a triangular wave generator and obtain an expression for its frequency.