Two Marks Questions with Answers

Two Marks Questions with Answers

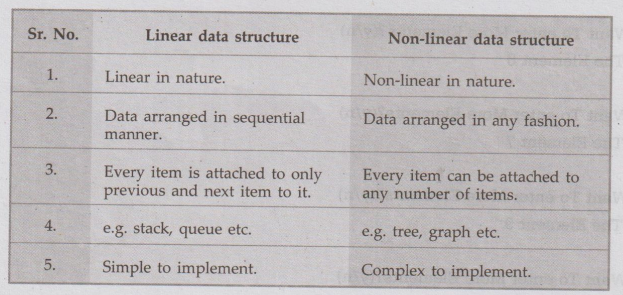
Q.1 What is the difference between linear and non-linear data structures?

Ans. :

 

Q.2 Define: Binary tree.

Ans. :

A binary tree is a finite set of nodes which is either empty or consists of root and two disjoint binary trees called the left subtree and right subtree. Refer Fig.

 

Q.3 Give various implementation of tree.

Ans. : The tree can be implemented by two ways

1. Sequential implementation: The tree is implemented using arrays in this type of implementation.

2. Linked implementation : The tree is implemented or represented using linked list.

 

Q.4 Which tree representation is mostly preferred by the developers linked? Justify.

Ans. :

There are two ways of representing the binary tree - sequential representation and linked representation. The linked representation is normally preferred by developers because in the linked representation the binary tree is represented using linked list. Hence the tree with any number of nodes can be created. Secondly there is no wastage or shortage of the memory in this representation.

 

Q.5 List the applications of trees.

Ans. :

1. In computer networking such as Local Area Network (LAN), Wide Area Networking (WAN), internetworking.

2. In telephone cabling graph theory is effectively used.

3. In job scheduling algorithms the graphs are used.

 

Q.6 In tree construction which is the suitable efficient data structure ?

Ans. :

The linked list is the efficient data structure for constructing the trees. Because using linked list there is no wastage of memory or shortage of memory. The nodes can be allocated or de-allocated as per the requirements.

 

Q.7 What is meant by equivalent binary tree?

Ans. :

The two binary trees are said to be equivalent if the sequence of their traversal is same.

 

Q.8 Define complete binary tree.

Ans. :

A complete binary tree is a tree in which every node except the root node should have exactly two children not necessarily on the same level. Refer Fig. 5.7.1

 

Q.9 What is level of a tree?

AU: Dec.-19

Ans. :

The root node is always considered at level zero. The adjacent nodes to root are supposed to be at level 1 and so on.

 

Q.10 What are internal and external nodes in a tree ?

Ans. :

Leaf node means a node having no child node. As leaf nodes are not having further links, we call leaf nodes external nodes and non-leaf nodes are called internal nodes.

 

Q.11 What is sibling node in a tree?

Ans. :  The nodes with common parent are called siblings or brothers.

 

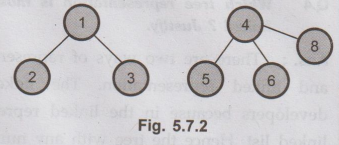
Q.12 What is forest ?

Ans. Forest is a collection of disjoint trees. From a given tree if we remove its root then we get a forest. Refer Fig. 5.7.2.

 

Q.13 What is full binary tree?

Ans. :  A full binary tree is a tree in which every node has zero or two children. Refer Fig. 5.7.3.

 

Q.14 List out the traversal techniques used in tree.

Ans. :

1. Preorder 2. Postorder 3. Inorder traversal

 

Q.15 Which traversal results in elements in sorted order?

Ans. : The inorder traversal results in elements in sorted order.

 

Q. 16 How is binary tree represented using an array ? Give an example.

AU: Dec.-05

Ans. : In an array root node will be at position 1. Its left child will be at position 2 and right child will be at position 3. Hence the nodes of tree are placed in array using following formula -

Parent (n) = floor ((n-1)/2)

left (n) = (2n+1)

right (n) = (2n + 2)

Consider tree as given below.

It will be placed in an array as given below.

 

Q.17 Construct an expression tree for the expression A+ (BC) * D* (E + F).

AU: May-06

Ans. :

 

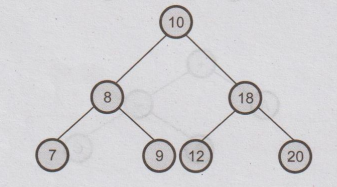
Q.18 Define binary search tree.

AU: May-07, ECE, May-08, Dec.-09, 19

Ans.: Binary search tree is a binary tree in which each node is systematically arranged i.e. the left child has less value than its parent node and right child has greater value than its parent node. The searching of any node in such a tree becomes efficient in this type of tree.

For example -

 

Q.19 List the operations defined on binary trees data type with a suitable example.

Ans. :

Various operations that can be performed on binary trees are - 1. Insertion 2. Deletion 3. Traversal

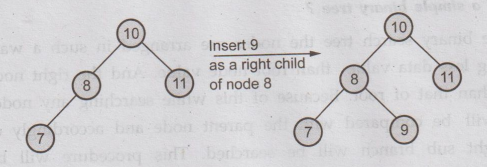
The insertion operation is performed to insert a node at any desired position.

For example -

We can delete any desired node from the binary tree except root node.

For example -

Traversal means a walkover a binary tree. It can be preorder, postorder and inorder traversal.

 

Q.20 Write an algorithm to declare nodes of a tree structure.

Ans. Algorithm :

1. Declare a C structure for the node of a binary tree

typedef struct node

{

int data;

struct node *left;

struct node *right;

}bin;

2. Create a node by allocating memory by using the dynamic memory allocation.

New (bin*)malloc(sizeof(bin));

3. Initialize the Left and Right child pointers to NULL.

New->left=NULL;

New->right=NULL;

Thus a single node gets created. This is the first node of the tree, hence it is called as the root node.

root=New;

4. Attach the next subsequent nodes to either as a left child or a right child to the corresponding parent nodes depending on the user's choice.

 

Q.21 Why it is said that the searching a node in a binary search tree is efficient than that of a simple binary tree?

Ans. : In the binary search tree the nodes are arranged in such a way that the left node is having less data value than root node value. And the right nodes are having larger value than that of root. Because of this while searching any node the value of target node will be compared with the parent node and accordingly either left sub branch or right sub branch will be searched. This procedure will be repeated if required. So one has to compare only particular branches. Thus searching becomes efficient.

 

Q.22 If a binary tree with n nodes is represented sequentially, then for any node with index i (a) 1 ≤ i ≤n, then left child (i) is at 2i, if 2i ≤n. (b) If 2i>n, then I has no left child. Name the type of binary tree which satisfies both (a) and (b).

AU: May-11

Ans. : The complete binary tree.

 

Q.23 What is meant by equivalent binary tree?

AU : May-11

Ans. : The two binary trees are said to be equivalent if the sequence of there traversal is same for example -

The sequence is 8, 8, 9, 10, 11, 12, 13.

 

Q.24 List the applications of trees. AU: Dec.-11

Ans.

Binary tree is used in various applications such as -

1. Binary search tree

2. Game tree

3. Expression tree

4. Threaded Binary tree.

 

Q.25 Define binary tree and give binary tree node structure.

AU: Dec.-12

Ans. : A binary tree is a finite set of nodes which is either empty or consists of root or two disjoint binary trees called the left subtree and right subtree.

Each node in the binary tree contains three fields left child pointer, data field and right child pointer.

Left child    Data    Right child

struct BST

{

BST *leftchild;

int data;

BST *rightchild;

};

 

Q. 26 How many trees are possible with 3 nodes ?

Ans. :

For 3 nodes there are 2³ - 3 trees possible. That means 5 such trees can be drawn. For example - If there are 3 nodes with the value 10, 20, 30 then

 

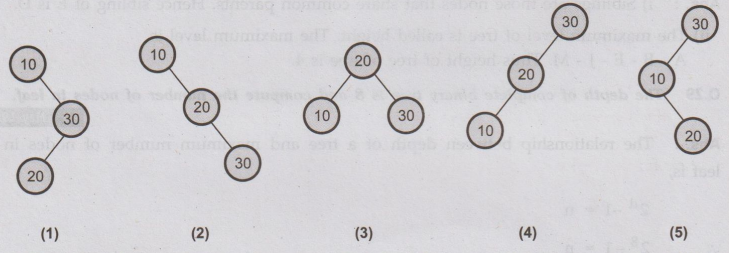
Q. 27 Show the result of inorder traversal of the binary search tree given in Fig. 5.7.4.

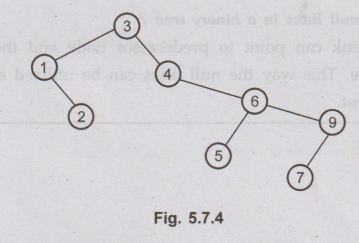
Ans. : Inorder Traversal: 1, 2, 3, 4, 5, 6, 7, 9

 

Q.28 For the tree in Fig. 5.7.5. AU: Dec.-18

a) List the siblings for node E.

b) Compute the height.

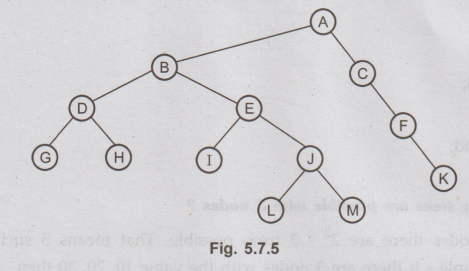Ans. :  i) Siblings are those nodes that share common parents. Hence sibling of E is D.

ii) The maximum level of tree is called height. The maximum level is AB-E-J-M. Thus height of tree of tree is 4.

 

Q. 29 The depth of complete binary tree is 8 and compute the number of nodes in leaf.

 AU: May-19

Ans : The relationship between depth of a tree and maximum number of nodes in leaf is,

2^d -1 = n

2⁸ -1 = n

n = 255

 

Q. 30 How to resolve null links in a binary tree?

AU: May-19

Ans. : The left null link can point to predecessor node and the right null link can point to successor node. This way the null links can be utilized so that tranversing of the tree becomes efficient.