Two Marks Questions with Answers

Two Marks Questions with Answers

Q. 1 What is a scalar quantify ?

Ans. : A scalar is a quantity which is wholly characterized by its magnitude. The various examples of scalar quantity are temperature, mass, volume, density, speed, electric charge etc.

 

Q. 2 What is a vector quantify ?

Ans. : A vector is a quantity which is characterized by both, a magnitude and a direction. The various examples of vector quantity are force, velocity, displacement, electric field intensity, magnetic field intensity, acceleration etc.

 

Q. 3 What is a scalar field ? Give its two examples.

Ans. : A field is a region in which a particular physical function has a value at each and every point in that region. The distribution of a scalar quantity with a definite position in a space is called scalar field. For example the temperature of atmosphere, sound intensity in an auditorium, light intensity in a room, atmospheric pressure in a given region etc.

 

Q. 4 What is a vector field ? Give its two examples.

Ans. : If a quantity which is specified in a region to define a field is a vector then the corresponding field is called a vector field. For example the gravitational force on a mass in a space, the velocity of particles in a moving fluid, wind velocity of atmosphere, voltage gradient in a cable, displacement of a flying bird in a space, magnetic field existing from north to south field etc.

 

Q. 5 What are the sources of electromagnetic fields ?AU: May-11,13,17,19, Dec.-14

Ans. : The main sources of electromagnetic fields are moving charges producing current and current carrying conductors producing magnetic fields. The various practical sources producing such electromagnetic fields are mobile phones, overhead power lines, computers, mobile communication base stations etc.

 

Q. 6 State the elementary vector lengths in three co-ordinate systems.

Ans. : In cartesian system the elementary vector length is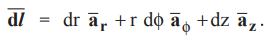 

In cylindrical system it is given as 

While in spherical system it is given as 

 

Q. 7 State the uarious differential surface elements in cartesian co-ordinate system.

Ans. : The various differential surface elements in cartesian co-ordinate system are,

 

Q. 8 State the expressions for differential volume element in three co-ordinate systems.

Ans. : In cartesian system the differential volume element is dv = dx dy dz.

In cylindrical system it is given as dv = r dr dϕ dz

While in spherical system it is given as dv = r² sin θ dr dθ dϕ.

 

Q. 9 State the uarious differential surface elements in cylindrical co-ordinate system.

Ans.  : The various differential surface elements in cartesian co-ordinate system are,

 

Q. 10 How the unit vectors are defined in cylindrical co-ordinate systems ?

Ans. : The  lies in a plane parallel to the xy plane and is perpendicular to the surface of the cylinder at a given point, coming radially outward. The unit vectorlies also in a plane parallel to the xy plane but it is tangent to the cylinder and pointing in a direction of increasing at the given point. The unit vector  is parallel to z axis and directed towards increasing z. 

 

Q. 11 What is unit vector ? What is its function while representing a vector ? (Refer section 1.3.1)

 

Q. 12 Sketch a differential volume element in cylindrical co-ordinates resulting from differential changes in three orthogonal co-ordinate directions. (Refer section 1.7)

 

Q. 13 Give the relation between Cartesian and cylindrical co-ordinate systems. (Refer section 1.7.3)

 

Q. 14 How the unit vectors are defined in spherical co-ordinate systems ?

Ans. : The unit vector  is directed from the centre of the sphere i.e. origin to the given point P. It is directed radially outward, normal to the sphere. It lies in the cone θ = Constant and plane ϕ = Constant. The unit vector  is tangent to the sphere and oriented in the direction of increasing θ. It is normal to the conical surface. The third unit vector  is tangent to the sphere and also tangent to the conical surface. It is oriented in the direction of increasing ϕ. It is same as defined in the cylindrical coordinate system.

 

Q. 15 Sketch a differential volume element in spherical co-ordinates resulting from differential changes in three orthogonal co-ordinate directions. (Refer section 1.8)

 

Q. 16 State the differential lengths in cylindrical co-ordinate system.

Ans. : The differential lengths in cylindrical co-ordinate system are,

 dr = Differential length in r direction

r dϕ = Differential length in ϕ direction

dz = Differential length in z direction

 

Q. 17 State the differential lengths in spherical co-ordinate system.

Ans. : The differential lengths in spherical co-ordinate system are,

 dr = Differential length in r direction

r dθ = Differential length in θ direction

r sin θ dϕ = Differential length in ϕ direction

 

Q. 18 Give the relation between cartesian and spherical co-ordinate systems. (Refer section 1.8.3)

 

Q. 19 Give the differential displacement and volume in spherical co-ordinate system.  AU: Dec.-15

Ans. : The differential displacement in spherial system is

while differential volume is

dv = r² sin θ dr dθ dϕ

 

Q. 20 Define vector or cross product of two vectors. (Refer section 1.11)

 

Q. 21 State the applications of dot product. (Refer section 1.10.2)

 

Q. 22 State any four properties of cross product. (Refer section 1.11.1)

 

Q. 23 Define scalar triple product.

Ans. : The scalar tripple product is defined as,

 

Q. 24 Define vector triple product.

Ans. : The vector tripple product is defined as,

 

Q. 25 Given  Show that the vectors are orthogonal.AU: May-15

Ans. :  (4)(-2) + (6)(4) + (-2)(8) = 0

As dot product is zero, the two vectors are perpendicular i.e. orthogonal.

 

Q. 26 Express in matrix form the unit vector transformation from the rectangular to cylindrical co-ordinate system. AU : May-15

 

Q. 27 Define line integral. (Refer section 1.14.1)

 

Q.28 Define surface integral. (Refer section 1.14.2)

 

Q.29 Define volume integral. (Refer section 1.14.3 )

 

Q.30 State stoke’s theorem. AU: May-04,06,10,12,14,17, Dec.-07,09,13,16

Ans. : The line integral of  around a closed path L is equal to the integral of curl of  over the open surface S enclosed by the closed path L.

Mathematically it is expressed as,

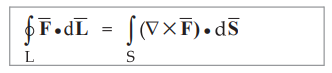
where          dL = Perimeter of total surface S

 

Q. 31 Explain the terms irrotational and solenoidal as applied to vector  AU: Dec.-04,12,May-19.

Ans. : Curl indicates the rotational property of vector field. If curl of vector is zero, the vector field is irrotational. The vector field having its divergence zero is called solenoidal field.

 

Q. 32 State divergence theorem. AU: Dec.-06, 11, 14; May-07, 09, May-11

Ans. : The Divergence theorem states that,

The integral of the normal component of any vector field over a closed surface is equal to the integral of the divergence of this vector field throughout the volume enclosed by that closed surface. Mathematically it is given by,

 

Q. 33 Define divergence of a vector. AU : Dec.-11

Ans.: Mathematically divergence is defined as the net outward flow of the flux per unit volume over a closed incremental surface. It is denoted as div  and given by,

where ΔS = Differential volume element

Divergence of vector field  at a point P is the outward flux per unit volume as the volume shrinks about point P i.e. lim ΔV → 0 representing differential volume element at point P.

Symbolically it is denoted as, 

 

Q. 34 What is gradient of a scalar ? State the gradient in three co-ordinate systems.AU: Dec.-17

Ans. : The operation of the vector operator del () on a scalar function is called gradient of a scalar. Gradient of a scalar is a vector.

The gradient of a scalar W in various co-ordinate systems are given by,

 

Q. 35 State the properties of gradient of a scalar. (Refer section 1.17.1)

 

 Q. 36 State the divergence of a vector in three co-ordinate systems.

Ans. : The divergence of a vector  in three co-ordinate systems is,

 

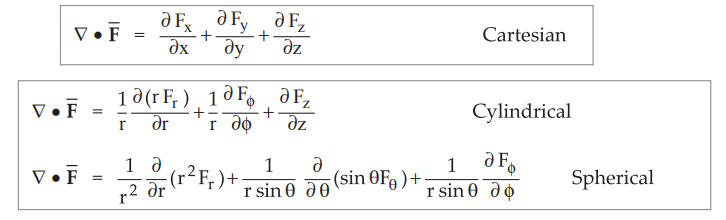
Q. 37 State the curl of a vector in three co-ordinate systems.

Ans. : The curl of a vector  in three co-ordinate systems is,

 

Q. 38 Give practical examples for diverging and curling fields.AU: May-08

Ans. : The flux leaving from an isolated positive charge, flow of heat in a field of varying temperature, air velocity of air flowing out from a punctured tube, velocity of gas flowing out from a hole in a gas balloon are the examples of diverging fields. Magnetic field surrounding the current carrying wire, water velocity in a river, velocity of a rigid body rotating about a fixed axis like a top are the examples of curling fields. 

 

Q. 39 Mention the criteria for choosing an appropriate co-ordinate system for solving a field problem easily. Explain with an examples.          AU: May-07

Ans. : A proper co-ordinate system selection is important for easily solving the field problem. Choosing a proper co-ordinate system can save work and time required for solving the problem.

The criteria for selecting an appropriate co-ordinate system depends on the nature of charge and the distribution of the field.

The point charges are located at points and force exerted on each other is along a line. The line charges are located along the lines. For such cases Cartesian system is proper choice.

For cylindrical conductors and cylindrical surfaces, cables the cylindrical co-ordinate system is preferred.

While for the field distribution in all directions like that of antenna occupying the entire space, spherical conductors, a spherical co-ordinate system is much more easier than other systems.

 

Q. 40 Convert the given rectangular co-ordinate A (x = 2, y = 3, z = 1) into the corresponding cylindrical co-ordinate.

 Ans. : x = 2, y = 3, z = l

τ = √x² + y² = √2² + 3² = √13

ϕ = tan^-1y/x = tan^-13/2= 56.309^o and z = z = 1

 In cylindrical co-ordinates, A (√l3, 56.309°, 1).

 

Q. 41 Given points A (x = 2, y = 3, z = -1) and B (ρ = 4, ϕ = - 50°, z = 2) find the distance from A to B.

Ans. : A(x = 2, y = 3, z = -l) B(ρ = 4, ϕ = - 50°, z = 2)

Convert B into cartesian co-ordinates.

x = ρ cos ϕ= 2.5711, y = ρ sin ϕ = - 3.0641, z = z = 2

AB = √(2- 2.5711)² + (3 - (- 3.064)² + [- 1 - 2]² = 6.7896

 

Q. 42 Find the distance between the points (ρ₁, ϕ₁,z₁) and (ρ₂,ϕ₂, z₂)

 

 

Q. 44 Prove that curl grad ϕ = 0. AU: May-09

 

Q. 45 Verify that the vectors  are parallel to each other.AU: Dec.-09

Ans. : The two vectors are parallel if their cross product is zero.

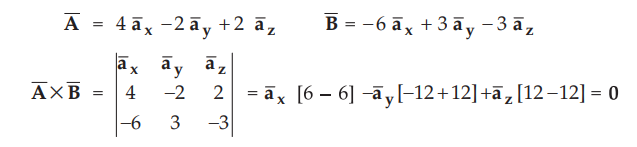
Thus the vectors are parallel to each other.

 

 

Q. 47 Obtain in the cylindrical co-ordinate system the gradient of the function f(r, ϕ, z) = 5r⁴z³ sin ϕ+ cos ϕ+Z² AU : May-12

Ans. : In cylindrical co-ordinates, gradient is

 

Q. 48 Two vectorial quantities  are known to be oriented in two unique directions. Determine the angular separation between them.AU: Dec.-12

 

Q. 49 Convert the point P(3, 4, 5) from cartesian to spherical co-ordinates.AU : Dec.-06

Ans.:

 

Q. 50 State the physical significance of curl of a vector field. AU: May-13

 Ans. : The curl is a closed line integral per unit area as the area shrinks to a point. It gives the circulation per unit area i.e. circulation density of a vector about a point at which the area is going to shrink. Thus curl of a vector at a point quantifies the circulation of a vector around that point. In general if there is no rotation, there is no curl while large angular velocities means greater values of curl. The curl also gives the direction, which is along the axis through a point at which curl is defined. The water velocity in a river, magnetic field lines due to current carrying conductor, the body rotating about a fixed axis are the practical examples of curl.

 

Q. 51 Obtain in the cylindrical co-ordinate system the gradient of the function: f(r, ϕ, z) = 5r⁴z³ sin ϕ AU: May-14

Ans. : In cylindrical system,

 

Q. 52 Points P and Q are located at (0, 2, 4) and (-3, 1, 5). Calculate the distance vector form P to Q. AU: Dec-14

Ans.: 

 

Q. 53 Determine the angle between

 

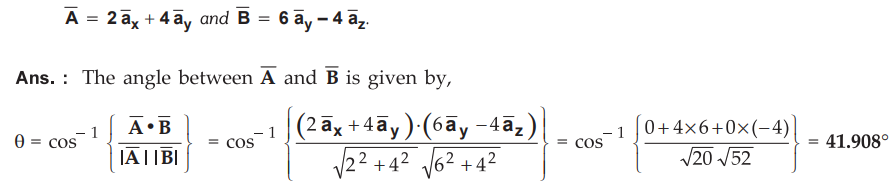
Q. 54 Find the unit vector extending from the orgin towards the point P (3,-1,-22). AU : May-18

Sol. :

 

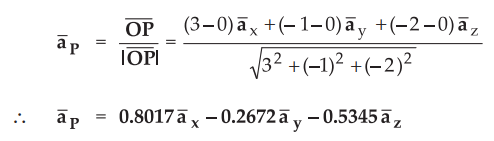
Q. 55 Convert the given point (2,π/2, π /3) in spherical coordinates into cartesian coordinates. AU: Dec.-18

Ans. : r = 2, θ = π/2 = 90°, ϕ = π/3 = 60°, x = r sin θ cos ϕ = 1

y = r sin θ sin ϕ = 1.732, r = r cos θ = 0

Cartesian : (1, 1.732, 0)

 

Q. 56 Given vector field . Find this vector field at P(2, 3, 1) and its projection on . AU: Dec.-19