Two Marks Questions with Answers

Two Marks Questions with Answers

 

Q.1 Define electric flux and electric flux density.

Ans. : The total number of lines of force in any particular electric field is called the electric flux. It is represented by the symbol ψ Similar to the charge, unit of electric flux is also coulomb C. The net flux passing normal through the unit surface area is called the electric flux density. It is denoted as  . It has a specific direction which is normal to the surface area under consideration hence it is a vector field.

 

Q.2 Express the electric flux density at a point in a field in a vector form.

Ans. : The flux density   at a point in a field can be represented in the vector form as,

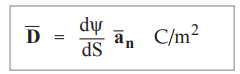
where d ψ = Total flux lines crossing normal through the differential area dS

dS = Differential surface area

  = Unit vector in the direction normal to the differential surface area

 

Q.3 Define electric flux density at a point due to a point charge Q.

Ans. : In the vector form, electric flux density at a point which is at a distance of r, from the point charge + Q is given by,

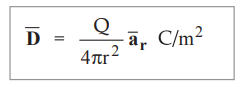
where is the unit vector in the direction of 

 

Q.4 State the relationship between electric field intensity and electric flux density.

Ans. : The electric flux density  and electric filed intensity   are related through the permittivity. If the medium in which charge is located has relative permittivity Ɛ_r then,

 

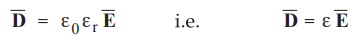
Q.5 State Gauss's law.

AU : May-03, 05, 16, Dec.-07

Ans. : The Gauss's law states that "The electric flux passing through any closed surface is equal to the total charge enclosed by that surface'. Mathematically it is expressed as,

 

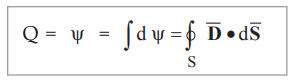
Q.6 What is Gaussian surface ? What conditions it must satisfy ?

Ans. : The surface over which the Gauss's law is applied is called Gaussian surface. Obviously such a surface is a closed surface and it has to satisfy following conditions :

1. The surface may be irregular but should be sufficiently large so as to enclose the entire charge.

2. The surface must be closed.

3. At each point of the surface  is either normal or tangential to the surface.

4. The electric flux density D is constant over the surface at which  is normal.

 

Q.7 State the applications of Gauss's law.

AU : Dec.-04, 13

Ans. : The Gauss's law is used to find 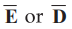 in the following cases,

i) Point charge

ii) Surface charge

iii) Co-axial cable

iv) Spherical shell of charge

v) Uniformly charged sphere

 

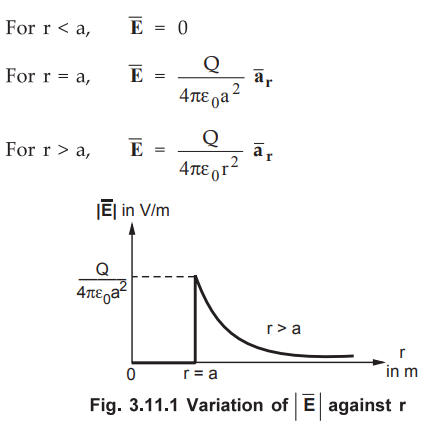
Q.8 State and sketch the variation of  against the radial distance r measured from the origin for the spherical shell of radius 'a'.

Ans. :

 

Q.9 Sketch the variation of  against the radial distance r for a uniformly charged sphere of radius 'a'.

(Refer Fig. 3.7.10 on the page 3-16)

 

Q.10 State the physical significance of divergence of a vector field.

Ans. : The divergence of a vector field Ā is the outflow of the quantity represented by Ā, from a small closed surface per unit volume as the volume shrinks to zero.

Hence the divergence of Ā at a given point is a measure of how much the field represented by Ā diverges or converges from that point. If the field is diverging at point P of vector field Ā, then divergence of Ā at that point P is positive. The  field is spreading out from that point. If the field is converging at the point P, then the divergence of A at the point P is negative. It is practically a convergence i.e. negative of divergence. If the field at point P is such that whatever field is converging, same is diverging from that point P, then the divergence of Ā at point P is zero.

A positive divergence for any vector quantity indicates a source of that vector quantity at that point. A negative divergence for any vector quantity indicates a sink of that vector quantity at that point. A zero divergence indicates there is no source or sink exists at that point.

 

Q.11 Sketch the variation of   against r for a spherical shell of radius 'a'.

(Refer Fig. 3.7.7 on page 3-14)

 

Q.12 State the point form of Gauss's law. Hence state the Maxwell’s first equation.

Ans. : The statement of Gauss's law in point form is,

The divergence of electric flux density in a medium at a point (differential volume shrinking to zero), is equal to the volume charge density (charge per unit volume) at the same point.

The Maxwell's first equation is,

 

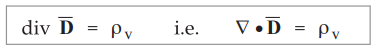
Q.13 State Divergence theorem.

Ans. : The divergence theorem can be state as,

The integral of the normal component of any vector field over a closed surface is equal to the integral of the divergence of this vector field throughout the volume enclosed by that closed surface. Mathematically it is expressed as,

 

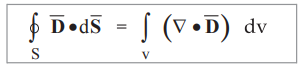
Q.14 Why Gauss’s law cannot be applied to determine the electric field due to finite line charge ?

AU : Dec.-08

Ans. : The Gauss's law cannot be used to find 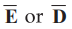 if the charge distribution is not symmetric. The charge distribution is said to be symmetric if the resultant direction of 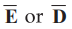 is along only one direction. For example the electric field of infinite line charge is only along cylindrical radial direction . But electric field of the finite line charge has components present in x and y directions and not along any one direction. Hence an electric field of the finite line charge is not symmetrical and hence Gauss’s law can not be applied to it.

 

Q.15 Show by using Gauss’s law :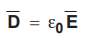 

AU : Dec.-03, May-06

Ans. : Consider charge Q at the origin and   is to be obtained at P, as shown in the Fig. 3.11.2.

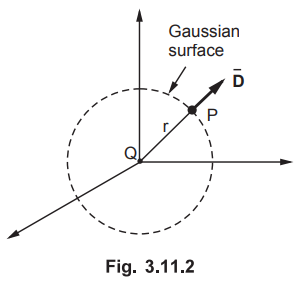
 The D is directed outward in  direction. The Gaussian surface is considered satisfying the required conditions.

Consider dS at point P and spherical co-ordinate system.

 

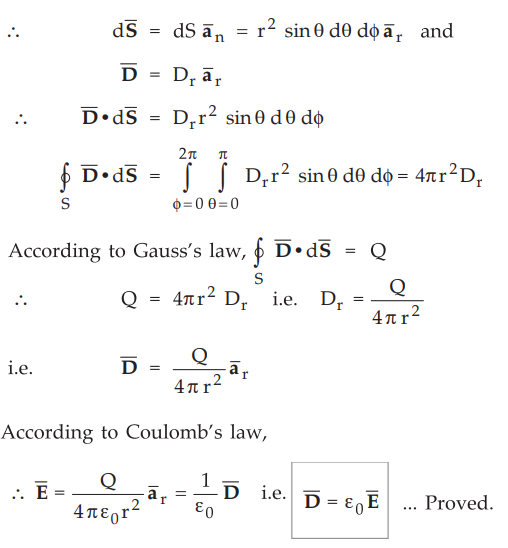
Q.16 Find the total charge enclosed by a cube of 2 m side, centered at the origin with the edges parallel to the axes when  over the cube is 

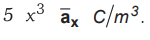
Ans. :         

 

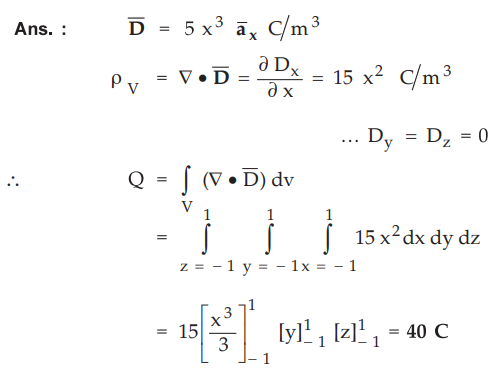
Q.17 Find the electric field intensity in free space if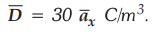 

AU : May-15,18

Ans. :

 

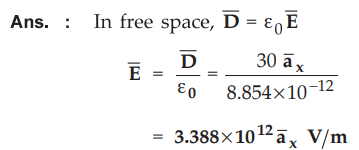
Q.18 A uniform surface charge density pS = 5 nClm2 is situated at x = 2 m plane. What is  at (3, 1, 1) m ?

Ans. :

 

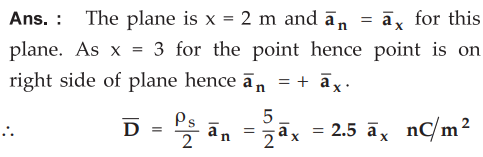
Q.19 A spherical shell of charge density ρs = 2 nC/m² has a radius r = 3 m. Find  at r = 6 m. and r = 1 m.

Ans. : The  for spherical shell of radius ’a’ for r > a is,

 

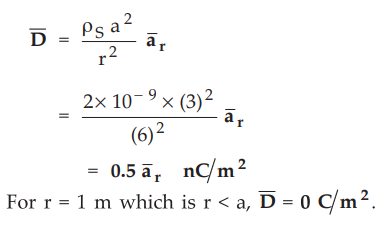
Q.20 A uniformly charged shpere of radius 2 m has charge density of 20 nC/m2. Find  at r = 5 m.

Ans. :

 

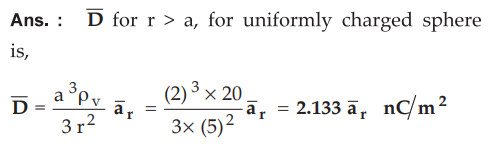
Q.21 A uniform surface charge of p§ =2pC/m2 is situated at z = 2 plane. What is the value of flux density at P (1,1,1) ?

Ans. : ρS = 2µ C/m², P(l, 1, 1), z = 2 plane

The point is below the plane hence

 

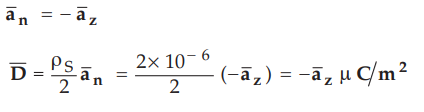
Q.22 What are symmetrical charge distributions ?

AU ; May-09

Ans. : A symmetrical charge distribution is the one whose field varies in one direction, thus its  is a function of only one variable. Similarly the charge density is uniform throughout the surface and at each point of the surface,  is either normal or tangential to the surface. The  is constant over the surface at which  is normal.

 

Q.23 Show that 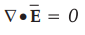 in the case of a point charge.

Ans. :

 

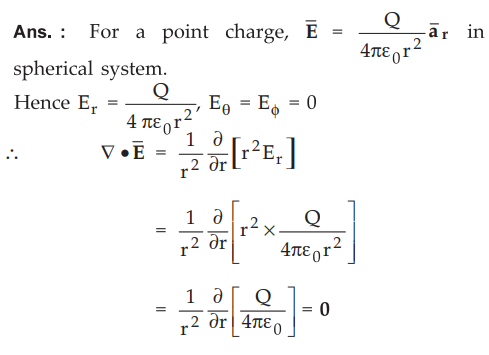
Q.24 State the properties of electric flux lines.

AU : May-13,18, Dec.-14

Ans. :

1. The flux lines start from positive charge and terminate on the negative charge.

2. If the negative charge is absent, the flux lines terminate at infinity. While if positive charge is absent, the flux lines terminate on negative charge from infinity.

3.  The flux lines are parallel and never cross each other.

4. More are the flux lines if electric field is more strong.

5. The flux lines are independent of the medium in which charges are placed.

6. The flux lines enter or leave the charged surface, normally.

 

Q.25 Determine the electric flux density at a distance of 20 cm due to an infinite sheet of uniform charge 20yC/m2 lying on the z = 0 plane.

AU : Dec.-14,18

Ans. :

 

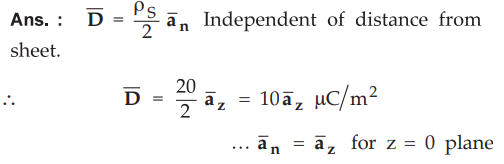
Q.26 Find the magnitude of D for a dielectric material in which E = 0.15 MV/m and Ɛ_r = 5.25.

AU : Dec.-16

Ans. :

| D | = Ɛ | E | = Ɛ0 Ɛr | E |

= 8.854 × 10^-12 × 5.25 × 0.15 × 10⁶= 6.9725 µC/m²