Two Marks Questions with Answers

Two Marks Questions with Answers

 

Q.1 Define potential. AU : May-04, 10, Dec.-14

Ans. : The potential at any point in an electric field is defined as the work done in moving a unit test charge from the infinity (or reference point at which potential is zero) to the point under consideration, against the direction of the field.

 

Q.2 Distinguish between potential and potential difference.

AU : May-04, Dec.-06,12,13,14

Ans. : The potential at any point in an electric field is defined as the work done in moving a unit test charge from the infinity (or reference point at which potential is zero) to the point under consideration, against the direction of the field.

While work done per unit charge in moving unit charge from point B to A in the field  is called potential difference between the points B and A. It is the difference between the absolute potential of points B and A. While specifying potential difference the reference point is not necessary but while specifying the absolute potential the reference is infinity or a point at which potential is zero.

 

Q.3 State the principle of superposition as applied to an electric potential of a point.

Ans. : Consider the various point charges Q₁ Q₂ ... Q_n The potential due to all these point charges, at point A is to be determined. As the potential is scalar, according to the principle of superposition the net potential at point A is the algebraic sum of the potentials at A due to individual point charges, considered one at a time.

where R_n = Distance between point A and position of Q_n

 

Q.4 State the general expressions for the potential at a point due to line charge, surface charge and volume charge.

Ans. : The potential at a point A due to line charge is,

The potential at a point A due to surface charge is,

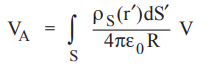
The potential at a point A due to volume charge is

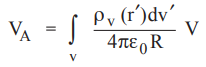
Note that for uniform line charge, line charge density ρL(r') = ρL, uniform surface charge density P S(rz) = P S while uniform volume charge density ρv(r') = ρv.

 

Q.5 State the potential difference between the two points due to infinite line charge.

Ans. : Consider an infinite line charge having uniform line charge density ρL C/m. The point B is at a radial distance r_B while point A is at a radial distance r_A from the charge. Then the potential difference between the points A and B is given by,

 

Q.6 What is an equipotential surface ?

Ans. : An equipotential surface is an imaginary surface in an electric field of a given charge distribution, in which all the points on the surface are at the same electric potential.

The potential difference between any two points on the equipotential surface is always zero. Thus the work done in moving a test charge from one point to another in an equipotential surface is always zero. There can be many equipotential surfaces existing in an electric field of a particular charge distribution.

 

Q.7 Show the equipotential surfaces for a point charge.

(Refer Fig. 4.10.1)

 

Q.8 State the nature of conservative field.

AU : May-05,19, Nov.-05, Dec.-17

Ans. : Any field that satisfies the equation of the form

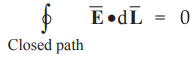
i.e closed line integral of the field is zero, is called conservative field. For such a field no work is done or no energy is conserved around a closed path. This indicates that the work done in  and hence potential between any two points is independent of the path joining the two points. Earth's gravitational field and static electric field are the example of conservative field. For a nonconservative field the line integral around certain closed paths may be zero but it is not zero for each and every closed path. The time varying electric and magnetic fields, velocity field of particles on a rim of rotating wheel, force due to friction are nonconservative fields.

 

Q.9 Give the relation between electric field and potential.

AU : May-07, Dec.-07

Ans. : The electric field is the negative gradient of potential. Mathematically it is given by,

 

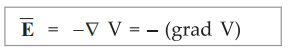
Q.10 Give the gradient of a scalar in all the co-ordinate systems.

(Refer section 4.12.2)

 

Q.11 Give the energy in terms of . Also give the expression for the energy density.

Ans. : The energy in terms of  is given by,

While the energy density in the electric field is given by,

 

Q.12 What is an electric dipole ?

Ans. : The two point charges of equal magnitude but opposite sign, separated by a very small distance give rise to an electric dipole.

 

Q.13 Give an electric field  at a point due to an electric dipole.

Ans. : An electric field  at a point due to an electric dipole is given by,

Q.14 Define dipole moment. Give its units.

Ans. : The vector length directed from - Q to + Q charge in an electric dipole is denoted as d. Then the product Q  is called dipole moment and denoted as  

 

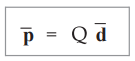
Q.15 Give the potential at a point due to an electrical dipole.

AU : Dec.-10

Ans. : The expression of potential V due to an electric dipole is,

where V - Potential due to an electrical dipole

d - Distance between the two charges

r - Distance between point and the origin.

 

Q.16 Define equipotential line and show that equipotential and field lines are orthogonal.

AU ; May-06, 01

(OR)

Why the direction of electric field is always normal to equipotential surface ?

Ans. : The potential difference is given by,

Now if  is choosen such that point Q moves to P along perpendicular direction . The dot product of two perpendicular vectors is zero.

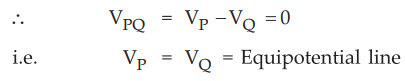
Thus an equipotential line is perpendicular to  field lines. Hence equipotential line and field lines are always orthogonal i.e. perpendicular

 

Q.17 Give examples for uniform and non-uniform electric fields.

Ans. : An electric field in which electric field lines are parallel is called uniform electric field. In a nonuniform field the field lines diverge, going from a stronger to a weaker field region.

The field between two charged plates, a field of a parallel plate capacitor are uniform fields. When electrons start to be pushed together in a cloud, they cause a charge separation to occur in the ground below the cloud. This forms a strong electric field between cloud and the ground. This is uniform electric field.

While the electric field which varies with  distance is a nonuniform. Thus field due to a point charge, field of a spherical capacitor are nonuniform electric fields.

Q.18 A point charge + 2 nC is located at the origin. What is the value of potential at P(l, 0, 0) m ?

AU : May-11

Ans. : Q = 2 nC, P (1, 0, 0), Q is at origin.

 

Q.19 An electric dipole of 100  pC.m is located at the origin. Find the scalar potential V at the point (0,0,10).

Ans. :

 

Q.20 The potential distribution of

V = ax² + 6y² - 3√V exists in an electric field 

Sol . :

 

Q.21 The electric potential near the origin of a system of co-ordinates is V = ax² + by² + cz². Find the electric field at (1, 2, 3).

Ans.:

 

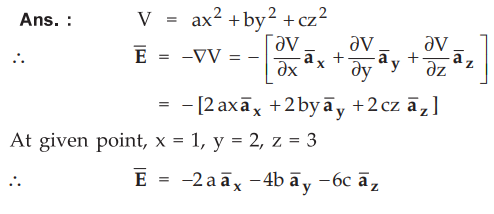
Q. 22 The electric potential near the origin of a system of co-ordinates is V = 5x² + 8 y² + 10z². Find the electric field at (1, 2, 3).

Ans. :