Two Marks Questions with Answers

Two Marks Questions with Answers

 

Q.1 Define magnetic field and magnetic fines of force.

Ans. : The region around a magnet within which the influence of the magnet can be experienced is called magnetic field. Such a field is represented by imaginary lines around the magnet which are called magnetic lines of force. These lines of force are also called magnetic lines of flux or magnetic flux lines.

 

Q.2 State right hand thumb rule.

Ans. : Right hand thumb rule states that, hold the current carrying conductor in the right hand such that the thumb pointing in the direction of current and parallel to the conductor, then curled fingers point in the direction of the magnetic lines of flux around it.

 

Q.3 Define magnetic field intensify and state its unit.

AU : Dec.-04

Ans. : The magnetic field intensity at any point in the magnetic field is defined as the force experienced by a unit north pole of one weber strength, when placed at that point. Magnetic field intensity is measured in newtons/weber (N/Wb) or amperes per metre (A/m) or ampere-tums/metre (AT/m). It is denoted as.

 

Q.4 Define magnetic flux density and state its unit.

Ans. : The total magnetic lines of force i.e. magnetic flux crossing a unit area in a plane at right angles to the direction of flux is called magnetic flux density. It is denoted as B and is a vector quantity. It is measured in weber per square metre.

(Wb/m²) which is also called Tesla (T).

 

Q.5 What is permeability ? State its unit.

Ans. : Permeability is the ability or ease with which the current carrying conductor forces the magnetic flux through the region around it. For a free space, the permeability is denoted as µ0 and its value is 4π × 10^-7. The permeability p is measured in henries per metre (H/m). For any other region, a relative permeability is specified as µ = µ0 µr.

 

Q.6 What is the relation between magnetic flux density and magnetic field intensity ?

AU : Dec.-02, May-04

Ans. : In magnetostatics, the magnetic flux density and magnetic field intensity   are related to each other through the property of the region in which current carrying conductor is placed called permeability denoted as µ.

 

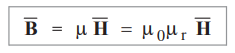
Q.7 State Biot-Sauart's law.

AU ; Dec.-03, 06, 09, 14, May-05, 10, 17

Ans. : The Biot-Savart law states that,

The magnetic field intensity  produced at a point P due to a differential current element IdL is,

1. Proportional to the product of the current I and differential length dL.

2. The sine of the angle between the element and the line joining point P to the element.

3. And inversely proportional to the square of the distance R between point P and the element.

Mathematically it is represented as,

To obtain total magnetic field intensity , the above equation takes the integral form as,

 

Q.8 State the expression for  on the axis of a circular loop placed in x-y plane. Hence find the  at the centre of the loop.

Ans. : The expression for  on the axis of a circular loop placed in x-y plane is,

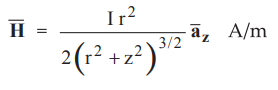
where          r = Radius of the circular loop and

z = Distance of point along the axis

If point is shifted at the centre of the circular loop i.e. z = 0,

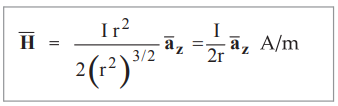
 where  is the unit vector normal to xy plane in which the circular loop is lying.

 

Q.9 State Ampere's circuital law.

AU : Dec.-04, 16, 17, May-07, 09, 11, 12, 14, 16

Ans. : The Ampere's circuital law states that,

The line integral of magnetic field intensity around a closed path is exactly equal to the direct current enclosed by that path.

The mathematical representation of Ampere's circuital law is,

 

Q.10 Sketch variation of  against r in co-axial cable.

(Refer Fig. 7.9.5 on page 7-21)

 

Q.11 What is  at a point due to current sheet of density A/m ?

Ans. : For an infinite sheet of current density point is

 

Q.12 State the expression for in all the regions if a cylindrical conductor carries a direct current I and its radius is 'R'm.

Ans. : For a cylindrical conductor carrying a direct current I with radius 'R'm,

 

Q.13 State the point form of Ampere's circuital law.

Ans. : The point form of Ampere's circuital law is,

 

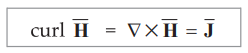
Q.14 State Gauss's law for magnetic fields.

Ans. : The integral  evaluated over a closed surface is always zero.

This is called law of conservation of magnetic flux or Gauss's law in integral form for magnetic fields.

The Gauss's law in differential form for magnetic fields is given by,

The divergence of magnetic flux density is always zero.

 

Q.15 What is scalar magnetic potential ?

AU : Dec.-03, May-05

Ans. : The scalar magnetic potential Vm can be defined for source free region where   i.e. current density is zero.

Magnetic scalar potential can be expressed interms of  as,

 

Q.16 State Laplace's equation for scalar magnetic potential.

Ans. : The Laplace's equation for scalar magnetic potential is,

 

Q.17 Define vector magnetic potential and state its unit.

AU : Dec.-03, May-04, 06, 17

Ans. : The vector magnetic potential Ā is defined such that curl of vector magnetic potential is the flux density.

The definition requires that . The vector magnetic potential Ā serves as an intermediate quantity from which  and hence  can be obtained. It is measured in Wb/m.

 

Q.18 Deduce the expression for the current density form the vector magnetic potential.

Ans.:

Using vector identity to express left hand side we can write,

 

Q.19 State the Poisson’s equation for magnetostatic fields.

Ans. : The Poisson's equation for magnetostatic fields.

 

Q.20 Can a static magnetic field exist in a good conductor ? Explain.

Ans. : A static magnetic field can exist in a good conductor. When conductor carries current, it produces the flux which can exist inside the conductor. Due to this flux, magnetic field and intensity exists at a point inside the good conductor.

 

Q.21 Plot the variation of  inside and outside a circular conductor with uniform current density.

(Refer Fig. 7.9.9 on page 7-23)

 

Q.22 Plane y = 0 carries a uniform current of 30   Calculate the magnetic field intensity at (1, 10, -2) m in rectangular co-ordinate system.

Ans. : For an infinite current sheet, 

Key Point : The point (1, 10, -2) is to the right of plane y = 0. Hence 

 

Q.23 What should be the direction of currents (of same magnitude) in two identical co-axial cylindrical coils to have maximum magnitude of  at a point on the axis ?

Ans. : The direction of currents in two identical co-axial cylindrical coil must be same, to have maximum magnitude of B at a point on the axis. This can be confirmed using right hand thumb rule.

 

Q.24 State the applications of Ampere's circuital law.

AU : Dec.-07

Ans. : Ampere's circuital law can be used to obtain  due to,

a) Infinitely long straight conductor

b) Co-axial cable

c) Infinite sheet of current

d) Circular conductor carrying current I.

 

Q.25 Draw the magnetic filed pattern in and around a solenoid.

Ans. : Consider a solenoid and field pattern around it as shown in the Fig. 7.14.1.

 

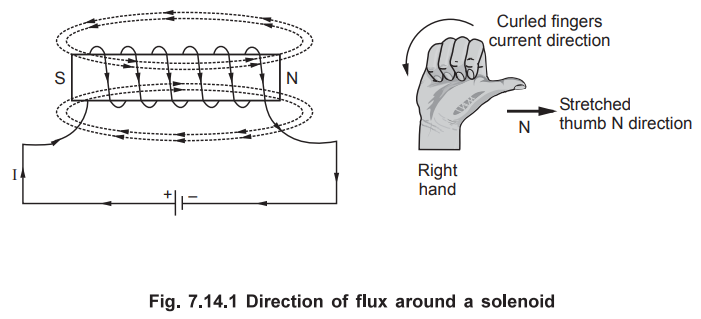
Q.26 Define magnetic flux and flux density.

Ans. : The total number of lines of force existing in a particular magnetic field is called magnetic flux which is denoted as ϕ.

 

The flux per unit area in a plane at right angles to the flux is called magnetic flux density. It is shown in the Fig. 7.14.2 and denoted as B.

 

Q.27 For the configuration shown calculate the value of

AU : May-07

Ans. : According to the Ampere’s circuital law

= Current enclosed by closed path

The current enclosed is + 100 A (outwards) and -10 A (inwards)

i.e. total 100 - 10 = 90 A.

The current shown outside the closed path has no effect on the integral.

 

Q.28 A long straight wire carries a current 1 = 1 amp.

At what distance is the magnetic field H = 1 A/m.

AU : May-09

Ans . : 1 = 1 A, H = 1 A/m

For a long straight wire the  is given by,

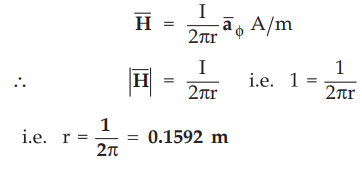
At the perpendicular distance of 0.1592 m from the wire,  will be 1 A/m.

 

Q.29 Find the value of magnetic field intensify at the centre of a circular loop of radius 1 m carrying a current of 10 A.

AU : May-13, Dec.-14

Ans. :

where  = Unit vector normal to plane of circular loop.

 

Q.30 Compare coulomb's law and Biot-savart law.

Ans. : There are certain similarities and differences between Coulomb's law and Biot Savart law which are given in the following table.

 

Q.31  Write down the expression for magnetic field at the centre of the circular coil.

AU : Dec.-19

Ans. : It is given by,

Where   = Unit vector perpendicular to the plane containing the coil

R = Radius, I = Current

 

Q.32  Distinguish between magnetic scalar potential and magnetic vector potential.

Ans.