Two Reaction Theory for Synchronous Motor

Two Reaction Theory for Synchronous Motor

The two reaction theory discussed earlier is applicable to the synchronous motors. The two reactances according to this theory are direct axis reactance X_d and quadrature axis reactance X_q. The motor armature current has two components Id and I_q. The phasor diagram for the synchronous motor with a lagging power factor is shown in the Fig. 4.15.1. 

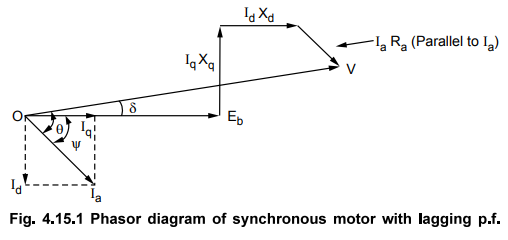
The phasor I_q X_q is such that I_q lags I_qX_q by 90° while the phasor I_dX_d is such that Id lags I_dX_d by 90°. The angle between V and E_b is δ, V and I_a is θ and E_b and I _a  is ψ The phasor diagram can be further modified as shown in the Fig. 4.15.2.

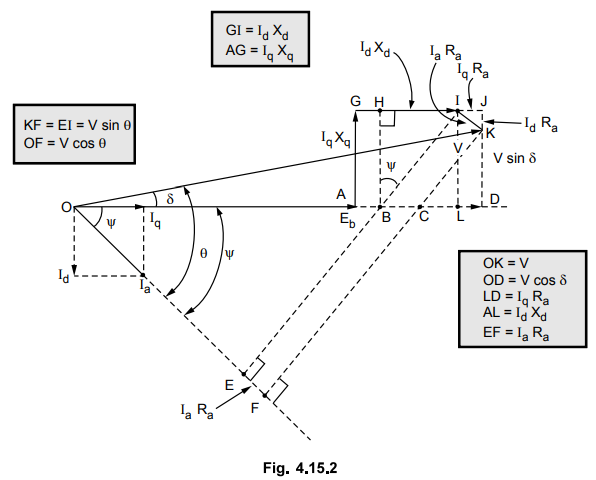
The expression of dp_m /dδ gives the rate of change of power with respect to load angle δ and is called stability factor, rigidity factor or the stiffness of coupling.

Using cos 2 δ = cos² δ -1 m the equation (4.15.10) and solving it, δ for maximum power is given by,

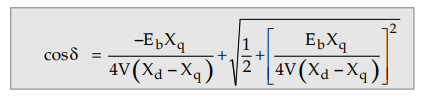
The expression is obtained by neglecting armature resistance.

Example 4.15.1 A 6600 V, 2720 h.p. 3 phase star connected, synchronous motor has Xd=5 Ω /ph and Xq =3.1 Ω /ph. Neglecting all the losses, calculate the excitation e.m.f. when motor supplies rated load at 0.8 p.f. lagging. Also calculate the maximum power that motor would develop for this excitation.

Solution :

V_L = 6600 V, P_out = 2720 h.p. = 2720 × 735.5 W ≈ 2 MW

As all losses are to be neglected, P_in = P_out = 2 MW

Example 4.15.2 A 1500 kW, 3 phase, star connected, 3.3 kV synchronous motor has reactance of xd = 4.01 and xq = 2.88 Q per phase. All losses may be neglected. Calculate the excitation e.m.f. when the motor is supplying rated load at unity p.f. Also calculate the maximum mechanical power that the motor can supply with excitation held fixed at this value. AU : May-08, Marks 12

Solution :

Examples for Practice

Example 4.15.3 From the phasor diagram of an over excited salient pole synchronous motor, prove the following relations.

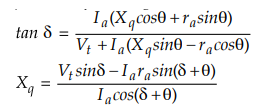
where δ and θ are load and power factor angle respectively.

Example 4.15.4 A 1800 kVA, star connected, 6.6 kV salient poles synchronous motor has Xd = 23.2 Q and Xq = 14.5 Q per phase. Its Ra is zero. Calculate the excitation e.m.f. when the motor is supplying rated load at 0.8 pf. leading. If the excitation is cut- off, find the maximum load that the motor can supply.    

[Ans.: (P_m)_max = 0.1502 MW per phase]

Example 4.15.5 A 6.6 kV, 3-phase, star-connected synchronous motor is running in parallel with an infinite bus. Its direct and quadrature-axis synchronous reactances are 10 Q and 5 Q, respectively. If the field current is reduced to zero, find the maximum load that can be put on the synchronous motor. Also calculate the armature current and the maximum power developed. Neglect armature resistance.

[Ans.: 2178 kW, 602.4921 A] 

Example 4.15.6 The full-load torque angle of a synchronous motor at rated voltage and frequency is 30° electrical. The stator resistance is negligible. How would the torque angle be affected by following changes ?

i) The load torque and terminal voltage remaining constant, the excitation and frequency are raised by 10 %.

ii) The load power and terminal voltage remaining constant, the excitation and frequency are reduced by 10 %.

iii) The load torque and excitation remaining constant, the terminal voltage and frequency are raised by 10 %.

iv) The load power and excitation remaining constant, the terminal voltage and frequency are reduced by 10 %.

[Ans.: i) 33.36°, ii) 30°, iii) 33.36°, iv) 30°]

Example 4.15.7 From the phasor diagram of the lagging p.f. salient pole sychronous motor, show that :

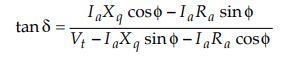
where the symbols having their usual meanings.

Example 4.15.8 A salient-pole synchronous motor has X_d = 0.85p.u. and X_q = 055p.u. It is connected to bus-bars of 1.0 p.u. voltage while its excitation is adjusted to 1.2 p.u. Calculate the maximum power output, the motor can supply without loss of synchronism. Compute the minimum p.u. excitation that is necessary for the machine to stay in synchronism while supplying the full-load torque (i.e. 1.0 p.u. power).

[Ans.: 1.5328 p.u., 0.706 p. u]

Review Question

1. Explain the two reaction theory for synchronous motor.