Types of Charge Distributions

Types of Charge Distributions

• Uptill now the forces and electric fields due to only point charges are considered. In addition to the point charges, there is possibility of continuous charge distributions along a line, on a surface or in a volume. Thus there are four types of charge distributions which are,

1. Point charge 2. Line charge 3. Surface charge 4. Volume charge

1. Point Charge

• It is seen that if the dimensions of a surface carrying charge are very very small compared to region surrounding it then the surface can be treated to be a point. The corresponding charge is called point charge. The point charge has a position but not the dimensions. This is shown in the Fig. 2.4.1 (a) The point charge can be positive or negative.

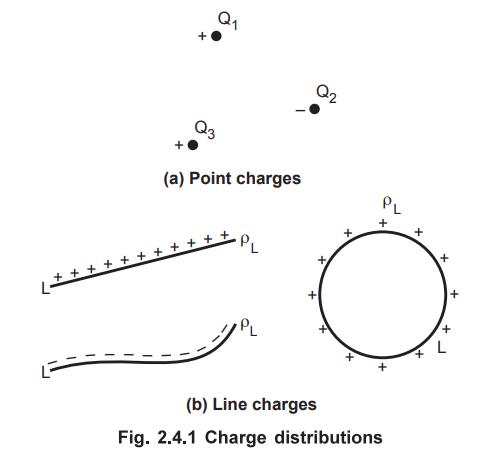
2. Line Charge

• It is possible that the charge may be spreaded all along a line, which may be finite or infinite. Such a charge uniformly distributed along a line is called a line charge. This is shown in the Fig. 2.4.1 (b).

• The charge density of the line charge is denoted as ρ_L and defined as charge per unit length.

ρ_L = Total charge in coulomb/Total length in metres (C/m)

• Thus ρ_L is measured in C/m. The ρ_L is constant all along the length L of the line carrying the charge.

a. Method of Finding Q from ρ_L

• In many cases, ρ_L is given to be the function of coordinates of the line i.e. ρ_L = 3x or ρ_L = 4y² etc. In such a case it is necessary to find the total charge Q by considering differential length dZ of the line. Then by integrating the charge dQ on dZ, for the entire length, total charge Q is to be obtained. Such an integral is called line integral.

• Mathematically, dQ = ρ_L dl = Charge on differential length dl

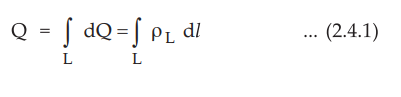
• If the line of length L is a closed path as shown in the Fig. 2.4.1 (b) then integral is called closed contour integral and denoted as,

• A sharp beam in a cathode ray tube or a charged circular loop of conductor are the examples of line charge. The charge distributed may be positive or negative along a line.

Ex. 2.4.1 A charge is distributed on x axis of cartesian system having a line charge density of 3x₂ µC/m. Find the total charge over the length of 10 m.

Sol. : Given ρ_L = 3x² μC/m and L = 10 m along x axis.

The differential length be dZ = dx in x direction and corresponding charge is dQ = ρ_L dl = ρ_L dx

= 1000 μC = 1 mC

3. Surface Charge

• If the charge is distributed uniformly over a two dimensional surface then it is called a surface charge or a sheet of charge. The surface charge is shown in the Fig. 2.4.2.

• The two dimensional surface has area in square metres. Then the surface charge density is denoted as ρ_s and defined as the charge per unit surface area.

ρ_s = Total charge in coulomb/ Total area in square metres (C/m²)

• Thus ρ_S is expressed in C/ m² .The p s is constant over the surface carrying the charge.

a. Method of Finding Q from ρ_s

• In case of surface charge distribution, it is necessary to find the total charge Q by considering elementary surface area dS. The charge dQ on this differential area is given by p S dS. Then integrating this dQ over the given surface, the total charge Q is to be obtained. Such an integral is called a surface integral and mathematically given by,

• The plate of a charged parallel plate capacitor is an example of surface charge distribution. If the dimensions of the sheet of charge are very large compared to the distance at which the effects of charge are to be considered then the distribution is called infinite sheet of charge.

4. Volume Charge

• If the charge distributed uniformly in a volume then it is called volume charge. The volume charge is shown in the Fig. 2.4.3.

• The volume charge density is denoted as p v and defined as the charge per unit volume.

ρ_v = Total charge in coulomb / Total volume in cubic metres (C/m³)

• Thus ρ_v is expressed inC/m³.

Method of Finding Q from ρ_v

• In case of volume charge distribution, consider the differential volume dv as shown in the Fig. 2.4.3. Then the charge dQ possessed by the differential volume is ρ_vdv. Then the total charge within the finite given volume is to be obtained by integrating the dQ throughout that volume. Such an integral is called volume integral. Mathematically it is given by.

• The charged cloud is an example of volume charge.

Key Point : In all the integrals line, surface and volume a single integral sign is used but practically for surface integral it becomes double integration while to integrate throughout the volume it becomes triple integration. Similarly ρ_s and ρ_v can be functions of the co-ordinates of the system used e.g. ρ_s = 4xy C/m², ρ_v = 20z e^-0.2y C/m³ etc.

Ex. 2.4.2 A uniform volume charge density of 0.2 μC/m³ is present throughout the spherical shell extending from r = 3cm to r = 5 cm. If ρ_v = 0 elsewhere, find :

i) Total charge present throughout the shell.

ii) r₁ if half the total charge is located in the region 3 cm < r <  r₁.

Sol. :  ρ_v = μC/m³, dv = r² sin θ dr dϕ for spherical

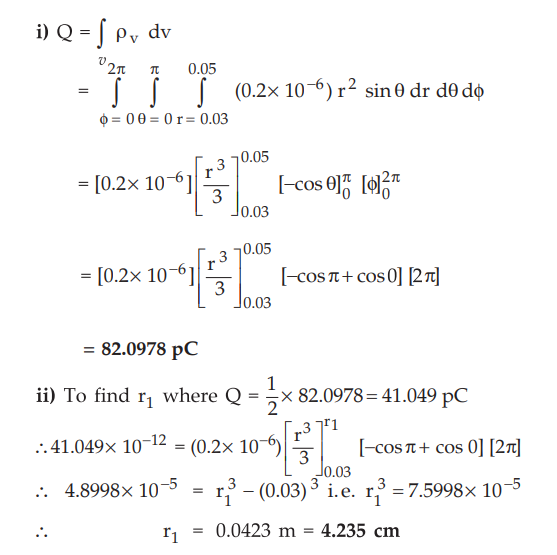
Examples for Practice

Ex. 2.4.3 A volume charge density is expressed as ρ_v = 10z² x sin πy. Find the total charge inside the volume (-1 ≤ x ≤ 2), (0 ≤ y ≤ 1), (3 ≤ z ≤ 3.6).

[Ans.: 62.57 C]

Ex. 2.4.4 A sphere of radius 2 cm is having volume charge density of ρ_v given by ρ_v = cos² θ. Find the total charge Q contained in the sphere. 

[Ans.: 11.1701 C]

Review Question

1. Which are the various types of charge distributions ? Explain. State the units of line charge density, surface charge density and volume charge density.