Types of Integral Related to Electromagnetic Theory

Types of Integral Related to Electromagnetic Theory

AU:Dec.11, May-15

• In electromagnetic theory a charge can exist in point form, line form, surface form or volume form. Hence while dealing with the analysis of such charge distributions, the various types of integrals are required. These types are,

1. Line integral 

2. Surface integral

3. Volume integral.

1. Line Integral

• A line can exist as a straight line or it can be a distance travelled along a curve. Thus in general, from mathematical point of view, a line is a curved path in a space.

• Consider a vector field  shown in the Fig. 1.14.1. The curved path shown in the field is p - r. This is called a path of integration and corresponding integral can be defined as,

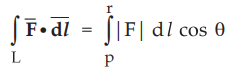 ...(1.14.1)

... Using definition of dot product

 where dl = Elementary length

• This is called line integral of  around the curved path L. It represents an integral of the tangential component of  along the path L. 

• The curved path can be of two types,

i) Open path as p-r shown in the Fig. 1.14.1.

ii) Closed path as p-q-r-s-p shown in the Fig. 1.14.1.

• The closed path is also called a contour. The corresponding integral is called contour integral, closed integral or circular integral mathematically defined as,

• This integral represents circulation of the vector field  around the closed path L.

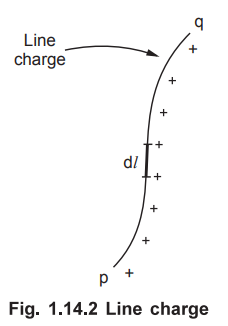
• If there exists a charge along a line as shown in the Fig. 1.14.2, then the total charge is obtained by calculating a line integral.

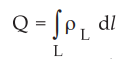... (1.14.3)

where ρ_L - Line charge density i.e. charge per unit length (C/m)

Key Point : In evaluating line integration, the  direction is assumed to be always positive and limits of integration decide the sign of the integral.

2. Surface Integral

• In electromagnetic theory a charge may exist in a distributed form. It may be spreaded over a surface as shown in the Fig. 1.14.3 (a). Similarly a flux may pass through a surface as shown in the Fig. 1.14.3 (b). While doing analysis of such cases an integral is required called surface integral, to be carried out over a surface related to a vector field. For a charge distribution shown in the Fig. 1.14.3 (a), we can write for the total charge existing on the surface as,

where

ρ_S = Surface charge density in C/m²

dS = Elementary surface

• Similarly for the Fig. 1.14.3 (b), the total flux crossing the surface S can be expressed as,

where  = Unit vector normal to the surface S

• Both the equations (1.14.4) and (1.14.5) represent the surface integrals and mathematically it becomes a double integration while solving the problems.

• If the surface is closed, then it defines a volume and corresponding surface integral is given by,

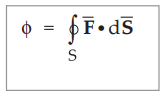.. (1.14.6)

• This represents the net outward flux of vector field  from surface S.

Key Point : 1. The closed surface defines a volume. 2. The surface integral involves the double integration procedure mathematically.

3. Volume Integral

• If the charge distribution exists in a three dimensional volume form as shown in the Fig. 1.14.4 then a volume integral is required to calculate the total charge.

• Thus if ρ_v is the volume charge density over a volume v then the volume integral is defined as,

=...(1.14.7)

Where dv = Elementary volume

Ex. 1.14.1 Show that over the closed surface of a sphere of radius b  = 0 AU : May-15, Marks 6

Ans. :

The sphere is shown in the Fig. 1.14.5. The radius is b ans unit vector normal ti the surface is   .

But   varies with both θ and ϕ hence it is necessary to express unit vector   in rectangular co-ordinate system. Refering section 1.13.4,

Review Question

1. Explain in detail line, surface and volume integrals of vector functions. AU : Dec.-11, Marks 16