Uniform distribution (or) Rectangular Distribution: Example Solved Problems

Example 1.10.1

Electric trains on a certain line run every half an hour between mid-night and six in the morning. What is the probability that a man entering the station at a random time during this period will have to wait atleast twenty minutes ? [A.U. A/M 2008]

Solution :

Let the random variable X denote the waiting time in minutes for the next train.

Given that a man arrives at the station at random

→ X is distributed uniformly on (0, 30) with density

f(x) = 1/30' 0 < x < 30

= 0, otherwise

Thus the probability that he has to wait for atleast 20 minutes is

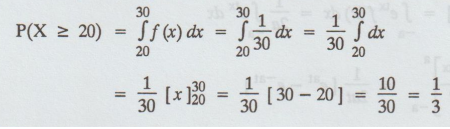
Example 1.10.2

If the random variable X follows uniform distribution in (0, 1) with density f(x) = 1, 0 < x < 1

= 0, otherwise

find the density function of -2 log X.

Solution:

Let Y = -2 log X. Thus the distribution function of Y is

G(y) = P[Y ≤ y] = P[-2 log X ≤ y]

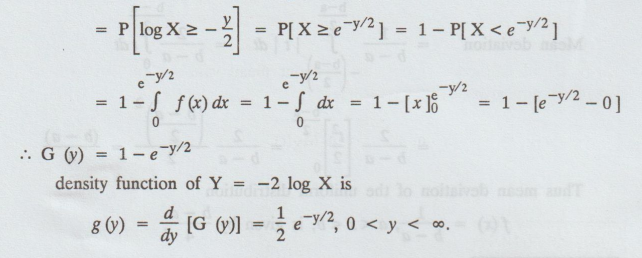
( as X ranges in (0, 1), Y = -2 log X ranges from 0 to ∞) max

Example 1.10.3

Show that for the uniform distribution :

f(x) = 1/2a, -a < x < a

= 0, elsewhere

[A.U. N/D 2006]

the moment generating function about the origin is 1 / a t Also, moments

of even order are given by μ2n = a2n / (2n+1)*

Solution:

Moment generating function about origin is given by

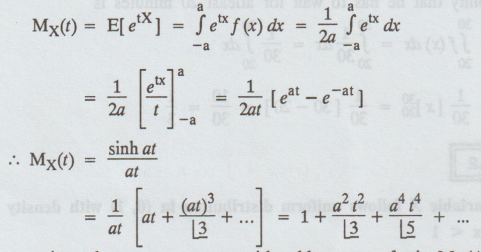
since there are no terms with odd powers of t in Mx(t) all moments of odd order about origin vanish.

(i.e.,) μ2n 2n + 1 = 0

In particular μ = 0 → mean = 0

Thus μ2n = μ2n (mean = 0)

μ2n+1 0, n = 0, 1, 2, …

(i.e.,) all moments of odd order about mean vanish. The moments of even order are given by

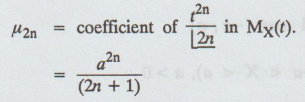
Example 1.10.4

If X is uniformly distributed over (0, 5), find the probability that

(a) X < 2 (b) X > 3 (c) 2 < x < 5.

Solution :

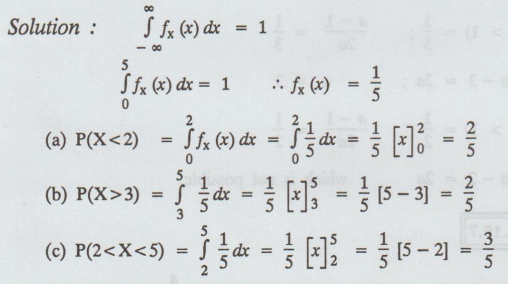
Example 1.10.5

A random variable Y is defined as cos лx where X has a uniform p.d.f. over (-1 / 2 , 1 / 2 ) find mean and standard deviation.

Solution :

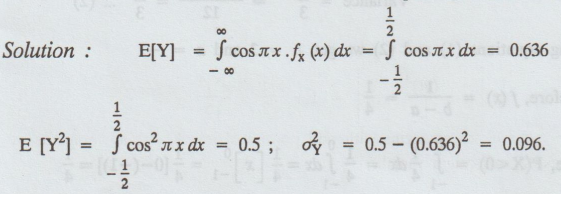
Example 1.10.6

If X is uniformly distributed over (-a, a), a > 0 find a, so as to satisfy the following: (a) P(X ≥ 1) = 1/3  (b) P(X > 1) =  1/2

Solution :

X is uniformly distributed over (-a, a)

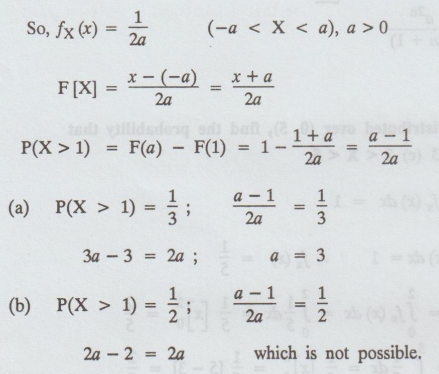
Example 1.10.7

X is uniformly distributed with mean 1 and variance 4/3' find P(X < 0).

[A.U Tvli M/J 2010, CBT A/M 2011]

Solution :

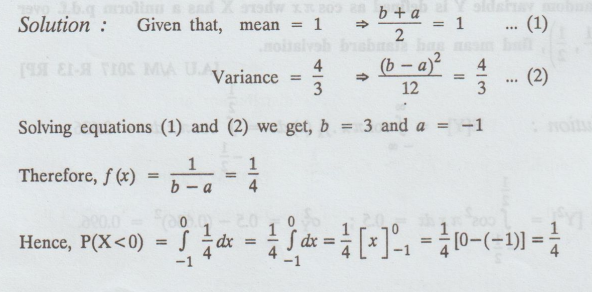
Example 1.10.8

Buses arrive at a specified bus stop at 15 minutes intervals starting at 7 a.m. that is 7 a.m., 7.15 a.m., 7.30 a.m., etc. If a passenger arrives at the bus stop at a random time which is uniformly distributed between 7 and 7.30 a.m. find the probability that he waits (a) less than 5 minutes (b) atleast 12 minutes for a bus.

Solution: Let X denotes the time that a passenger arrives between 7 and 7.30 a.m.

Then X ~ U(0, 30)

Then f(x) = 1 / b – a = 1 / 30 – 0 = 1 / 30

 (a) Passenger waits less than 5 minutes, (i.e.,) he arrives between 7.10 - 7.15 or 7.25 -7.30

P(Waiting time less than 5 minutes)

= P(10 ≤  x  ≤  15) + P(25 ≤ x ≤ 30)

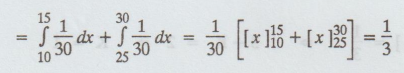
 (b) Passenger waits atleast 12 minutes, (i.e.,) he arrives between

7- 7.03 or 7.15 - 7.18.

P(Waiting time atleast 12 minutes)

= P(0 ≤ x ≤ 3) + P(15 ≤ x ≤ 18)

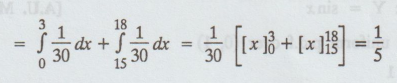
Example 1.10.9

A random variable 'X' has a uniform distribution over (-3, 3) compute

(i) P(X < 2), P(|X| < 2), P(x-2 < 2),

(ii) Find K for which P(X > K) = 1 / 3

 [A.U M/J 2009, CBT A/M 2011]

Solution:

We know that the p.d.f. of a random variable 'X' which is distributed uniformly in (-a, a) is

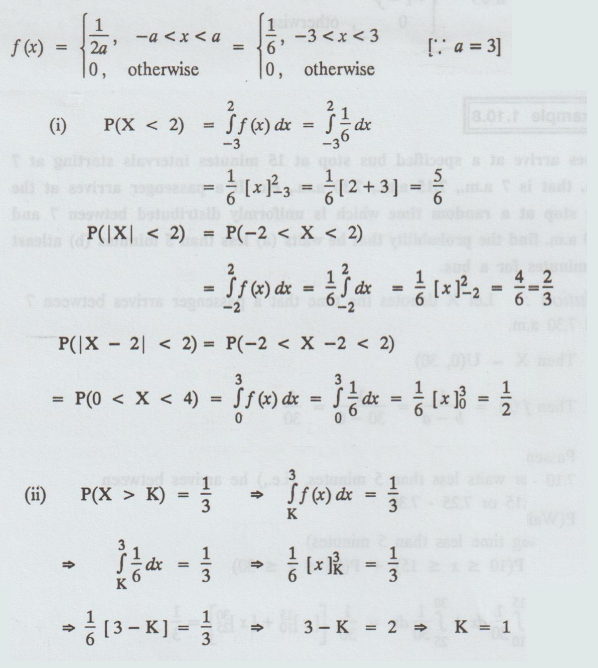
Example 1.10.10

If X is a random variable uniformly distributed in (0, 1), find the pdf of Y = sin x. Also find the mean and variance of Y.

Solution: Given: Y = sinx

X has a uniform p.d.f over (0, 1)

g(y) = 1

G (y) = P(Y ≤ y) P(sinX ≤ y) = P(X ≤ sin-1 y)

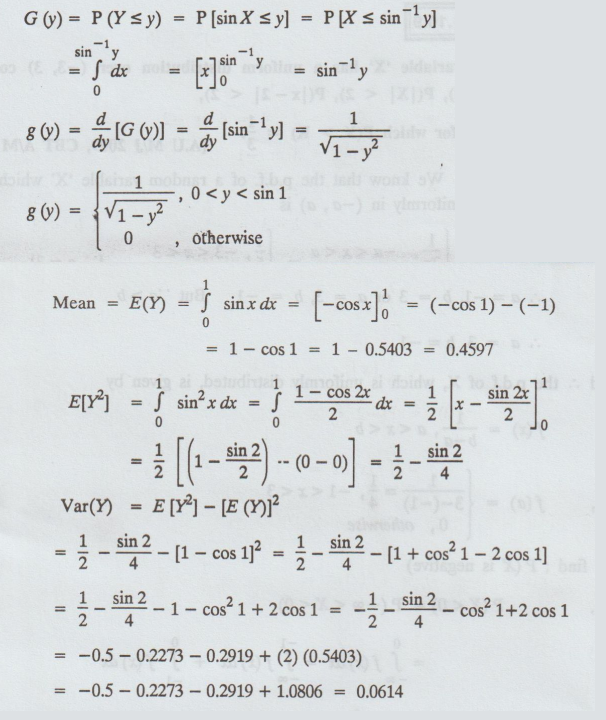
Example 1.10.11

X is uniformly distributed random variable with mean 1 and variance 4/3 If 3 independent observations of X are made, what is the probability that all of them are negative. [A.U A/M 2015 (RP) R8]

Solution:

Let X ~U (a, b)

Mean = a + b / 2, variance = (b - a)2 / 12

Given: a + b / 2 = 1 → a + b = 2 ... (1)

Given: (b - a) 2 / 12 = 4/3 → (b - a)2 = 16

→ (b − a) = ± 4 … (2)

Example 1.10.12

The variates 'a' and 'b' are independently and uniformly distributed in the interval (0, 6) and (0, 9) respectively. Find the probability that the equation x2- ax + b = 0 has two real roots.

Solution :

Example 1.10.13

Starting at 5.00 a.m. every half hour there is a flight from San Francisco airport to Los Angeles International Airport. Suppose that none of these planes is completely sold out and that they always have room for passengers. A person who wants to fly to L.A. arrives at the airport at a random time between 8.45 a.m and 9.45 a.m. Find the probability that she waits (1) atmost 10 mins. (2) atleast 15 mins. [A.U M/J 2007]

Solution: Let X be the uniform r.v. over the interval (0, 60)

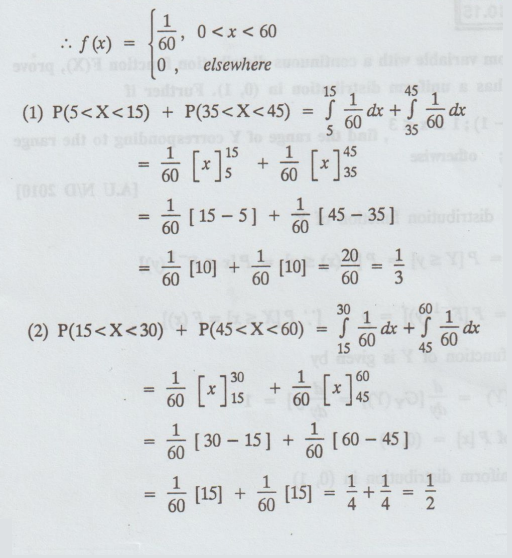
Example 1.10.14

Show that for the uniform distribution f (x) = 1/ 2a', - ɑ < x < ɑ the moment generating function about origin is sinh ɑt / ɑt [AU N/D 2006]

Solution:

Given: f(x) = 1/2 ɑ - ɑ < x < ɑ

To prove : Mx (t) sinh ɑ t / ɑ t

Proof: We know that the moment generating function is

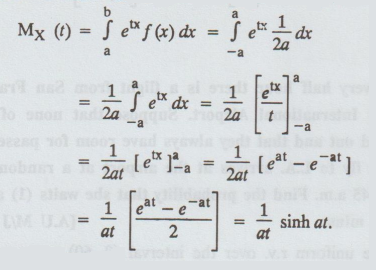
Example 1.10.15

If X is a random variable with a continuous distribution function F(X), prove that Y=F(X) has a uniform distribution in (0, 1). Further if