Uniform distribution (or) Rectangular Distribution

Uniform distribution (or) Rectangular Distribution

1. Uniform Distribution

A random variable X is said to have a continuous uniform distribution over an interval (a, b) if its probability density function is a constant = k, over the entire range of X.

(i.e.,) f(x) = K, a < x < b

= 0, otherwise

Since, the total probability is always unity.

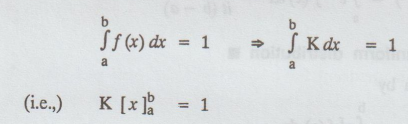
K [b-a] =  1

K =1/ b - a

f(x) = 1/b – a, a < x < b

= 0, otherwise

a and b are said to be the two parameters of the uniform distribution on (a, b).

Note: The uniform distribution is also known as rectangular distribution, since the curve y = f(x) describes a rectangle over the x-axis, between the ordinates x = a and x = b.

2. The distribution function of the uniform distribution

The distribution function F (x) is given by

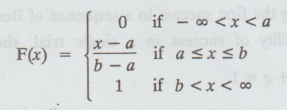
Since F(x) is not continuous at x = a and x = b, it is not differentiable at these points.

Thus d/dx [F(x)] = f(x) = 1 / b – a ≠ 0 exists

everywhere except at x = a and x = b.

Note: The pdf of a uniform variable 'X' in (-a, a) is given by

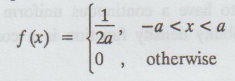
3. Characteristic function of a uniform distribution

Characteristic function is given by

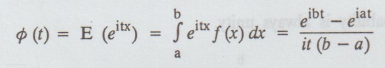
4. Moments of a uniform distribution

Moments are given by

5. Mean deviation about the mean of uniform distribution

Mean distribution about mean is given by