Uniform Plane Electromagnetic Waves in Good Conductor

Uniform Plane Waves in Good Conductor

• A practical or good conductor is the material which has very high conductivity. In general, the conductivity is of the order of 10⁷ Ʊ/m in the good conductors like copper, aluminium etc.

• For good conductors,

σ / ωƐ >> 1

• The propagation constant ɤ is given by,

ɤ = √jωµ (σ + jωƐ)

• As σ >> ωƐ we can neglect imaginary part (jωƐ),

Thus for good conductor,

• For good conductor, ɑ and β are equal and both are directly proportional to the square root of frequency (f) and conductivity (σ).

• The intrinsic impedance of a good conductor is given by,

• But for good conductor, σ >> jωƐ,

• The angle of intrinsic impedance is 45°. As we have already studied that for perfect dielectric i.e. zero conductivity, the intrinsic impedance angle is zero and for the good conductor angle is 45°. Moreover the intrinsic impedance has only a positive angle. This clearly indicates that the field may lag the field  by at the mo st 45°.

• Consider only the component of the electric field E_x travelling in positive z-direction. When it travels in good conductor, the conductivity is very high and attenuation constant ɑ is also high. Thus we can write such a component in phasor form as

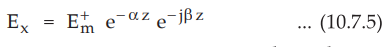
• When such a wave propagates in good conductor, there is a large attenuation of the amplitude as shown in the Fig. 10.7.1.

 

• At z = 0, amplitude of the component E_x is  E_m while at z = d, amplitude is Em e^-ɑd.  z = d, the amplitude gets reduced by the factor e^-ɑd. If we select d = 1/ɑ, then the factor becomes e ^-1 = 0.368. So over a distance d = 1/ɑ the amplitude of the wave decreases to approximately 37 % of its original value. The distance through which the amplitude of the travelling wave decreases to 37 % of the original amplitude is called skin depth or depth of penetration. It is denoted by δ.

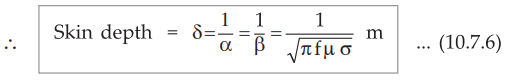
• From the expression of the skin depth, it is clear that 8 is inversely proportional to the square root of frequency. So for the frequencies in the microwave range, the skin depth or depth of penetration is very small for good conductors. And all the fields and currents may be considered as confined to a very thin layer near the surface of the conductor. This thin layer is nothing but the skin of the conductor, hence this effect is called skin effect.

The exponential decay in the amplitude of  field component entering in a good conductor is as shown in the Fig. 10.7.2.

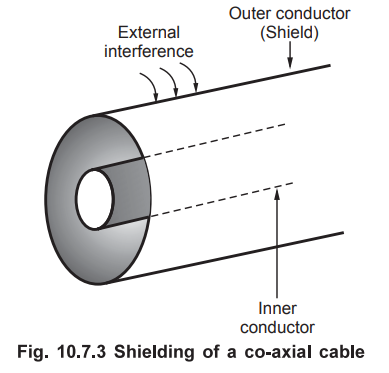
• From above plot, it is clear that in 18 distance, amplitude reduces to 37 % of its original value. For a good conductor, amplitude reduces to almost zero within 2 δ or 3 δ distance. Thus uniform plane wave cannot travel large distance through good conductor. This concept is used in a shielding of a conductor. In a co-axial cable, the inner conductor carries the signal while the outer is shield which is made up of a material having properties of good conductor. So even if there is an external interference, its amplitude reduces to zero within a very short distance due to the outer conductor. Hence the signal carried by inner conductor is not interfered by an external interference.

• The intrinsic impedance of a good conductor interms of skin depth δ is given by,

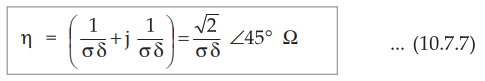
• The velocity of propagation is given by,

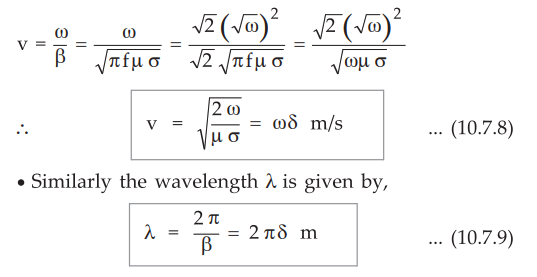
• Equations (10.7.8) and (10.7.9) gives the velocity of propagation and wavelength expressed interms of skin depth δ( as β = 1/δ).

 

Ex. 10.7.1 A uniform plane wave is travelling at a velocity of 2.5 × 10⁵ m/s having wavelength λ = 0.25 mm in a non-magnetic good conductor. Calculate the frequency of wave and the conductivity of a medium.

Sol. : The velocity of propagation is given by,

 

Ex. 10.7.2 Calculate intrinsic impedance ɳ, the propagation constant ɤ and wave velocity v for a conducting medium in which σ = 58 MS/m, µr = 1, Ɛr = 1 at a frequency of 100 MHz.

Sol. : For conducting medium, σ = 58 MS/m. So using expressions of η, ɤ and v for good conductor. The intrinsic impedance is given by,

 

Ex. 10.7.3 The current density at the surface of a thick metal plate is 100 A/ m². What is the skin depth if the current density at a depth of 0.01 cm is 28 A/ m² ?

AU : May-10, Marks 4

Sol. : Current density  at surface = 100 A/ m²

Current density at 0.01 cm = 28 A/ m²

Depth from surface = 0.01 cm = 0.01 × 10^-2 m

Now current density in a conductor is given by,

where  (z) is an electric field in conductor. In general, an electric field in conductor is given by,

 

Ex. 10.7.4 Calculate skin depth for medium with conductivity 100 Ʊ/m, relative permeability 2, relative permittivity 3 at 50 Hz, 1 MHz and 1 GHz.

AU : May-08, Marks 8

Sol. : By definition, skin depth is given by,

Ex. 10.7.5 Calculate the skin depth and wave velocity at 2 MHz in aluminium with conductivity 40 MS/m and μ, =1

AU Dec.-05, Marks 6

Sol. : For aluminium with very high conductivity, the propagation constant is given by,

 

Ex. 10.7.6 The depth of penetration in a certain conducting medium is 0.1 m and the frequency of the electromagnetic wave is 1.0 MHz. Find the conductivity of the conducting medium.

Sol. : For conducting medium, assume µ_r = 1. The depth of penetration is given by,

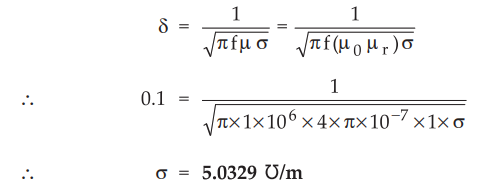
σ = 5.0329 Ʊ/m

 

Ex. 10.7.7 A metal sheet of Aluminium has V = 38.2 M Ʊ/m and µ_r = 1. Calculate the skin depth δ the propagation constant ɤ and velocity of propagation v at the frequency of 1.6 MHz.

Sol. : For a given metal i.e. aluminium, σ = 38.2 MS/m which is very high. Thus it can be used as good conductor material. For good conductor, the propagation constant is given by,

 

Examples for Practice

Ex. 10.7.8 A uniform plane wave propagating in a medium has

If a medium is characterized by Ɛr = 1 µr = 20 and σ = 3 S/m, determine ɑ, β and .

Ex. 10.7.9 Determine ɑ, β, ɤ, v, η  for damp soil at a frequency of 1 MHz given that

Ɛ_r =12, µ_r =1 and σ = 20 mS/m.

[Ans.: 0.2809 Np/m, 0.2809 rad/m, 22.36 × 10⁶ m/s, 22.368 m, ∠ 44.05° Ω]

Ex. 10.7.10 Determine the depth of penetration for copper at 1 MHz.

[Ans.: 66.085 hm]

Review Questions

1. Derive the expressions describing propagation of uniform plane wave in good conductor.

AU : Dec.-16, May-18, Marks 7

2. Define skin depth and state its effect.

AU : Dec.-08, Marks 6

3. Explain the propagation of EM wave inside a conductor.

4. Define skin depth.

5. Calculate the skin depth of copper at 60 Hz and at

6 GHz.       

[Ans.: 8.53 × 10^-3m, 8.53 x 10^-7 m]

6. Derive expression for an intrinsic impedance, propagation constant and velocity of a wave in conducting media and good conductor.

AU : May-14, Marks 8