Uniform Plane Waves in Free Space

Uniform Plane Waves in Free Space

Dec.-05, 06, 08, 12, 16, 17, May-16, 17, 18

• Consider an electromagnetic wave propagating through the free space. For free space, σ = 0. Consider that the electric field in the wave is in x-direction only while the magnetic field is in y-direction only. Both the fields, i.e. electric field and magnetic field do not vary with x and y but vary only with z. The fields also vary with time as wave propagates in the free space.

• Basically plane waves means, the electric field vector    and the magnetic field vector  lie in the same plane. Also the different planes along the direction consisting  and  vectors are parallel to each other along the direction of propagation of wave. The uniform plane wave means the  and  field vector are in same plane. Moreover the amplitude and phase of field vectors  and  is constant over the planes parallel to each other. A uniform plane with field vectors  and  is illustrated in the Fig. 10.3.1 (a) and (b).

• Electric field vector is in direction while magnetic field is in  direction. That means 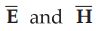 lie in x-y plane. So in any of the planes in the wave, the vectors 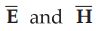are independent of x and y. Thus we can conclude that 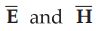are function of z and t only. Moreover as 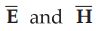 are mutually perpendicular to each other, the electromagnetic waves are also called transverse electromagnetic waves. As the wave travels in the z-direction. It is clear that direction of the electromagnetic wave i.e. uniform plane wave is perpendicular or orthogonal to the plane consisting the 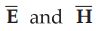 field vectors.

• Let us consider wave equations for the 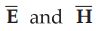 fields given by,

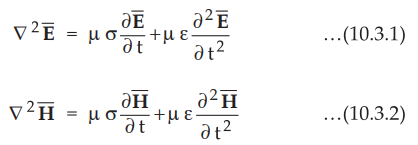
• But for free space, σ = 0 and ε = ε₀, µ = µ₀ substituting these values in equations (10.3.1) and (10.3.2), the wave equations are modified as,

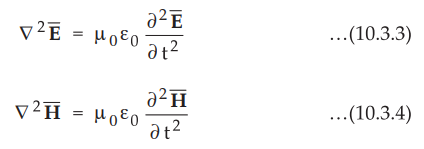
Consider equation (10.3.3), we can write,

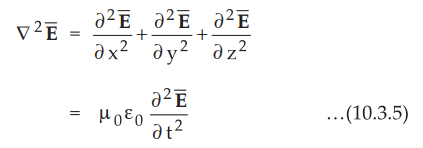
• But the wave travels in the z-direction, hence   is independent of x and y. Hence first two differential terms in above equation are zero. Hence we can write,

• Modifying equation (10.3.6) by rearranging terms, we get,

• Now according to the results in physics,

where c = 3×10⁸ m/s = Velocity of light

 • Substituting in equation (10.3.7), we get,

• Above equation is other form of the wave equations. Similar to this we can also write,

• Let us consider equation (10.3.6), given as,

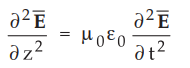
• For the wave propagating in z-direction,   may have E_x and E_y component but definitely not E_z. According to assumption, direction, so let us consider that only E_x is present. Then we can rewrite above equation as,     

∂²E_x/ ∂z² = µ₀ ε₀ ∂²E_x / ∂t² .......(10.3.10)

Let     E_x = E_m e^jωt

Where         E_m = Amplitude of the electric field

ω = Angular frequency

• Partially differentiating E_x twice with respect to t, we get,

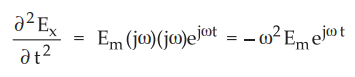
But E_m e_jωt = E_x, thus we can write,

∂²E_x/∂t² = - ω²E_x

Substituting in equation (10.3.10), we get,

Thus auxiliary equation becomes, 

(D² + ω²µ₀ε₀)E_X = 0

Hence equating bracket term to zero, we get,

D2 + ω²µ₀ε₀ = 0

or      D² = -ω²µ₀ε₀

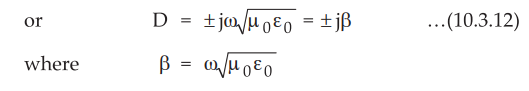
which is called phase shift constant measured in rad/m.               

Hence the solution of equation (10.3.11) can be written as,    

• Let K₁ and K₂ be the constants with respect to z but are functions of t. Let us assume K₁ and K₂ as,

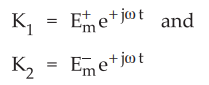
• Substituting values of K₁ and K₂ in equation (10.3.13) we get,

•To find the electric field in the time domain, taking real part of equation (10.3.14), we get,

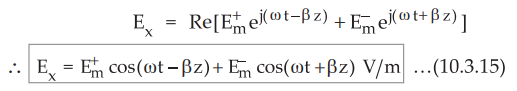
• Above equation (10.3.15) is the sinusoidal function consisting two components of an electric field; one in forward direction and other in backward direction. The wave thus consists one component of the field travelling in positive z-direction having amplitude E⁺_m; while other component of the field travelling in negative z-direction having amplitude E^-_m.

• The equation for H_y can be obtained in the similar way by simplifying equation (10.3.4) and the equation is given by,

 • This equation is very much similar to equation (10.3.15) representing two components of a magnetic field, one in forward direction, while other in backward direction.

• Thus from equations (10.3.15) and (10.3.16) it is clear that   is in x-direction while  is in y-direction. Both   and  are in time phase and are mutually perpendicular to each other. Both these fields lie in the plane which is mutually perpendicular to the direction of wave propagation. Thus   and  together form transverse electromagnetic wave (TEM wave). Thus   and  are only functions of time and direction of travel.

 

1. Phase Velocity(v_p)

• The phase velocity of the uniform plane waves is defined as the velocity with which the phase of the wave propagates. It is denoted by v_p or simply v. In other words, the phase velocity indicates the progression of z co-ordinate in the argument of cosine function i.e. cos (ω_t - βz).

Thus phase velocity is given by,

v = v_p = dz/dt = ω/β

But β = ω√µε in general.

v = 1/√µβε₀ = v_p .......(10.3.17)

• Above equation (10.3.17) is the general equation for the phase velocity of the uniform plane wave. We can rewrite equation (10.3.17) as,

For free space, µ = µ₀ and ε = ε₀

v = 1/ √µ₀ ε₀ where µ₀ = 4π × 10^-7 H/m,

ε₀ = 8.854 × 10^-12 F/m

• Substituting values of µ₀ and ε₀, the velocity of the uniform plane wave in free space is given by,

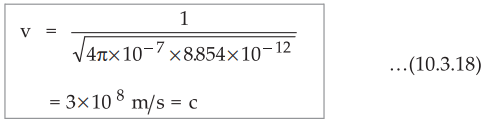
= 3 × l0⁸m/s = c 

where          c = Velocity of light in free space

= 3×10⁸ m/s

• Thus in free space (σ = 0, µ = µ₀, ε = ε₀), the uniform plane waves travel with the velocity of light i.e. 3 × 10⁸ m/s.

i) Group Velocity (v_g)

• The velocity of entire group of waves as a whole is called group velocity denoted as V_g.

• The phase velocity is the velocity with which phase of the wave propagates denoted as v_p. The phase velocity V_p of waves is generally larger than the group velocity V_g.

• The relation between v_p and v_g is given by,

v_g = dω/dβ = v_p – λ dv_p/dλ

• If the phase velocity is not dependent on the wavelength λ of the propagative wave then dv_p/dλ = 0 and v_g = v_p. Such a medium is called non-dispersive medium.

• The medium in which v_g < v_p is called normal dispersion while medium in which v_g > v_p is called anomolous dispersive medium.

• The sound waves is a good example of non-dispersive medium where all the individual waves which make up the sound wave as a whole travel at same speed and hence v_p = v_g.

• Thus the group velocity is the velocity with which the entire group of waves travel.

 

2. Relationship between 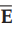    and 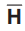 in Free Space - Concept of Intrinsic Impedance (η)

• In general, an electromagnetic wave in any medium can be defined completely if the properties of the medium such as intrinsic impedance  (η), propagation constant (ɤ) are known.

• Consider Maxwell's equation derived from Faraday's law,

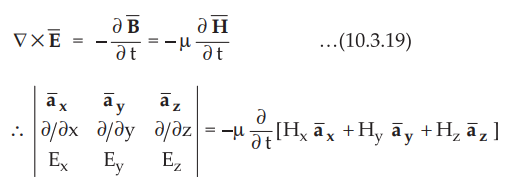
Assume that uniform plane wave is propagating in z-direction. Thus above equation gets modified as,

Also assume that the electric field and magnetic field are mutually perpendicular to each other and the direction of propagation. Then Ey = 0 and H* = 0. Thus above equation gets simplified as,

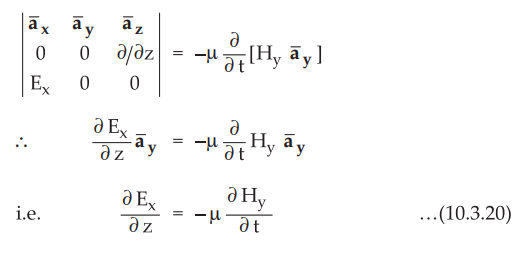
But from equation (10.3.15),

Differentiating with respect to z, we get,

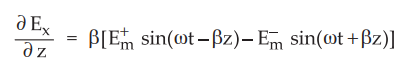
Substituting ∂E_x/ ∂z in equation (10.3.20) we get,

Comparing equation (10.3.22) with equation (10.3.16), we get,

• Equations (10.3.23) and (10.3.24) are analogous to the Ohm's law i.e. I = V/Z where, I and V are analogous to H and E. Thus the radical term is nothing but the impedance with unit ohm. Such impedance is expressed interms of µ and e which are properties of the medium. Hence the impedance is called intrinsic impedance of the medium and is denoted by η.

• Hence in general,

• But for free space,

µ = µ₀ = 4π × 10^-7 H/m , ε = ε₀ = 8.854 × 10^-12 F/m

• Hence for free space, the intrinsic impedance is denoted by η₀ and is given by,

 • From equation (10.3.26) it is clear that for free space η₀ is purely resistive. The general expression for η interms of η₀ is given as,

 

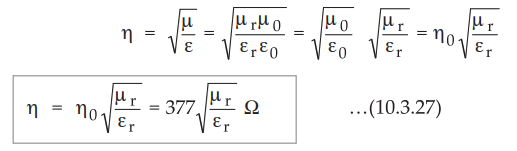
3. Propagation Constant (ppppp)

• Consider Maxwell's equation derived from Faraday's law given by,

Taking curl on both the sides,

• Using vector identity on L.H.S. and interchanging operations on R.H.S., we get equation same as equation (10.2.10) that derived in section 10.2. Using the simplified equation (10.2.10) we can write,

• In uniform plane waves, both  and  vary with time. So by property of phasors, when the fields vary with respect to time, then the partial derivative with respect to time can be replaced by jm Rewriting above equation in phasor form, we get,

• Equations (10.3.28) and (10.3.29) are called wave equations in phasor form. In equations (10.3.28) and (10.3.29), the term inside the bracket is same. This term represents the properties of the medium through which the wave is travelling. It is square of the propagation constant (ɤ). Hence wave equations can be rewritten as,

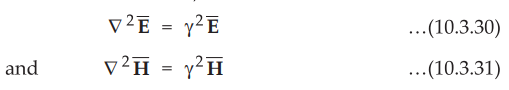
• Hence, in general, the propagation constant can be expressed interms of the properties of the medium as,

• But the propagation constant y is the complex quantity made up of real and imaginary term. Thus

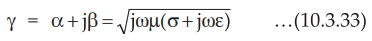
• In general, when wave travels through medium it gets attenuated. That means the amplitude of the medium reduces. It is represented by the real part of the propagation constant. It is called attenuation constant (∝). It is measured in neper per metre (Np/m). But practically a is expressed in decibel (dB). The relation between the basic unit neper and practical unit decibel is given by,

1 Np = 8.686 dB

Or

1 dB = 0.115 Np

• The real part of the propagation constant i.e. ∝ is given by,

• Similarly when a wave travels through the medium, phase change occurs. Such a phase change is expressed by an imaginary part of the propagation constant. It is called phase shift constant or simply phase constant (β). It is measured in radian per metre (rad/m). Thus imaginary part of the propagation constant i.e. β is given by,

• From the phasor form of the wave equation, the intrinsic impedance of the medium in general is given by,

Now for free space, σ = 0, ε = ε₀ and μ = μ₀, then,

Hence for free space,

σ = 0

β = ω√μ₀ε₀ ............ (10.3.37)

• Thus for free space, the propagation constant is purely imaginary.

 

4. Wavelength (λ)

• In general, the wave repeats itself after 2π radian. Thus the distance that must be travelled by the wave to change phase by 2π radian is called wavelength and is denoted by λ

Wavelength = λ = 2π/β m...(10.3.38)

Putting        β = ω√με we get,

But ω/2π = f in Hz and 1/√με = v

λ = v/f m .......................(10.3.39)

• Hence velocity can also be expressed as,

v = λ f m/s...(10.3.40)

• For free space,

λ = v₀/f = c/f ...(10.3.41)

• Let us summarize the equations describing the propagation of electromagnetic waves in any medium in general.

• Let us now summarize the equations which will help is describing propagation of uniform plane waves (or EM waves) in free space as medium.

• For free space, σ = 0, μ = μ₀, ε = ε₀

Ex. 10.3.1 A uniform plane wave 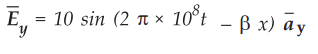is travelling in x-direction in free space. Find i) Phase constant, ii) Phase velocity and iii) Expression for 

Sol. : A wave travelling in x-direction with the electric field in y-direction can be expressed as,

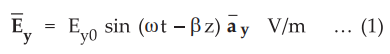
where E_y0 is the magnitude of the electric field in y-direction.

By comparing the given expression of  with equation (1), we can write,

ω = 2π × 10⁸ rad/sec. and E_y0 = 10 V/m

For free space ε_r = 1 = μ_r. For a uniform plane wave in free space, v = ω/β

In free space, v = c = 3 × 10⁸ m/sec. Hence phase constant is given by,

β = ω/v = 2 × π × 10⁸/3 × 10⁸ =  2.09435 rad/m

For free space, the intrinsic impedance is given by,

η₀ = 120 π = 377 Ω

The magnitude of the magnetic field is given by,

H_z0 = E_y0/ η₀ = 10/377= 0.026525 A/m

= 26.5251 mA/m

As wave is trvelling in positive x-direction and the electric field is in y-direction, the magnetic field must be in positive z-direction. Hence the magnetic field expression can be given as,

Substituting the values of H_y0, ω and β we can write,

 

Ex. 10.3.2 A uniform plane wave has a wavelength of 2 cm in free space and 1 cm in a perfect dielectric (σ=0, μ_r = 1). Determine the relative permittivity of the dielectric.

Sol. : In free space, the velocity of propagation is given by,

v₁= c = 3 × 10⁸ m/s

The wavelength in medium 1 i.e. free space is related with frequency given by the expression,

λ₁ = c/f

Hence the frequency is given by,

f = c/λ₁ = 3 × 10⁸/ 2 × 10^-2 = 15 × 10⁹ Hx

= 15 GHz

Now the same wave travels in perfect dielectric medium, with wavelength λ₂ =1 cm =1×10⁻² Even if the wave travels in another medium, frequency f remains same. Hence the velocity of wave in the perfect dielectric is given by,

v₂ = fλ₂ = (15×10⁹) (1×10^-2)=1.5×10⁸ m/s

For the perfect dielectric, the velocity of the wave can be expressed as,

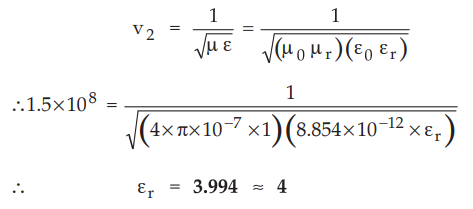
Hence the relative permittivity of the dielectric is ε_r = 4.

 

Ex. 10.3.3 An     field in free space is given as 

Find i) β, ii) λ, iii)     at P (0.1, 1.5, 0.4) at t = 8 nsec.

Sol. :

i) For uniform plane wave in free space,

β = ω/c = 10⁸ / 3 × 10⁸ = 0.3333 rad/m

ii)

λ = 2π/ β = 2π / 0.3333 = 18.85 m

iii) The magnetic field intensity in the free space is given by,

For free space, η₀= 120π=377Ω.  Since power flow is in y-direction and  is in z-direction, the direction of  will be + x-direction.

 

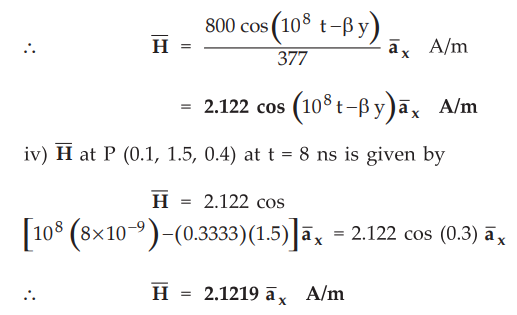
Ex. 10.3.4 A uniform plane wave in air has, 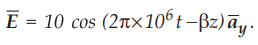 Calculate β and λ.

Sol. : The standard form of an electric field intensity is given by

 = E_m cos (ωt - βz)

Comparing, we can write,

ω = 2π × 10⁶ rad/sec      i.e.

2πf = 2π × 10⁶ i.e. f = 10⁶ Hz

Now wavelength is given by

λ = v/f = c/f

As uniform plane wave propagates in air i.e. free space, the velocity of wave equals to that of light in free space i.e. c = 3 × 10⁸ m/sec

λ = 3 × 10⁸/10⁶ = 300m

But β =2π/λ= 2 × 3.142/300 = 0.0209 rad/m

 

Ex. 10.3.5 If a wave with 100 MHz frequency propagates in free space find propagation constant.

Sol. : Given : f =100 MHz = 100 × 10⁶ Hz

Medium is free space. Hence µ = µ₀ and ε = ε₀

By definition, the propagation constant of a wave in a free space is given by,

But for free space, σ = 0. Hence the expression for ɤ can be written as,

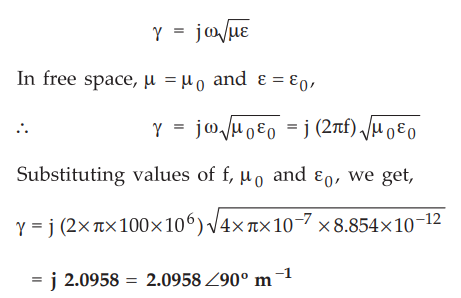
= j 2.0958 = 2.0958 ∠ 90° m^-1

 

Ex. 10.3.6 The electric field intensity associated with a plane wave travelling in a perfect dielectric medium is given by E_x(z,t) = 10cos(2π × l0⁷t - 0.1 πz) V/m. What is the velocity of propagation ?AU : May-18, Marks 6

Sol. : Comparing the equation with standard equation,

E_z(z,t) = E_mcos(ωt- βz)

ω = 2π × 10⁷ rad/sec, β = 0.1 K rad/m

Thus the velocity of propagation is,

v = ω/β = 2π × 10⁷/0.1π = 2 × 10⁸ m/s

Examples for Practice

Ex. 10.3.7 The electric field in free space is given by 

i) Find the direction of wave propagation

ii) Calculate β and the time it takes to travel a distance of λ / 2

Hi) Sketch the wave at t = 0, T/4 and T/2.

Ex. 10.3.8 The magnetic field intensify of uniform plane wave in air is 20 A/m along    direction. 

The wave is propagating in z-direction at a frequency of 2 × 10⁹ rad/sec. Find

a) Wavelength b) Frequency f c) Period d) Amplitude of  .

[Ans. : 0.9424 m, 0.3183 GHz, 7540 V/m]

Ex. 10.3.9 A 10 GHz plane wave travelling in a free space has an amplitude of   as E_x = 10V/m. Find β, ɳ, v, λ and amplitude, direction of  .

[Ans. 209.58 rad/m, 2.9979 × 10⁸ m/s, 0.03 m, 0.0265 A/m]

Review Questions

1. Define propagation constant, attenuation constant, phase constant, intrinsic impedance. For free space what are the values of intrinsic impedance and velocity of propagation?

2. Discuss group velocity, phase velocity and propagation constant of electromagnetic waves.

AU May-16, Marks 8

3. Derive the electromagnetic wave equation (in frequency domain) and the propagation constant and intrinsic impedance.

AU: Dec.-06, 08, Marks 8

4. Derive the electromagnetic wave equations in free space and mention the types of solutions.

AU: Dec.-05, 12, 17, May-17, 18, Marks 10

5. Prove that the intrinsic impedance offered by free space is 120 лΩ.