Uniform Plane Waves in Lossy Dielectric

Uniform Plane Waves in Lossy Dielectric

• Practically all the dielectric materials exhibit some conductivity (σ ≠ 0). So during analysis of the uniform plane waves through dielectric with some amount of conductivity, we cannot neglect o by assuming it to be zero. Due to certain conductivity, certain amount of loss in the medium takes place. Hence the wave travelling through such medium gets attenuated (σ ≠ 0). Such dielectric is called lossy dielectric. The results obtained for the lossy dielectric are different as compared with the results for perfect dielectric medium.

• Let us consider that a uniform plane wave travels in z-direction through the lossy dielectric (σ ≠ 0). The wave equation for the electric field vector  is given by,

• Using vector indentity on L.H.S. of equation (10.6.1), we get,

• Now the wave travels in z-direction, then E is the function of z and t only, hence equation (10.6.2) becomes,

Equation (10.6.8) can be written as,

• Where K₁ and K₂ are constants with respect to z but be the functions of time t.

• Substituting values of K₁ and K₂ in equation (10.6.11), we get,

• Above equation indicates the equation of electric field in the uniform plane wave travelling through lossy dielectric in the z-direction. Assuming that wave travels in +z-direction, the wave equation becomes,

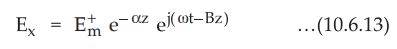
Taking real part of the term on R.H.S., we get,

• Thus from equations (10.6.12), (10.6.13) and (10.6.14), the wave travels in positive z-direction with velocity ω/β m/s. As the wave prograss, it gets attenuated by the factor e^-a. Thus a indicates the rate at which wave is attenuated in amplitude during the propagation through lossy dielectric with some finite non-zero conductivity.

• The propagation constant ɤ in lossy dielectric is given by,

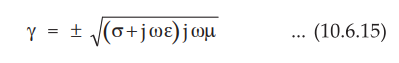
Rearranging the terms,

• From equation (10.6.16), it is clear that the propagation constant for lossy dielectric medium is different than that for lossless dielectric medium, due to the presence of radical factor. When σ becomes zero as in case with perfect dielectric, the radical factor becomes unity and we can obtain the propagation constant ɤ for perfect dielectric. It is also clear from equation (10.6.16) that the attenuation constant a is not zero. By substituting the values of ω, σ,µ and Ɛ, the attenuation constant (ɑ) and phase constant (β) may be calculated. The presence of a indicates certain loss of signal in the medium, hence such medium is called lossy dielectric.

• When a wave propagates in a lossy dielectric, amplitude of the signal decays exponentially due to the factor e^-ɑz. For forward as well as backward waves, the amplitude decays exponentially.

• As σ is not zero, the intrinsic impedance becomes a complex quantity. It is given by,

• Being a complex quantity, h is represented in polar form as shown in above equation. This angle 0n indicates phase difference between the electric and magnetic fields. Thus in lossy dielectric, the electric and magnetic fields are not in time phase.

• The intrinsic impedance can be expressed as,

• This angle depends on the properties of the lossy dielectric medium as well as the frequency of a signal. For low frequency signal, ro becomes very small. Then

θ_n ≈ π/4 rad

• For very high frequency signals,

θ_n ≈ 0

• Thus the range of θ_n for complete frequency range, from 0 to very high frequency is 0 < θ_n < π/4.

 

Ex. 10.6.1 A lossy dielectric is characterized by Ɛ_r = 2.5, µ_r = 4 and σ = 10^-3 Ʊ/m at a frequency 10 MHz. Find, i) Attenuation constant; ii) Phase constant; iii) Velocity of propagation ; iv) Wavelength and v) Intrinsic impedance.

Sol. : For lossy dielectric,

µr =4, Ɛr = 2.5, σ = 10^-3 Ʊ/m, f = 10 MHz

i) The propagation constant is given by,

 

1. Uniform Plane Wave in Practical Dielectric

• As we have already studied, for perfect dielectric conductivity is zero (σ = 0). But for practical dielectric, conductivity is not zero ; but it is very small. The condition for practical dielectric is that the loss in the signal is very small i.e. σ < < jωƐ.

• The propagation constant is given by,

• Consider radical term, Mathematically using binomial theorem,

where |x|  < 1.

• In our case |x|  < 1 and n = 1/2, then neglecting higher order terms, we can write,

• Substituting above value for the radical term,

• Comparing the real terms, the attenuation constant is given by,

• Similarly comparing the imaginary terms, the phase constant is given by,

• In general, the intrinsic impedance ɳ is given by,

• As x = σ /  jωƐ is very small as compared to 1, so neglecting higher order terms,

(1 + x)^-n = 1 - nx

• Using above result, the intrinsic impedance can be written as,

• For practical dielectric material, the conductivity is very small. This indicates that the loss in the signal is very small. Let us obtain the condition which indicates whether the loss is small or not. Consider Maxwell's equation,

• We know that when the fields are time varying the partial derivative with respect to time can be replaced by j ω.

• Thus the ratio of the conduction current density to the displacement current density is given by,

• These two current density vectors point in same direction in space as shown in the Fig. 10.6.1. From the expression of ratio of two current densities, it is clear that displacement current density leads conduction current density by 90°.

• The angle θ by which the displacement current density leads the total current density is given by,

θ = tan^-1 σ / ωƐ

or tan θ = σ / ωƐ

Key Point : The term σ/ωƐ is called loss tangent of dielectric and the angle θ is called loss angle.

• When σ  >> ωƐ, the loss tangent is very high, thus a medium is said to be good conductor. When σ  >> ωƐ, the loss tangent is also small, thus a medium is said to be good dielectric. Hence any medium behaves as a good conductor at low frequencies while exhibits the properties of lossy dielectric at very high frequencies.

 

Ex. 10.6.2 A 9 GHz wave is propagating through a material that has a dielectric constant of 2.4 and loss tangent of 0.005. Find a, β and the wavelength of the material.

Sol. : The loss tangent for a dielectric is given by

For given dielectric σ/jωƐ << 1, thus it is considered to be practical dielectric

For practical dielectric

The propagation constant is given by,

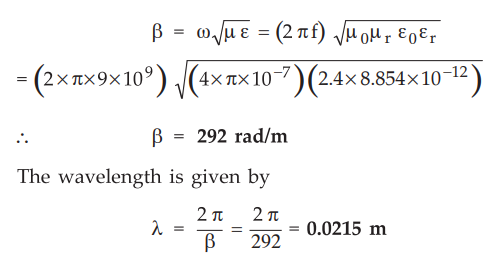
Ex. 10.6.3 A uniform plane wave of has σ = 20 × 10^-3 S/m, Ɛ = 2 Ɛ₀ is and μ = μ₀ having a frequency of 1 MHz.

i) Test the type of material

ii) Calculate the following

1) Attenuation constant

2) Phase constant

3) Propagation constant

4) Intrinsic impedance

5) Wave length

6) Velocity of propagation

AU: Dec.-18, Marks 13

Sol. :

Examples for Practice

Ex. 10.6.4 A lossy dielectric has µr = 1, Ɛr = 50 and σ = 60 Ʊ/m d 15.9 MHz. Find a, 3 v and ’ if the uniform plane wave is travelling through this medium.   

[Ans.: ɳ = 1.4465 ∠ 44.98° Ω

Ex. 10.6.5 Calculate the attenuation constant and phase constant for a uniform plane wave with frequency of 10 GHz in polythelene for which µ = µ0, Ɛr, = 2.3 and σ = 2. 56 × 10-4 Ʊ/m.

[Ans.: ɑ = 0.0554 Np/m and β = 317.84 rad/m]

Review Questions

1. What do you mean by practical dielectric ? What are the values of propagation constant and intrinsic impedance ?

2. Explain the wave propagation in lossy dielectrics.

3. Explain the concept of 'Plane waves in lossy dielectrics.' Deduce the results.

4. Describe the concept of electromagnetic wave propagation in a linear, isotropic, homogeneous, lossy dielectric medium.