Uniform Plane Waves in Perfect (or Lossless) Dielectric

Uniform Plane Waves in Perfect (or Lossless) Dielectric

AU : May-04, 06. 14,18,19, Dec.-ll, 14. 16, 17

• Consider that the uniform plane wave is propagating through a perfect dielectric. If the medium is perfect dielectric, then its properties are given by, σ = 0, μ = μ_r μ₀ and ε = ε_r ε₀. For the perfect dielectric as conductivity is zero (i.e. σ = 0), the medium is also called lossless medium.

• The analysis of the uniform plane waves propagating through the perfect dielectric is very much similar to that for the wave propagating through the free space as in both cases σ = 0. But the expressions are different as the values of permeability and permittivity are different. For the free space, μ = μ₀ and ε = ε_r. Let the values of the permittivity and permeability for the perfect dielectric be ε = ε₀ ε_r and μ = μ₀ μ_r respectively.

• By using the expressions for the different quantities related to the wave propagation as given in Table 10.3.1.

The velocity of propagation is given by,

• The propagation constant is given by,

• For the perfect dielectric, substituting σ = 0, ε = ε₀ ε_r and μ = μ₀ μ_r in above expression we get,

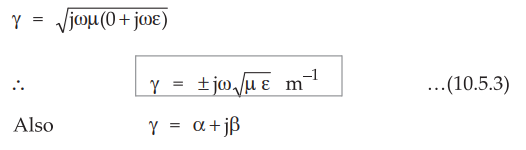
• Hence the attenuation constant for the perfect dielectric is given by,

α = 0 ...(10.5.4)

• The phase constant for the perfect dielectric is given by,

β = ω √ με rad/m .........(10.5.5)

• The intrinsic impedance is given by,

η = √jωμ/ σ √ηωε

• Putting σ = 0 for perfect dielectric, we get,

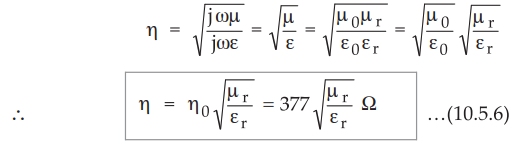
• Summarizing the results for the propagation of wave through perfect dielectric in Table 10.5.1.

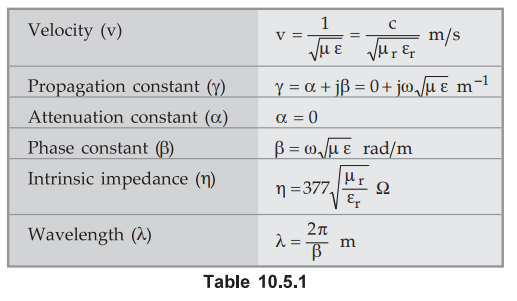
Key Point : As in perfect dielectric, σ = 0 and the attenuation constant is also zero, the perfect dielectric medium is also called lossless dielectric medium.

 

Ex. 10.5.1 An EM propagating in a certain medium is described by, 

i) Determine the direction of wave propagation

ii) Compute the period T, the wavelengh and velocity.

iii) Sketch the wave at t = 0, T/8, T/4 and T/2.

Sol. :

i) From the expression of    , it is clear that the term associated with β is - 6x i.e. - β x. From the basics of wave propagation, the factor 3 is always associated with the term representing direction of propagation. So in above case, the wave propagates in + ve x-direction.

ii) Comparing expression of    with standard expression,

ω = 2π × 10⁶ and β=6, E_m = 25

Now f = ω/2π = 2π × 10⁶/        2π = 10⁶ = 1 MHz

Hence period T is given by,

T = 1/f = 1/10⁶ = 1 µsec

The wavelength is given by,

λ = 2π/β = 2π/6 = 1.0472 m

The velocity is given by,

v = λf = 2 × 1 × 10⁶ = 2 × 10⁶ m/sec

iii) Now T = 1/f  = 2π/ω

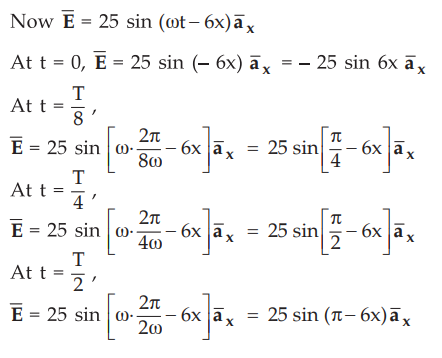
From the Fig. 10.5.1, it is clear that the point P moves along +x direction with velocity v.

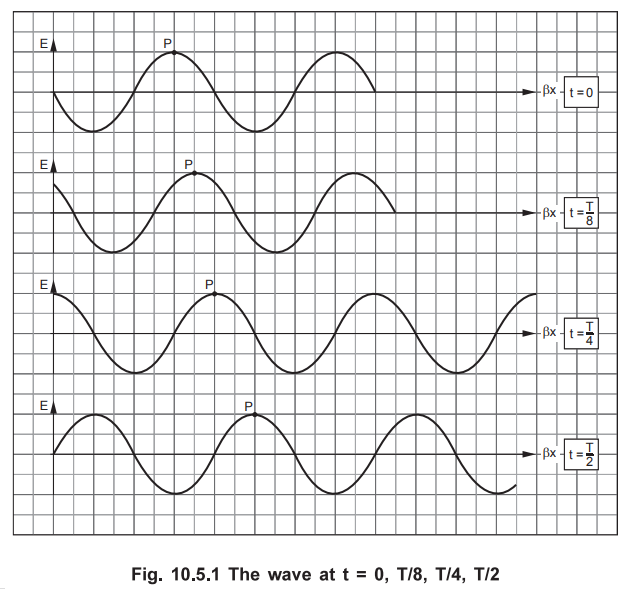
Ex. 10.5.2 Find frequency after which the earth may be considered as perfect dielectric. Assume σ/ωε = 1/100. Given σ = 5 × l0^-3 S/m, μ_r = 10 and ε_r = 8.

Sol. : To find frequency after which the earth may be considered as perfect dielectric, using condition.

σ/ωε ≥ 1/100 as the cut-off

f  ≥ 1.1234 x 10⁹ Hz = 1.1234 GHz

Hence after 1.1234 GHz, the earth may be considered as perfect dielectric.

 

Ex. 10.5.3 A 300 MHz uniform plane wave propagates through fresh water for which σ = 0, μ_r =1 and ε_r = 78. Calculate : i) Attenuation constant, ii) Phase constant, iii) Wavelength, iv) Intrinsic impedance.
Sol. : i) For the given medium i.e. fresh water, conductivity σ = 0. Assuming medium to be a lossless medium, we can write,

attenuation constant ∝ = 0

ii) The phase constant is given by,

β = ω√με = ω√(μ₀ μ_r) (ε₀ ε_r)

Putting values of ω,μ₀,ε₀ and ε_r,

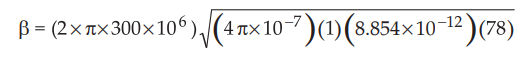
= 55.529 rad/m

iii) The wavelength is given by,

λ = 2π/ β = 2π/55.529 = 0.1131 m

iv) The intrinsic impedance is given by,

 

Ex. 10.5.4 A 6580 MHz uniform plane wave is propagating in a material medium of ε_r =2.25. If the amplitude is 500 V/m. Calculate the phase constant, lossless medium is 500 V/m. Calculate the phase constant, propagation constant, velocity, wavelength and intrinsic impedance. Also find the amplitude of the magnetic field intensity. AU: Dec.-1, Marks 13

Sol. :

Assume a lossless medium i.e. σ = 0

i) Phase constant, β = ω √με

β = 2πf √μ₀μ_rε₀ε_r

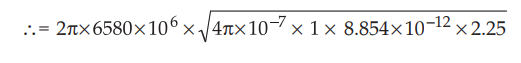
= 206.859 rad/m

ii) Propagation constant, ɤ = ɑ +jβ  but ɑ = 0

ɤ = j206.858 m^-1

iii) Phase velocity, v_p = ω/β =2πf/β

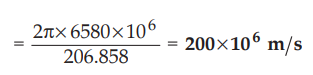
= 200 × 10^-6 m/s

iv) Wavelength λ = 2π/β =2π/206.858 = 0.03037m

b) Intrinsic impedance,

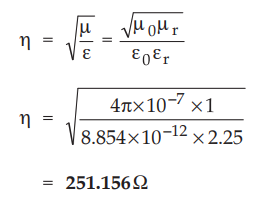
= 251.156 Ω

vi) Amplitude of the E is given as 500 V/m

          E_X = 500 V/m but η = E_x/H_y = 251.156

H_y  =500/251.156 = 1.99 A/m

This is amplitude of magnetic field intensity.

 

Ex. 10.5.5  A uniform plane wave propagating in a medium has 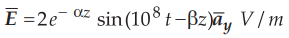 , If the medium is characterized by ε_r = 1, μ_r = 20 and σ = 3 S/m, fine ∝, β and H.

AU: May-04, 06, Dec.-15, Marks 8

Sol. :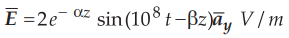 

Thus, E_m =2, ω= 10⁸ rad/sec

Let us check, the nature of medium. As σ≠0, the medium is not perfect dielectric.

= 3388.3 >> 1

Hence at ω = 10⁸ rad/sec the medium acts as good conductor.

For good conductor,

= √i(837.758) = 28.944 ∠ 45^o Ω

Now the wave propagates is +ve z-direction. But  is in  direction. So to achieve proper direction of wave propagation,  must be in p direction such that.

 

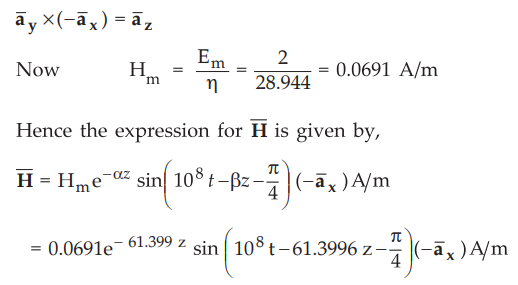
Ex. 10.5.6 Find the velocity of a plane wave in a lossless medium having a relatively permittivity of 5 and relative permeability of 1.

Sol. : For lossless medium, the velocity of plane wave is given by,

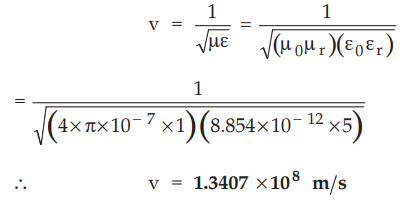
v = 1.3407 × 10⁸ m/s

 

Ex. 10.5.7 In a homogeneous region where μ_r = 1 and ε_r = 50, the fields are given as 

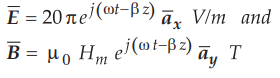
Find ω and H_m if the wavelength is 1.75 m.

Sol. : Assume lossless medium. σ = 0. The wavelength is given by,

λ = wπ/ β i.e. β = 2π/λ = 2π/1.75

= 3.59 rad/m

But for lossless medium,

β = ω √με = 3.59

But intrinsic impedance can also be expressed in terms of the magnitudes of electric and magnetic fields as,

Η = E_m / H_m

From the given expression of , the magnitude E_m is 20л.

Η_m = E_m / η = (20) (π) / 53.278 = 1.1793 A/m

 

Examples for Practice

Ex. 10.5.8 In a nonmagnetic medium

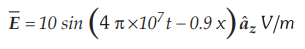
Find

a) Ɛr, η b) The time average power carried bp the wave

c) The total power crossing 100 cm² of plane 3x + y = 10.

Ex. 10.5.9 In certain medium  = 10 cos

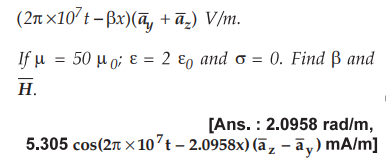
Ex. 10.5.10 The magnetic field component of a plane wave in a lossless dielectric is

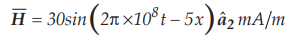
a) If µ_r =     1, find Ɛr.

b) Calculate the wavelength and wave velocity.

c) Determine the wave impedance.

d) Determine the polarization of the wave.

e) Find the corresponding electric field component.

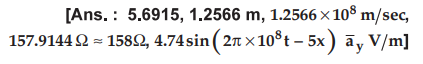
Review Questions

1. Explain propagation of uniform plane wave in perfect dielectric. What is lossless dielectric ?

2. Explain in detail the behaviour of plane waves in lossless medium.

3. Derive the expression for intrinsic impedance, propagation constant and velocity of a plane electromagnetic wave when propagated in a perfect dielectric medium.