Uniqueness Theorem

Uniqueness Theorem

• The boundary value problems can be solved by number of methods such as analytical, graphical, experimental etc. Thus there is a question that, is the solution of Laplace's equation solved by any method, unique? The answer to this question is the uniqueness theorem, which is proved by contradiction method.

• Assume that the Laplace's equation has two solutions say Vi and V2, both are function of the co-ordinates of the system used. These solutions must satisfy Laplace's equation. So we can write,

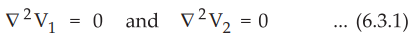
• Both the solutions must satisfy the boundary conditions as well. At the boundary, the potentials at different points are same due to equipotential surface then,

V₁ = V₂       ... (6.3.2)

• Let the difference between the two solutions is Vd.

V_d = V₂ – V₁         ... (6.3.3)

• Using Laplace’s equation for the difference X

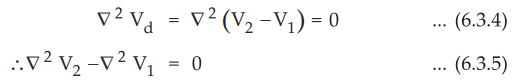
• On the boundary V_d = 0 from the equations (6.3.2) and (6.3.3).

• Now the divergence theorem states that,

• Now integration can be zero under two conditions, 

i) The quantity under integral sign is zero.

ii) The quantity is positive in some regions and negative in other regions by equal amount and hence zero.

• But square term cannot be negative in any region hence, quantity under integral must be zero.

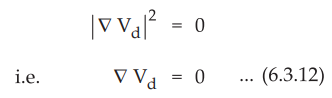
• As the gradient of V_d = V₂ – V₁ is zero means V₂ – V₁ is constant and not changing with any co-ordinates. But considering boundary it can be proved that V2 V₂ – V₁ = Constant = Zero.

V₂ – V₁... (6.3.13)

• This proves that both the solutions are equal and can not be different.

• Thus Uniqueness Theorem can be stated as :

• If the solution of Laplace's equation satisfies the boundary condition then that solution is unique, by whatever method it is obtained.

• The solution of Laplace's equation gives the field which is unique, satisfying the same boundary conditions, in a given region.

Review Question

1. State and explain uniqueness theorem.

AU : Dec.-14, Marks 8