Unsolved Problems with Answer

UNSOLVED PROBLEMS

 

1. A coil consists of 2000 turns of copper wire having a cross-sectional area of 0.8 mm². The mean length per turn is 80 cm, and the resistivity of copper is 0.2 μ Ω - m. Find the resistance of the coil.

[Ans: R= 40 Ω]

2. The resistance of a conductor 1 mm2 in cross-section and 20 m long is 0.346 Q. Determine the specific resistance of the conductor material.

[Ans: p = 1.73 × 10^-8 Ω-m]

3. Calculate the filament resistance in a (i) 100 W, 250 V lamp (ii) 1.5 kW, 250V iron.

[Ans: (i) 625 Ω (ii) 41.33 Ω]

4. A 20 Ω resistor is connected in series with an unknown resistor to a 200V supply. If the current drawn in 4A, find the value of the unknown resistor and power in each resistor.

[Ans: 30 Ω, 320 W, 480 W]

5. Two coils connected in parallel across 100V supply draw a total current of 9A. The power dissipated in one coil is 500W. Find the resistance of the two coils.

[Ans: 20 Ω, 25 Ω]

6. A resistor, R is connected in series with a parallel combination of two resistances of 12 2 and 6 2. This circuit takes 150W power from a supply of 30V. Calculate the value of R.

[Ans: R = 2 Ω]

7. A filament lamp is rated 100W and 110V. Find the value of the resistance to be connected in series with this lamp so that it can be operated on a 230V supply. What is the power loss in the resistor?

[Ans: R= 132 Ω; P= 109.1 W]

8. Across a 230V supply terminals in a house, an electric iron having a resistance of 50 Ω and incandescent lamps of resistances 450 Ω and 800 Ω respectively are connected. Find the total current and power taken from the supply mains.

[Ans: I= 5.163 A; P = 1135.86 W]

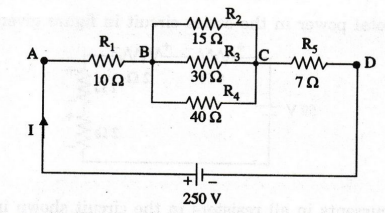
9. In the circuit shown in figure, find the current in the 40 Ω resistor.

[Ans: 2A]

10. What is the current in the circuit shown in figure? Determine the voltage across each resistor.

[Ans: I = 2 μA, V₁ M = 2 V, V_{3.1 M} = 6.2 V V_{400 k} = 0.8 V, V_{500 k} = 1 V]

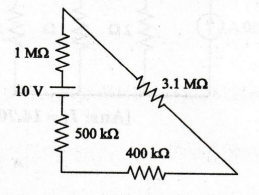
11. In the circuit given in figure, find (a) the current I, and (b) the voltage across 30 Ω

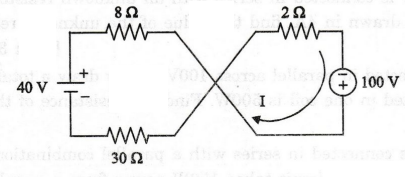
 [Ans: I = 1.5 A, V_{30 Ω =} 45 V]

12. What is the voltage across the 10 Ω resistor in figure given below.

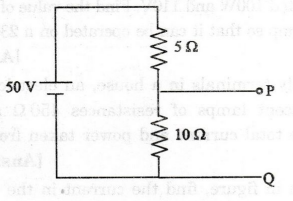
[Ans: 33.3 V]

 

13. Determine the total power in the series circuit in figure given below.

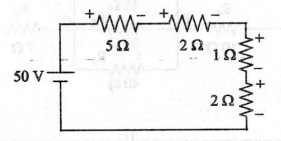
 [Ans: 250 W]

14. Determine the currents in all resistors in the circuit shown in figure.

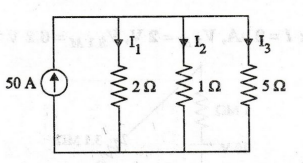
 [Ans: I₁ = 14.705 A, I₂ = 29.41 A, I₃ = 5.88 A]

15. For the circuit shown in figure, find the voltage across the 10 2 resistor and the current passing through it.

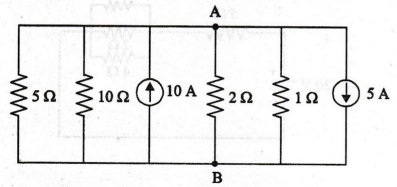
 [Ans: V₁₀ = 2.78 V, I₁₀ = 0.278 A]

16. Determine the current through resistance R₃ in the circuit shown in figure.

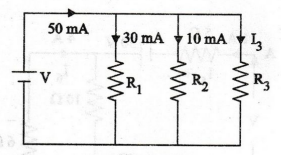
 [Ans: I₃ = 10 mA]

17. Determine the equivalent resistance between points C and D of the circuit shown in figure.

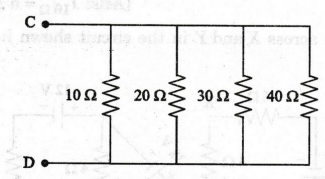
[Ans: 4.8 Ω]

18. Determine the current through each resistor in the circuit shown in figure.

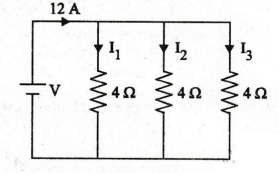
 [Ans: I1 = 4 A, I₂ = 4 A, I₃ = 4A]

19. Determine the current in the circuit shown in figure.

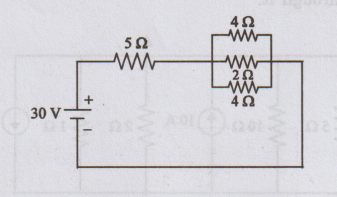
[Ans: 5A]

 

20. Find the current in the 10 Ω resistance, V₁ and source V in the circuit shown in figure.

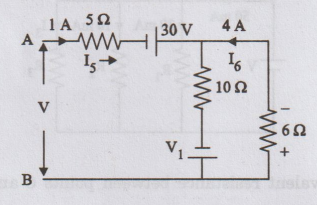
[And: I_{10 Ω} = 5A, V₁ = 74V, V = 149 V]

 

21. What is the voltage across X and Y in the circuit shown in figure?

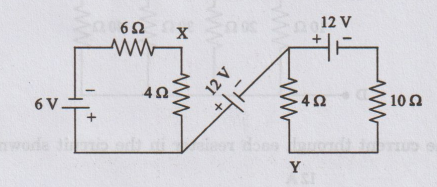
[Ans: V_XY = 13.04 V]

 

22. Determine the current delivered by the source in the circuit shown in figure.

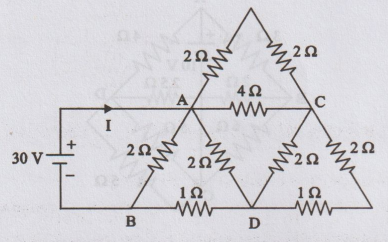
 [Ans: I = 28.57 A]

23. Determine the current in the 10 2 resistance and find voltage across A and B in the circuit shown in figure.

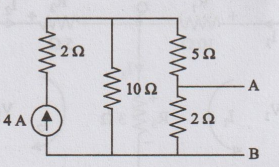
 [Ans: I₁₀ = 1.65 A, V_AB = 4.7 V]

24. Determine the value of resistance R and current in each branch when the total current taken by the circuit shown in figure is 6A.

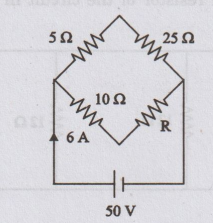
 [Ans: I₃₀ = 1.66 A, I₁₀+ R = 4.34 A, R = 1.52 Ω]

25. Find the power delivered by the source in the circuit shown in figure.

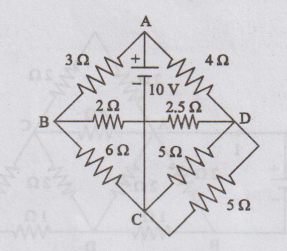
 [Ans: 41.3 W]

26. Assuming the internal resistance of the batteries to be zero, calculate the current supplied by the two batteries in the network shown in figure.

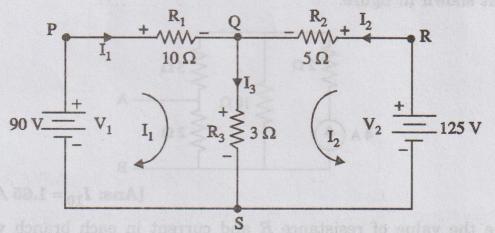
 [Ans: I₁ = -1A, I₂ = 5 A]

27. Find the current in the load resistor of the circuit in figure.

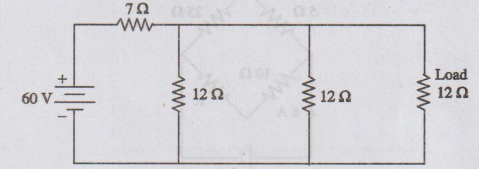
 [Ans: 1.818 A]

28. For the circuit in figure, find the load current and power.

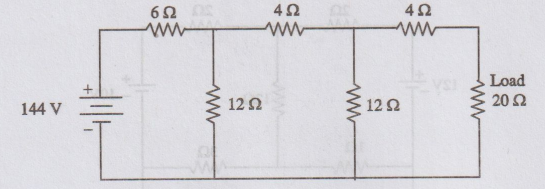
 [Ans: 2A, 80W]

29. In the network shown in figure, find the magnitude and direction of each branch A current by mesh current method.

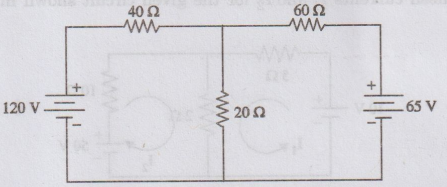
[Ans: I₁ = 1.886 A; I₂ = 0.341 A]

30. Calculate the current in each branch of the circuit shown in figure.

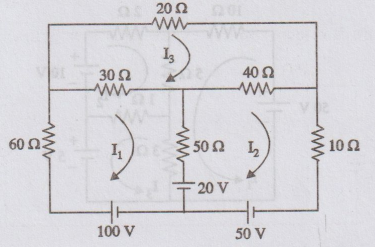
 [Ans: I₁ = 1.65 A, I₂ = 2.16 A; I₃ = 1.5 A]

31. Determine the current in the 4 2 branch in the circuit shown in figure.

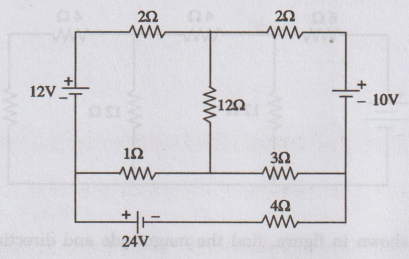
 [Ans: 4.11 A]

32. Determine mesh currents I1 and I2 for the given circuit shown in figure.

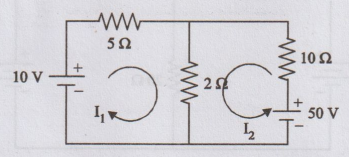
[Ans: I₁ = 0.25 A, I₂ = 4.125 A]

33. Determine the mesh current I1 in the circuit shown in figure.

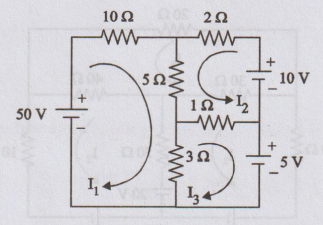
[Ans: I₁ = 3.3 A]

34. Write the node voltage equations and determine the currents in each branch for the network shown in figure.

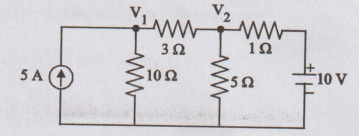
[Ans: V₁ = 19.85 V, V₂ = 10.9 V, I₁₀ = 1.985 A I₃ = 2.98 A, I₅ = 2.18 A, I₁ = 0.9 A]

35. Determine the voltages at each node for the circuit shown in figure.

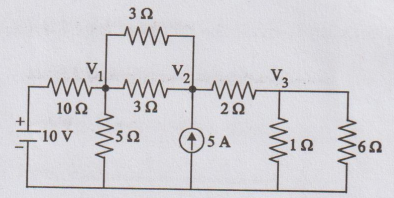
 [Ans: V₁ = 8.06 V, V₂ = 10.2 V, V₃ = 3.07 V]

36. Obtain the star connected equivalent for the delta connected circuit shown in figure

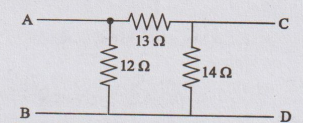
 [Ans: 4Ω,4.66 Ω, 4.31 Ω]

37. Obtain delta-connected equivalent for the star-connected circuit shown in figure.

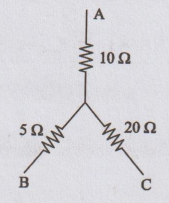
 [Ans: 17.5Ω, 35 Ω, 70Ω]