Vector Algebra

Vector Algebra

• The various mathematical operations such as addition, subtraction, multiplication etc. can be performed with the vectors. In this section the following mathematical operations with the vectors are discussed.

1. Scaling 2. Addition 3. Subtraction.

1. Scaling of vector

• This is nothing but, multiplication by a scalar to a vector. When a scalar is positive then such a multiplication changes the magnitude (length) of a vector but not its direction.

• Let α = Scalar with which vector is to be multiplied

• Then if α >1 then after multiplying to a vector the magnitude of a vector increases but direction remains same. If α <1 then after multiplying to a vector the magnitude of a vector decreases but direction remains same.

• If α = -1 then after multiplying to a vector the magnitude of vector remains same but direction of the vector reverses.

Key Point : Thus if a is negative, the magnitude of vector changes by a times while the direction becomes exactly opposite to the original vector, after multiplication.

2. Addition of Vectors

• Consider two coplanar vectors as shown in thw Fig. 1.4.1. The vectors which lie in the same plane are calles Coplanar vectors.

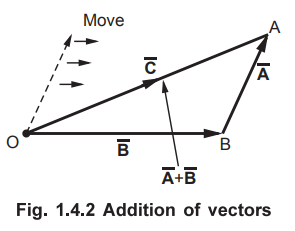
• Let us find the sun of these two vectors 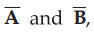 shown in the Fig. 1.4.1.

• The procedure is to move one of the two vectors parallel to itself at the tip of the other vector. Thus move  , parallel to itself at the tip of 

• Then join tip of moved, to the origin. This vector represents resultant which is the addition of the two vectors  and . This is shown in the Fig. 1.4.2.

• Let us denote this resultant as  then

• It must be remembered that the direction of  is from origin O to the tip of the vector moved.

• Another point which can be noticed that if  is moved parallel to itself at the tip of , we get the same resultant  Thus, the order of the addition is not important. The addition of vectors obeys the commutative law i.e. .

• Another method of performing the addition of vectors is the parallelogram rule. Complete the parallelogram as shown in the Fig. 1.4.3. Then the diagonal of the parallelogram represents the addition of the two vectors. 

• Once the co-ordinate systems are defined, then the vectors can be expressed in terms of the components along the axes of the co-ordinate system. Then by adding the corresponding components of the vectors, the components of the resultant vector which is addition of the vectors, can be obtained. This method is explained after the co-ordinate systems are discaussed.

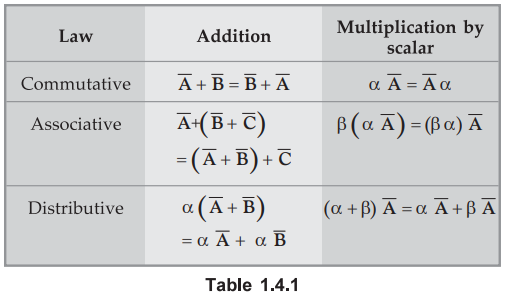
• The following basic laws of algebra are obeyed by the vectors :

• In this table α and β are the scalars i.e. constants.

3. Subtraction of Vectors

• The subtraction of vectors can be obtained from the rules of addition. If  is to be subtracted from   then based on addition it can be represented as,

• Thus reverse the sign of  i.e. reverse its direction by multiplying it with -1 and then add it to  to obtain the subtraction. This is shown in the Fig. 1.4.4 (a) and (b).

a. Identical Vectors

•  Two vectors are said to be identical if there difference is zero. Thus 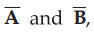are identical if . Such two vectors are also called equal vectors.