Vector or Cross Product of Vectors

Vector or Cross Product of Vectors

AU : May-07

• Consider the two vectors 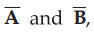  the cross product is denoted as  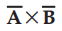and defined as the product of the magnitudes of 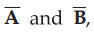  and the sine of the smaller angle between  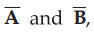. But this product is a vector quantity and has a direction perpendicular to the plane containing the two vectors 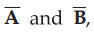 . But for any plane there are two perpendicular directions, upwards and downwards. To avoid the confusion, the direction of the cross product is along the perpendicular direction to the plane which is in the direction of advancement of a right handed screw when    is turned into  . Thus right hand screw rule decides the direction of the cross product.

• Mathematically the cross product is expressed as,

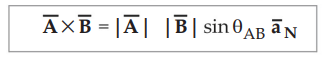        ...(1.11.1)

where  = Unit vector perpendicular to the plane of  and  in the direction decided by the right hand screw rule.

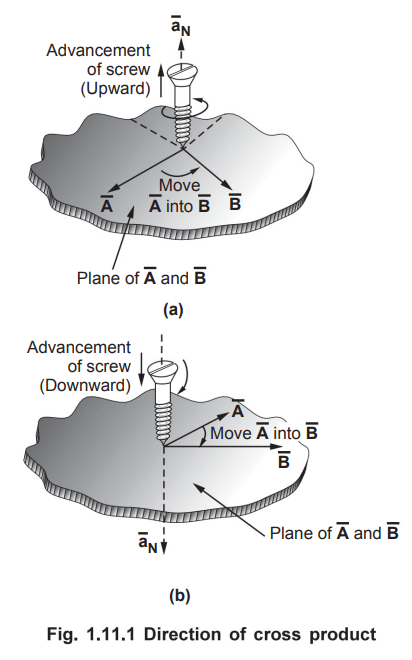
The concept of  is shown in the Fig. 1.11.1.

1. Properties of Cross Product

• The various properties of cross product are,

1. The commutative law is not applicable to the cross product. Thus,

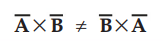... (1.11.2) 

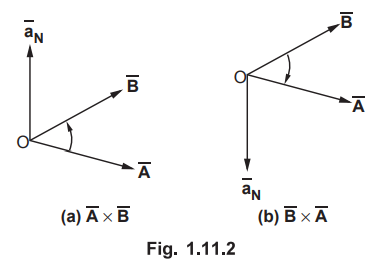
• Consider the two vectors as shown in the Fig. 1.11.2 (a). Then 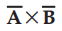 gives unit vector  in the upward direction. But if 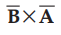 is obtained then direction of   must be determined by rotating   into   which results into downward direction. This is shown in the Fig. 1.11.2 (b).

• Hence cross product is not commutative.

2. Reversing the order of the vectors 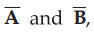 a unit vector   reverses its direction hence we can write,

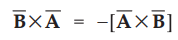... (1.11.3)

• It is anticommutative in nature.

• If order of cross product is changed, the magnitude remains same, but direction gets reversed.

3. The cross product is not associative. Thus,

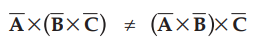  ... (1.11.4)

• 4. With respect to addition the cross product is distributive. Thus,

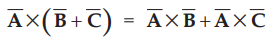...(1.11.5)

5. If the two vectors are parallel to each other i.e. they are in the same direction then 0 = 0° and hence cross product of such two vectors is zero.

• Thus if cross product of the two vectors is zero then those two vectors are parallel i.e. are in the same direction, assuming none of the two vectors itself is zero.

6. If the cross product of a vector  with itself is calculated, it is zero as θ = 0°

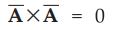.. (1.11.6)

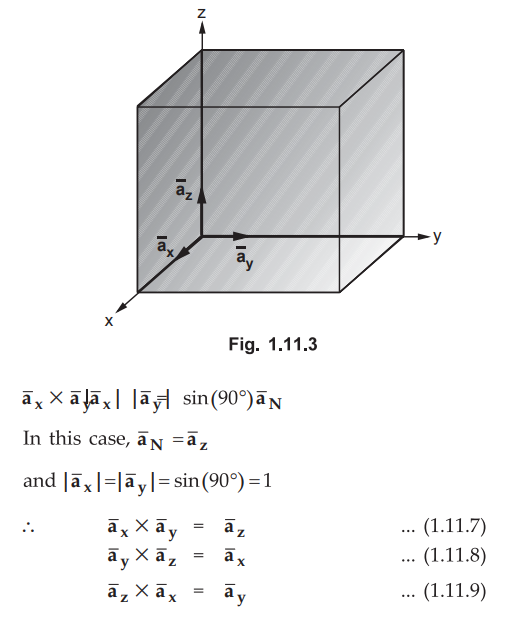
7. Cross product of unit vectors : Consider the unit vectors 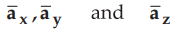 which are mutually perpendicular to each other, as shown in the Fig. 1.11.3.

• But if the order of unit vectors is reversed, the result is negative of the remaining third unit vector. Thus,

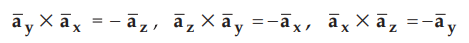... (1.11.10)

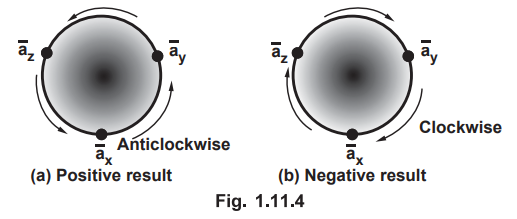
• This can be remembered by a circle indicating cyclic permutations of cross products of unit vectors as shown in the Fig. 1.11.4.

• While as cross product of vector with itself is zero

we can write,

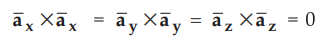... (1.11.11)

• The result is applicable for the unit vectors in the remaining two co-ordinate systems.

• From the Fig. 1.11.5 we can write,

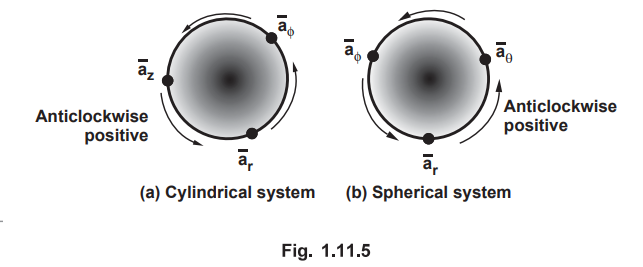
 Key Point : The clockwise direction gives negative result.

8. Cross product in determinant form : Consider the two vectors in the cartesian system as,

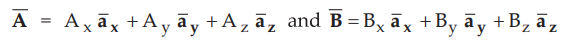
• Then the cross product of the two vectors is,

2. Applications of Cross Product

• The different applications of cross product are,

1. The cross product is the replacement to the right hand rule used in electrical engineering to determine the direction of force experienced by current carrying conductor placed in a magnetic field.

• Thus if I is the current flowing through conductor while  is the vector length considered to indicate the direction of current through the conductor. The uniform magnetic flux density is denoted by vector  Then the force experienced by conductor is given by,

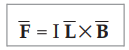
2. Another physical quantity which can be represented by cross product is moment of a force. The moment of a force (or torque) acting on a rigid body, which can rotate about an axis perpendicular to a plane containing the force is defined to be the magnitude of the force multiplied by the perpendicular distance from the force to the axis. This is shown in the Fig. 1.11.6.

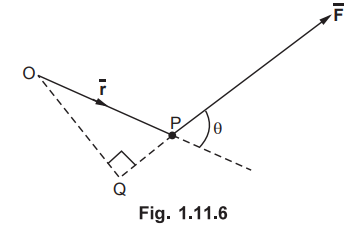
• The moment of force 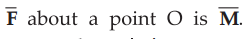. Its magnitude is  sin θ where   sin θ is the perpendicular distance of from O i.e. OQ.

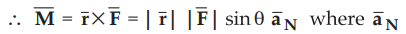.•  is the unit vector indicating direction of which is perpendicular to the plane i.e. paper and coming out of paper according to right hand screw rule.

Ex. 1.11.1 If two vectors are expressed in cylindrical co-ordinates as

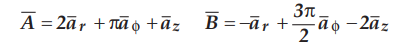Compute a unit vector perpendicular to the plane containing A and B. AU : May-07, Marks 6

Sol. :

The Perpendicular vector to the plane containing 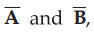  is given by their cross product.

Examples for Practice

Review Question

1. Define cross product of vectors. State its properties and applications.