Wien Bridge Oscillator using Op-amp

Wien Bridge Oscillator

Generally in an oscillator, amplifier stage introduces 180° phase shift and feedback network introduces additional 180° phase shift, to obtain a phase shift of 3609 (2TI radians) around a loop. This is required condition for any oscillator. But Wien bridge oscillator uses a noninverting amplifier and hence does not provide any phase shift during amplifier stage. As total phase shift required is 0° or 2 nn radians, in Wien bridge type no phase shift is necessary through feedback. Thus the total phase shift around a loop is 0°. Let us study the basic version of the Wien bridge oscillator and its analysis.

A basic Wien bridge used in this oscillator and an amplifier stage is shown in the Fig. 3.18.1.

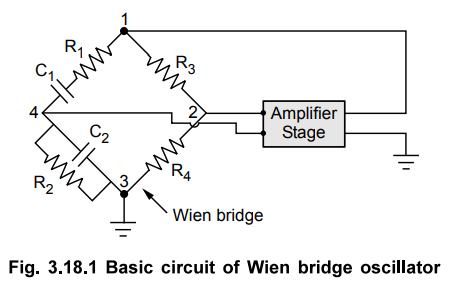
The output of the amplifier is applied between the terminals 1 and 3, which is the input to the feedback network. While Fig. 3.18.1 Basic circuit of Wien bridge oscillator the amplifier input is supplied from the diagonal terminals 2 and 4, which is the output from the feedback network. Thus amplifier supplied its own input through the Wien bridge as a feedback network.

The two arms of the bridge, namely R₁ C₁ in series and R₂, C₂ in parallel are called frequency sensitive arms. This is because the components of these two arms decide the frequency of the oscillator. Let us find out the gain of the feedback network. As seen earlier input to the feedback network is between is 1 and 3 while output V_f of the feedback network is between 2 and 4. This is shown in the Fig. 3.18.2. Such a feedback network is called lead-lag network. This is because at very low frequencies it acts like a lead while at very high frequencies it acts like lag network.

Now from the Fig. 3.18.2, as shown,

This is the frequency of the oscillator and it shows that the components of the frequency sensitive arms are the deciding factors, for the frequency.

In practice, R₁ = R₂ = R and C₁ = C₂ = C are selected.

We get the magnitude of the feedback network at the resonating frequency of the oscillator as,

The positive sign of β indicates that the phase shift by the feedback network is 0°. Now to satisfy the Barkhausen criterion for the sustained oscillations, we can write,

Another important advantage of the Wien bridge oscillator is that by varying the two capacitor values simultaneously, by mounting them on the common shaft, different frequency ranges can be provided.

1. Wien Bridge Oscillator using Op-amp

The Fig. 3.18.4 shows the Wien bridge oscillator using an op-amp.

The resistance R and capacitor C are the components of frequency sensitive arms of the bridge. The resistance R and R₁ form the part of the feedback path. The gain of noninverting op-amp can be adjusted using the resistance R and R₁. The gain of op-amp is,

A = 1 + R_f / R₁

To satisfy Barkhausen criterion that Aβ ≥ 1 it is necessary that the gain of the noninverting op-amp amplifier must be minimum 3.

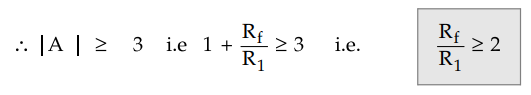
Thus ratio of R_f and R₁ must be greater than or equal to 2.

The frequency of oscillations is given by,

The feedback is given to the noninverting terminal of op-amp which ensures zero phase shift. It is used popularly in laboratory signal generators.

If in a Wien bridge feedback network, two resistances are not equal i.e. they are R₁ and R₂ while two capacitors are not equal i.e. they are C₁ and C₂ then the frequency of oscillations is given by,

With R₁ = R₂ = R and C₁ = C₂ = C we get it as l/2π RC as stated earlier.

The simplified circuit diagram of the Wien bridge oscillator is shown in the Fig. 3.18.5.

2. Advantages

The various advantages of Wien bridge oscillator are,

1. By varying the two capacitor values simultaneously, by mounting them on the common shaft, different frequency ranges can be obtained.

2. The perfect sine wave output is possible.

3.  It is useful audio frequency range i.e. 20 Hz to 100 kHz. 

3. Wien Bridge Oscillators Design

Select the capacitor value much larger than the stray capacitance, about 0.01 to 0.05 μF. From the equation of frequency, obtain the value of R.

R = 1 / 2π fC

Then for noninverting amplifier,

R_f = 2 R₁

Choose R₁ and design the value of R_f. Keep R_f variable for fine adjustments.

Example 3.18.1 Design the Wien bridge oscillator circuit to have output frequency of 5 kHz.

May-18, Marks 4

Solution : Choose C = 0.01 µF 

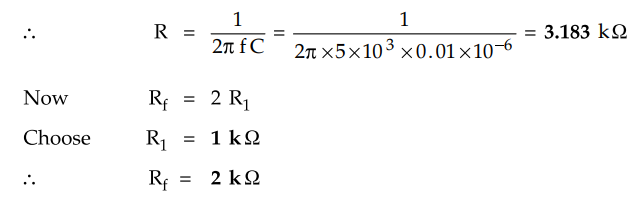
Use standard value of 2.2 k2 to have A_CL > 3. The designed circuit is shown in the Fig. 3.18.6.

Review Question

1. Draw the circuit of a Wien bridge oscillator using op-amp and derive an expression for its frequency of oscillation. May-04, Marks 8

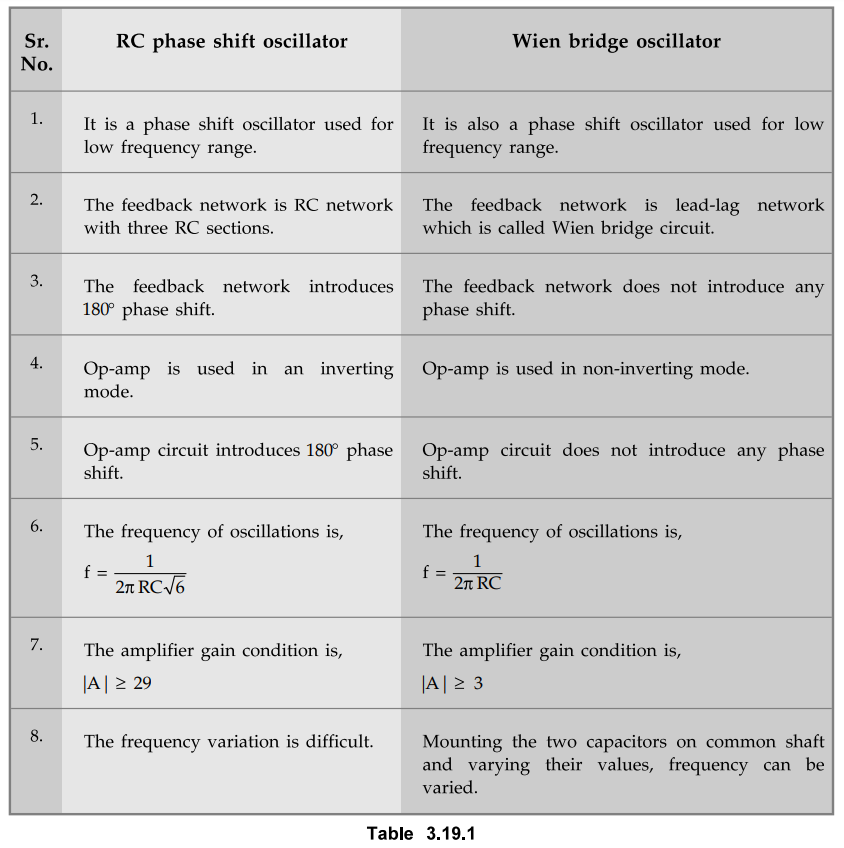
Comparison of RC Phase Shift and Wien Bridge Oscillators

The similarities and the difference between the two oscillators are given in the table 3.19.1