Work Done

Work Done

• The electric field intensity is defined as the force on a unit test charge at that point at which we want to find the value of  . Consider an electric field due to a positive charge Q. If a unit test positive charge Q_t is placed at any point in this field, it experiences a repulsive force and tends to move in the direction of the force.

• But if a positive test charge Q_t is to be moved towards the positive base charge Q then it is required to be moved against the electric field of the charge Q. i.e. against the repulsive force exerted by charge Q on the test charge Q_t. While doing so, an external source has to do work to move the test charge Qt against the electric field. This movement of charge requires to expend the energy. This work done becomes the potential energy of the test charge Q_t, at the point at which it is moved.

• Consider an earth's gravitational field. An object falls on the earth due to the force exerted by earth's gavitational field. But to move an object away from the earth's gravitational field, the work is required to be done by an external source. The force in opposite direction to that exerted by earth's gravitational field is required to be applied, to move an object against the earth's gravitational field. In such a case, work is said to be done.

• Thus, work is said to be done when the test charge is moved against the electric field.

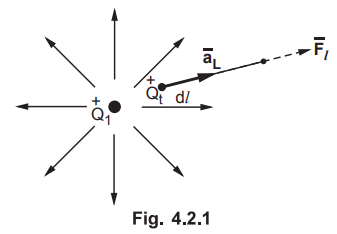
• Consider a positive charge Q₁ and its electric field   If a positive test charge Q_t is placed in this field, it will move due to the force of repulsion. Let the movement of the charge Q_t is dl. The direction in which the movement has taken place is denoted by unit vector , in the direction of dl. This is shown Fig. 4.2.1

• According to Coulomb's law the force exerted by the field   is given by,

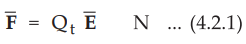
• But the component of this force exerted by the field in the direction of dl, is responsible to move the charge Q_t, through the distance dl.

• We know that the component of a vector in the direction of the unit vector is the dot product of the vector with that unit vector. Thus the component of  in the direction of unit vector  is given by,

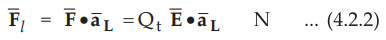
• This is the force responsible to move the charge Qt through the distance dZ, in the direction of the field.

• To keep the charge in equilibrium, it is necessary to apply the force which is equal and opposite to the force exerted by the field in the direction dl.

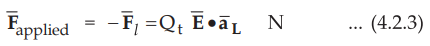
• In this case, the work is said to be done.

Key Point : Thus keeping the charge in equilibrium means we are moving a charge Q_t, through the distance dl in opposite direction to that of field  . Hence the work is done.

• Thus there is expenditure of energy which is given by the product of force and the distance.

• Hence mathematically the differential work done by an external source in moving the charge Q_t through a distance dl, against the direction of field   is given by,

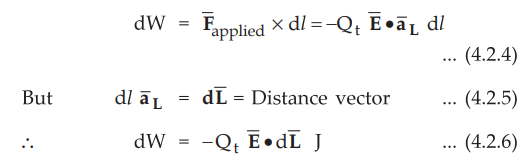
Key Point : Note that dW is a scalar quantity as 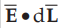 is the dot product which is a scalar quantity.

• Thus if a charge Q is moved from initial position to the final position, against the direction of electric field   then the total work done is obtained by integrating the differential work done over the distance from initial position to the final position.

The work done is measured in Joules.

Key Point : Note that at both the positions initial and final, the charge Q is at rest and not moving, then only the equation (4.2.7) is valid.

Review Question

1. Define a work done and obtain the line integral to calculate the work done in moving a point charge Q in an electric field  .

AU : May-05, 10, 19, Dec.-19