Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Worked examples: AC circuits by nodal analysis
Electric Circuit Analysis: Unit I: Basic circuits analysis : Worked examples
WORKED EXAMPLES
AC CIRCUITS BY NODAL
ANALYSIS
Example
13 Determine the real power output of the source in the circuit shown in
figure, by nodal analysis and verify the results by using loop analysis.
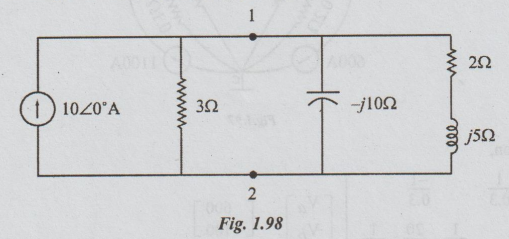
Solution:
Nodal Method
There are two nodes 1 and 2. Let the node 2 be the reference one. Then applying KCL at node 1 we get the following equation:
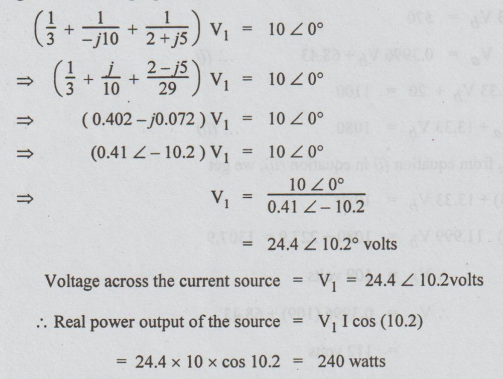
Loop Current Method :
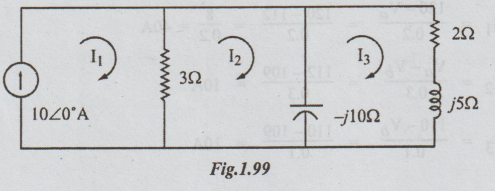
Let
the loop currents be as shown
I1=10A....(i)
Applying
KVL to loop 2, we get
It
is the same answer as in the nodal method. Thus the solution is verified.
Example
14 In the network shown in figure, find the node voltages V1 and V2.
Find also the current supplied by the source.
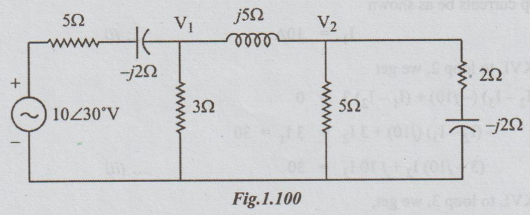
Solution:
The above circuit is re-drawn as below after converting the voltage source into
its equivalent current source.
Example
15 Using nodal analysis, find the current through the 4 ohm resistor in the
circuit shown in figure.
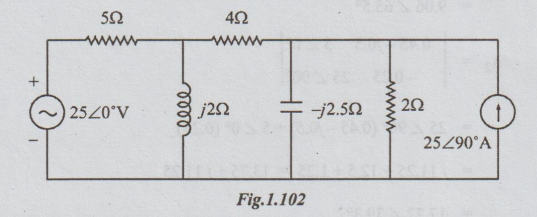
Solution:
The voltage source is converted into its equivalent current source and the
network is drawn below:
V1
= Δ1/Δ = 9.06 ∠
65.5° / 0.513 ∠ 22.3°
=
17.66 ∠Δ 87.8° volts
= (0.677 + j17.6) volts
V2
= Δ2/Δ = 17.77 ∠
39.3° / 0.513 ∠ 22.3°
=
34.64 ∠ 61.6° volts
=
(16.47+ j30.47) volts
Voltage across 4Ω = V2 - V1
=
(16.47 + j30.47) - (0.677 + j17.6)
=
(15.793 + j12.87)
=
20.37 ∠ 39.17° volts
Current through 4 Ω = 20.37 ∠39.17o / 4
=
5.0925 ∠ 39.17°A
This
current flows from node 2 to node 1.
Example
16 Given the nodes 1 and 2 in network of figure find the ratio of node voltage V1/V2
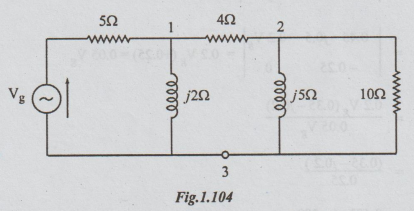
Solution:
The network is re-drawn as below after converting the voltage source into
current source:
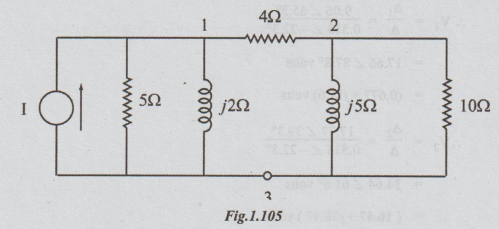
Putting
in the matrix form, we get
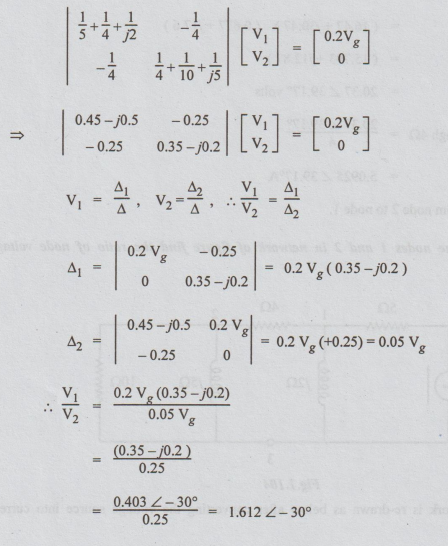
V1
/ V2 = 0.2 Vg
(0.35 – j0.2) / 0.05vg
=(0.35
- j0.2) / 0.25
=
(0.35 - j0.2) / 0.25
=
0.403 ∠ -30° / 0.25
= 1.612 ∠ -30°
Electric Circuit Analysis: Unit I: b. Basic circuits analysis : Tag: : - Worked examples: AC circuits by nodal analysis
Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation