Electric Circuit Analysis: Unit I: b. Basic circuits analysis
Worked examples: Loop (mesh) current method
Electric Circuit Analysis: Unit I: Basic circuits analysis : Worked examples
WORKED
EXAMPLES
Example
1 Write the mesh equations for the circuit shown in the figure and solve for
the current in the 12Ω resistor.
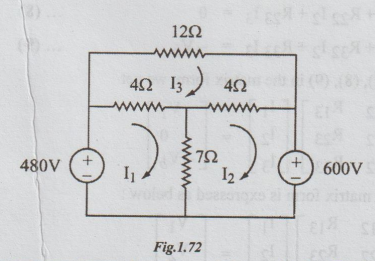
Solution:
The loop currents are assumed as shown. It is required to find i3. By
inspection we can write,
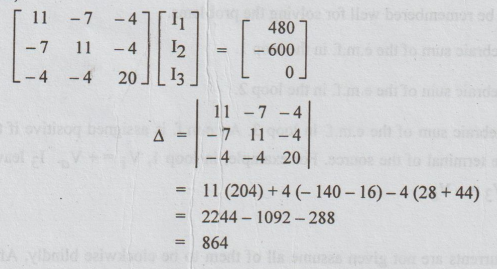
=
11 (204) + 4(-140-16) -4 (28 + 44)
=
2244 – 1092 - 288
=
864

=
480 (72) + 600 (-44-28)
=
- 8640
I3=
Δ3/Δ = - 8640 / 864
=
- 10A
(-) indicates that the assumed direction of I3
is not the actual direction I3 The actual direction of I3 is
anti-clockwise. i.e., the current through 12 Ω is 10A flowing from the right to
the left terminal of the resistor.
Example
2 Write and solve the equations for the mesh currents in the network in figure.
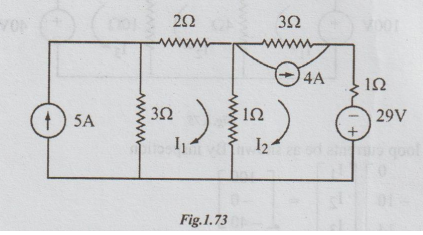
Solution:
For solving the problems on the mesh current (loop current) method, the
preferable method is to convert the practical current sources into practical
voltage sources.
The
original circuit is redrawn as in the figure below after transforming the
current sources into voltage sources.
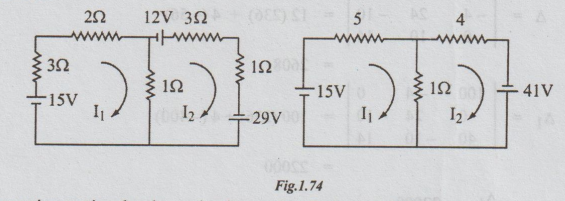
By
Inspection putting the above circuit equations in the matrix form,

I1
= Δ1/ Δ =116/29 = 4A
I2
= Δ2/ Δ = 261/29 = 9A
Example
3 Write the mesh equations for the network shown in figure by inspection and
find the power absorbed by 8 Ω resistor.
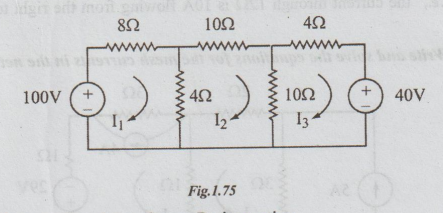
Solution:
Let
the loop currents be as shown. By inspection
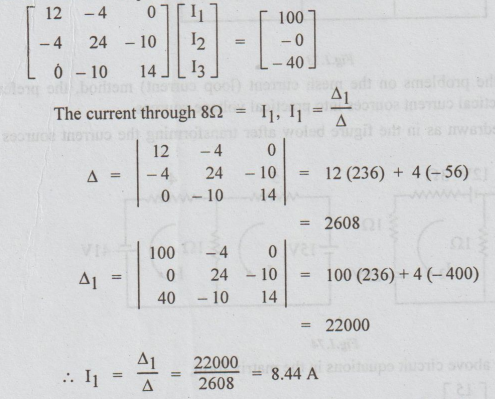
Power
absorbed by 8 Ω resistor VI = 100 × 8.44 8.44 W
The
mesh equations are as expressed below:
I2
I1 - 4 I2 = 100
....(i)
-4I1
+ 24 I2-10 I3 = 0 ...(ii)
-
10 I2 + 14 I3 = -40... (iii)
Example
4 Write the mesh equations for the network shown in figure below by inspection
and find the power absorbed by the 3-ohm resistor.
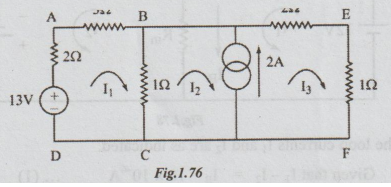
Solution:
Applying KVL to the mesh ABCD, we get
-5I1-(I1-I2)
1 + I3 =0
⇒ 6I1-I2
= 13....(i)
Aapplying
KVL to the mesh BEFC,
-3I3-(I2-I1)
1 = 0
⇒ I1-I2-3I3
= 0 ... (ii)
The
source current is given by
(I3-I2)
= 2 ... (iii)
Multiplying
(iii) by 3 and adding to (ii)
I1-4I2
= 6....(iv)
Multiplying
(i) by 4 and subtracting from (iv)
23
I1 =46
I1= 2A
Therefore,
the power observed in 3 Ω resistor
=
I12 × 3 = 22 × 3 = 12 watt
Example
5 In the Circuit shown in the figure, IB = 10 μA. Find the value of resistance
Rin

Solution:
Step
1: The given circuit can be drawn as below.
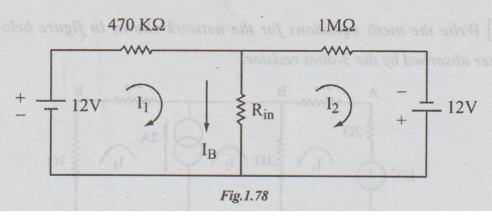
Step
2: Assume
that the loop currents I, and I2 are as indicated.
Step
3:
Given
that I1-I2= IB = 10 x 10-6 A... (1)
Applying
KVL to the left loop, we get
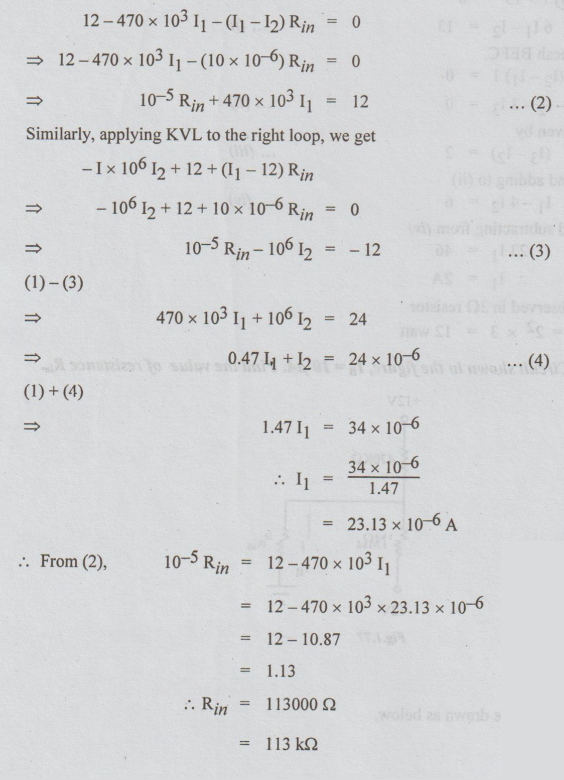
Electric Circuit Analysis: Unit I: b. Basic circuits analysis : Tag: : - Worked examples: Loop (mesh) current method
Related Topics
Related Subjects
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
