Electric Circuit Analysis: Unit III: Transient Response Analysis
D.C. Transients in RL Circuit
Worked Example Solved Problems
Electric Circuit Analysis: Unit III: Transient Response Analysis : Worked examples
WORKED EXAMPLES
D.C. Transients in RL Circuit
Example
1 A d.c. voltage of 100 volts is applied to a series RL circuit with R = 252
What will be the current in the circuit at twice the time constant?
Solution:
As the voltage source is in the circuit, the expression for rise in current is
given by

Example
2 Sketch the current given by i (t) = 5 - 4e-20t.
Solution:
i
= 5 - 4e-20t
=
4 [ 1.25 - e-20t]
Let
us assume that t take some values like t = 0, 0.1 sec, 0.15 sec, 0.2 sec, 0.25
sec. For these values of t, i is calculated and the result is tabulated for
convenience.
The
sketch is drawn in fig. 3.8.

Example
3 In the circuit of the fig. 3.8, find the expression for the transient current
and the initial rate of growth of the transient current.
p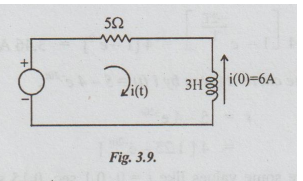
Solution:
By applying KVL, we get
5i
+ 3 di / dt = 100 u (t) ... (i)
As
i (0) is directed opposite to that of i (t), i (0) is treated as negative. That
is i (0) = -6. Taking Laplace Transformation of equation (i),

Taking
inverse Laplace Transformation, on both sides,
i
(t) = 20 - 26 e-5t/ 3
To
find the initial rate of growth of i.
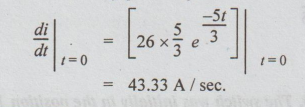
Example
4 In the circuit shown in the fig. 3.9, switch S is in position 1 for a long
time and brought to position 2 at time t = 0. Determine the circuit current.
Solution:
After closing the switch to the position 2 applying KVL, we get
5i
+ 2 di / dt = 10 ... (i)
Taking
Laplace Transformation on both sides,
51
(s) + 2 {s I (s)- i (0+) } = 10 / s … (ii)
i
(0+) is the current passing through the circuit just after the switch is at
position 2. Since the inductor does not allow sudden changes in currents, this
currents is equal to the steady state current when the switch was in position 1
[Because switch was in position 1 for long time.]
i (0+) = 50 / 5 = 10 A
Substituting
this in equation (ii),
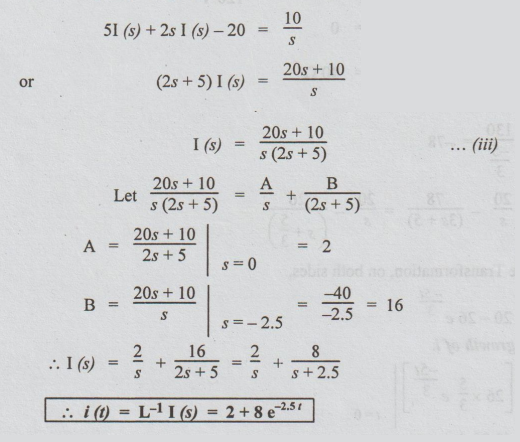
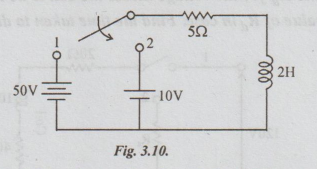
Example
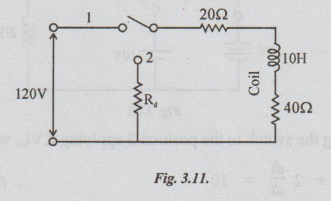
5 In the circuit shown in fig. 3.10. The switch was initially in the position
1. (a) for Ra =500 Ω find the voltage across the coil the instant at which the
switch is changed to position 2. (b) Calculate the value of the Ra for the
voltage across the coil to be reduced to 120 V at the instant of switching. (c)
with the value of Rain case. Find the time taken to dissipate 95% of stored
energy.
Solution:
(a)
Steady current with the switch in position 1 = 120 / 20 + 40 = 2A.
Now,
with Rd = 500 and the switch changed to position 2, applying
Kirchoff's voltage law, we get the following equation.
2
× 500 + 2 × 20 + voltage across the coil = 0 ... (i)
⇒ Voltage across the coil
= - 1040 V
[-sign
indicates that the voltage is in opposite direction.]
(b)
In this case, the voltage across the coil = 120 V
Therefore,
Rd × 2 + 2 × 20 -120 = 0
⇒ Rd = 80 / 2 =
40 Ω
(c)
Energy stored = 1/2 LI2
Energy
stored = 1/2 × 10 × 22 = 20 joule
Given
that, 95% of energy is dissipated. So, residual energy = 5% of energy stored =
0.05 × 20 = 1 joule.
Let
i be the current at that instant. Then,
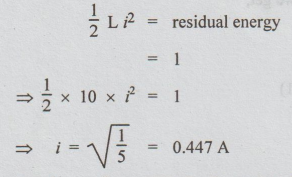
This
case is a decay of current in R-L combination.
The
equation for i is given by,
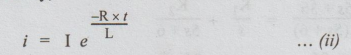
Here
I = 2A, R = 40 + 40 + 20 = 100 Ω
L
= 10 H
Substituting
these values in (ii), we get,
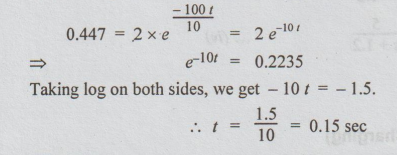
Example
6 Find the current in the circuit shown in fig.3.12, at an instant t, after
opening the switch if a current of 1 amp. had been passing through the circuit
at the instant of opening.
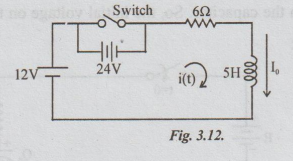
Solution:
After
t seconds of opening the switch, applying KVL, we get,
iR
+ L di / dt = E ... (i)
Here
R = 6Ω, L = 5H, E = the total voltage of the circuit after opening the switch =
12 + 24 = 36V
Given
that I0+ = Initial current = 1A
Putting
the values of R, L and E in (i), we get,
6i
+ 5dt/dt = 36 …. (ii)
Taking
Laplace transformation on both sides, we get,
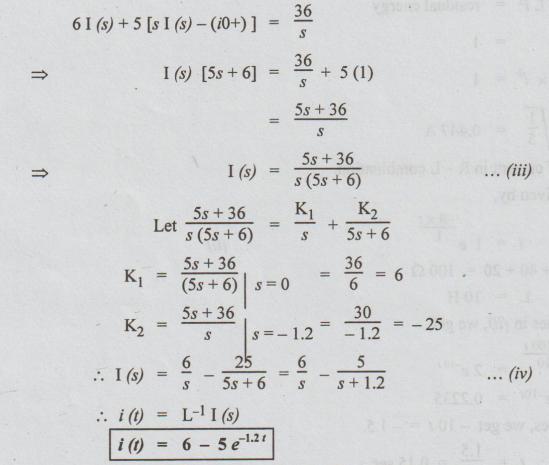
Electric Circuit Analysis: Unit III: Transient Response Analysis : Tag: : Worked Example Solved Problems - D.C. Transients in RL Circuit
Related Topics
Related Subjects
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
